1.2.1 几个常见函数的导数课件18张PPT
文档属性
| 名称 | 1.2.1 几个常见函数的导数课件18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 258.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 00:00:00 | ||
图片预览





文档简介
课件18张PPT。1.2.1几个常见函数的导数
高中人教A版选修《数学2-2》一、复习导数的几何意义
导数的物理意义2.求函数的导数的步骤:说明:上面的方法中把x换x0即为求函数在点x0处的 导数.
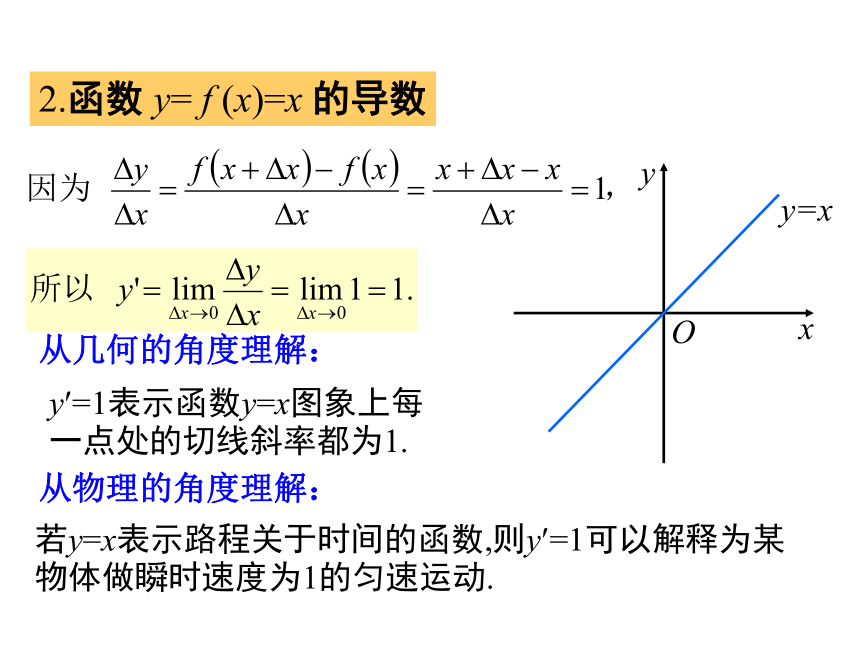
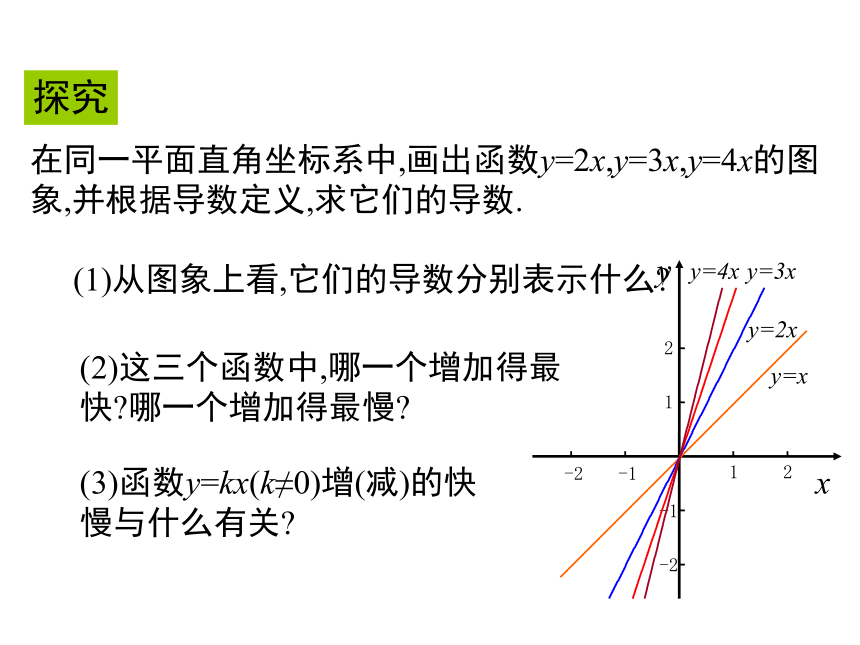
二、几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.1. 函数y=f(x)=c (c为常数)1.函数 y = f (x) =c 的导数y?=0表示函数y=x图象上每一点处的切线的斜率都为0.若y=c表示路程关于时间的函数,则y?=0则为某物体的瞬时速度始终为0,即一直处于静止状态.从几何的角度理解:从物理的角度理解:2.函数 y= f (x)=x 的导数y?=1表示函数y=x图象上每一点处的切线斜率都为1.若y=x表示路程关于时间的函数,则y?=1可以解释为某物体做瞬时速度为1的匀速运动.从几何的角度理解:从物理的角度理解:探究在同一平面直角坐标系中,画出函数y=2x,y=3x,y=4x的图象,并根据导数定义,求它们的导数.(1)从图象上看,它们的导数分别表示什么?(2)这三个函数中,哪一个增加得最快?哪一个增加得最慢?(3)函数y=kx(k≠0)增(减)的快慢与什么有关?函数 y= f (x)= kx 的导数3.函数 y = f (x) = x2 的导数 y? =2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,说明随着x的变化,切线的斜率也在变化.从导数作为函数在一点的瞬时变化率来看,y?=2x表明: 当x<0时,随着x的增加,y=x2减少得越来越慢; 当x>0时,随着x的增加,y=x2增加得越来越快.
若y=x2表示路程关于时间的函数,则y?=2x可以解释为某物体作变速运动,它在时刻x的瞬时速度为2x.从几何的角度理解:从物理的角度理解:4.函数 y = f (x) = 的导数探究画出函数 的图象.根据图象,描述它的变化情况,并求出曲线在点(1,1)处的切线方程.5.函数 y = f (x) = 的导数归纳1.若 f (x)=c(c为常数), 则f ?(x)=0 ;
2.若 f (x)=x, 则f ?(x)=1 ;
3.若 f (x)=x2 ,则f ?(x)=2x ;推广:三、知识应用,深化理解2)课堂练习五、归纳小结、布置作业(1)这节课你学到了什么?
(2)几个常见函数的导数?
导数的物理意义2.求函数的导数的步骤:说明:上面的方法中把x换x0即为求函数在点x0处的 导数.
二、几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.1. 函数y=f(x)=c (c为常数)1.函数 y = f (x) =c 的导数y?=0表示函数y=x图象上每一点处的切线的斜率都为0.若y=c表示路程关于时间的函数,则y?=0则为某物体的瞬时速度始终为0,即一直处于静止状态.从几何的角度理解:从物理的角度理解:2.函数 y= f (x)=x 的导数y?=1表示函数y=x图象上每一点处的切线斜率都为1.若y=x表示路程关于时间的函数,则y?=1可以解释为某物体做瞬时速度为1的匀速运动.从几何的角度理解:从物理的角度理解:探究在同一平面直角坐标系中,画出函数y=2x,y=3x,y=4x的图象,并根据导数定义,求它们的导数.(1)从图象上看,它们的导数分别表示什么?(2)这三个函数中,哪一个增加得最快?哪一个增加得最慢?(3)函数y=kx(k≠0)增(减)的快慢与什么有关?函数 y= f (x)= kx 的导数3.函数 y = f (x) = x2 的导数 y? =2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,说明随着x的变化,切线的斜率也在变化.从导数作为函数在一点的瞬时变化率来看,y?=2x表明: 当x<0时,随着x的增加,y=x2减少得越来越慢; 当x>0时,随着x的增加,y=x2增加得越来越快.
若y=x2表示路程关于时间的函数,则y?=2x可以解释为某物体作变速运动,它在时刻x的瞬时速度为2x.从几何的角度理解:从物理的角度理解:4.函数 y = f (x) = 的导数探究画出函数 的图象.根据图象,描述它的变化情况,并求出曲线在点(1,1)处的切线方程.5.函数 y = f (x) = 的导数归纳1.若 f (x)=c(c为常数), 则f ?(x)=0 ;
2.若 f (x)=x, 则f ?(x)=1 ;
3.若 f (x)=x2 ,则f ?(x)=2x ;推广:三、知识应用,深化理解2)课堂练习五、归纳小结、布置作业(1)这节课你学到了什么?
(2)几个常见函数的导数?
