1.2.2 基本初等函数的导数公式及导数的运算法则(一)课件19张PPT
文档属性
| 名称 | 1.2.2 基本初等函数的导数公式及导数的运算法则(一)课件19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 454.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 00:00:00 | ||
图片预览






文档简介
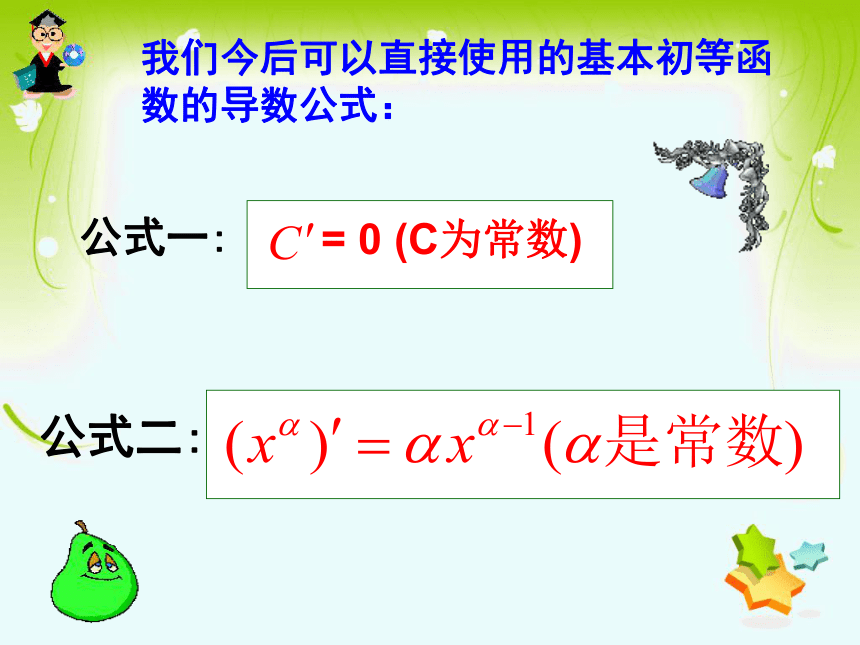
课件19张PPT。1.2.2 基本初等函数的导数公式及导数的运算法则(一)公式二:公式一:我们今后可以直接使用的基本初等函数的导数公式:算一算:求下列函数的导数(1) y=x4 ;(2) y=x-5 ;注意公式中,n的任意性.4x3-5x-6-2x-3公式三:公式四:公式五:指数函数的导数注意: 是两个不同的函数,例如:公式六:对数函数的导数1.对基本初等函数的导数公式的理解:
(1)基本初等函数的求导公式只要求记住公式的形式,学会使用公式解题即可,对公式的推导不要求掌握.
(2)要注意幂函数与指数函数的求导公式的区别,这是易错点.
练一练:(1)下列各式正确的是( )C(2)下列各式正确的是( )D3.曲线y=xn在x=2处的导数为12,则n等于( )
A.1 B.2
C.3 D.4
解析:y′|x=2=n·2n-1=12,解得n=3.
答案:C法则1:[f(x) ±g(x)] ′= f'(x) ± g'(x);应用1: 求下列函数的导数(1)y=x3+sinx
(2)y=x4-x2-x+3.即两个函数的和(或差)的导数,等于这两个函数的导数的和(或差).和差导数可推广到任意有限个 应用2:求下列函数的导数
(1)y=(2x2+3)(3x-2)(2)y=(1+x6)(2+sinx)法则2:即两个函数积的导数,等于第一个函数的导数乘上第二个函数,加上第一个函数乘上第二个函数的导数. 推论: [cf(x)]′=cf′(x)法则3:应用3:求下列函数的导数(1)y=tanx注意:商的导数分子中间是“-”,先子导再母导。 1.多项式的积的导数,通常先展开再求导更简便.
2.含根号的函数求导一般先化为分数指数幂,再求导.
练习1:求下列函数的导数(1)
(2)
(3)
(4)
7、(2)已知 若 则a=( ) A B C D D(3) 若 则a=( )
A 6 B 3 C 0 D -2
B课堂小结 1. 由常函数、幂函数及正、余弦函数经加、减、乘运算得到的简单的函数均可利用求导法则与导数公式求导,而不需要回到导数的定义去求此类简单函数的导数 .2.导数的运算法则1. [f(x) ±g(x)] ′=f′(x) ±g(x) ′2. [f(x) .g(x)] ′=f′(x) g(x)± f(x) g(x) ′
(1)基本初等函数的求导公式只要求记住公式的形式,学会使用公式解题即可,对公式的推导不要求掌握.
(2)要注意幂函数与指数函数的求导公式的区别,这是易错点.
练一练:(1)下列各式正确的是( )C(2)下列各式正确的是( )D3.曲线y=xn在x=2处的导数为12,则n等于( )
A.1 B.2
C.3 D.4
解析:y′|x=2=n·2n-1=12,解得n=3.
答案:C法则1:[f(x) ±g(x)] ′= f'(x) ± g'(x);应用1: 求下列函数的导数(1)y=x3+sinx
(2)y=x4-x2-x+3.即两个函数的和(或差)的导数,等于这两个函数的导数的和(或差).和差导数可推广到任意有限个 应用2:求下列函数的导数
(1)y=(2x2+3)(3x-2)(2)y=(1+x6)(2+sinx)法则2:即两个函数积的导数,等于第一个函数的导数乘上第二个函数,加上第一个函数乘上第二个函数的导数. 推论: [cf(x)]′=cf′(x)法则3:应用3:求下列函数的导数(1)y=tanx注意:商的导数分子中间是“-”,先子导再母导。 1.多项式的积的导数,通常先展开再求导更简便.
2.含根号的函数求导一般先化为分数指数幂,再求导.
练习1:求下列函数的导数(1)
(2)
(3)
(4)
7、(2)已知 若 则a=( ) A B C D D(3) 若 则a=( )
A 6 B 3 C 0 D -2
B课堂小结 1. 由常函数、幂函数及正、余弦函数经加、减、乘运算得到的简单的函数均可利用求导法则与导数公式求导,而不需要回到导数的定义去求此类简单函数的导数 .2.导数的运算法则1. [f(x) ±g(x)] ′=f′(x) ±g(x) ′2. [f(x) .g(x)] ′=f′(x) g(x)± f(x) g(x) ′
