1.2.2 基本初等函数的导数公式及导数的运算法则课件24张PPT
文档属性
| 名称 | 1.2.2 基本初等函数的导数公式及导数的运算法则课件24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 239.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:06:51 | ||
图片预览




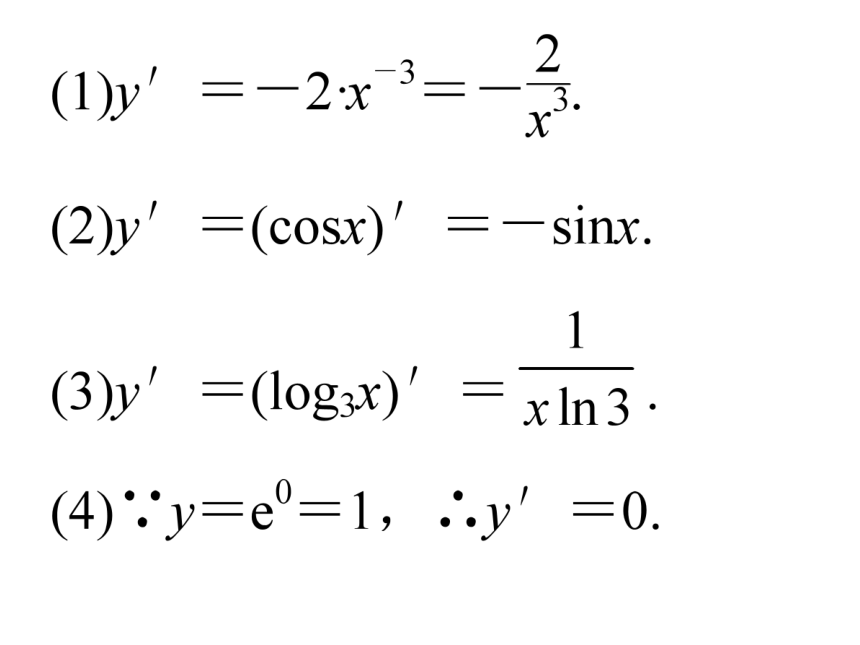



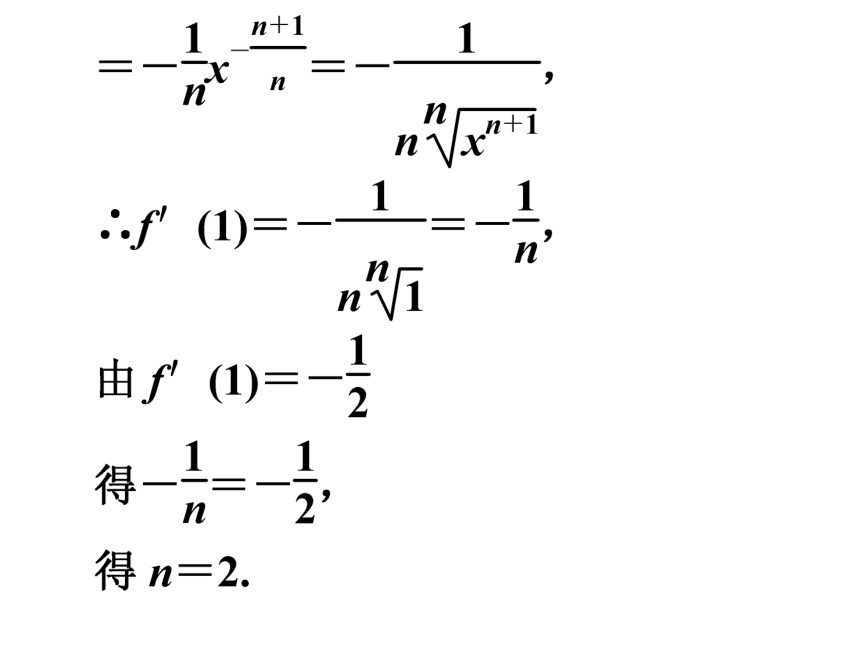
文档简介
课件24张PPT。1.2.2 基本初等函数的导数公式及导数的运算法则高二数学选修2-2 人教版2003五种常见函数的导数公式及应用复习引入:我们今后可以直接使用的基本初等函数的导数公式求下列函数的导数:
(1)y=x-2 (2)y=cosx
(3)y=log3x (4)y=e0
随堂练习1:随堂练习2:【思维总结】 求函数在某一点处的导数需要先对原函数进行求导,再将变量值代入导函数求解。例1 假设某国家在20年期间的平均通货膨胀率为5%,物价p(单位:元)与时间t(单位:年)有如下函数关系
其中p0为t = 0时的物价。假定某种商品的p0=1,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01)?解:根据基本初等函数导数公式表,有因此,在第10个年头,这种商品的价格约以0.08元/年的速度上涨。导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:例2 根据基本初等函数的导数公式和导数运算法则,求函数y=x3-2x+3的导数。解:因为y′=(x3-2x+3) ′= (x3) ′-(2x) ′+(3) ′=3x2-2∴函数y=x3-2x+3的导数是y′=3x2-2随堂练习3:随堂练习3:例3 日常生活中的饮用水通常是经过净化的。随着水纯净度的提高,所需净化费用不断增加。已知将1吨水净化到纯净度x%时所需费用(单位:元)为求净化到下列纯净度时,所需净化费用的瞬时变化率: (1)90% (2)98%解:净化费用的瞬时变化率就是净化费用函数的导数所以,纯净度为90%时,费用的瞬时变化率是52.84元/吨所以,纯净度为98%时,费用的瞬时变化率是1321元/吨小结:1、基本初等函数的导数公式及应用
2、导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:作业作业(选做)
(1)y=x-2 (2)y=cosx
(3)y=log3x (4)y=e0
随堂练习1:随堂练习2:【思维总结】 求函数在某一点处的导数需要先对原函数进行求导,再将变量值代入导函数求解。例1 假设某国家在20年期间的平均通货膨胀率为5%,物价p(单位:元)与时间t(单位:年)有如下函数关系
其中p0为t = 0时的物价。假定某种商品的p0=1,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01)?解:根据基本初等函数导数公式表,有因此,在第10个年头,这种商品的价格约以0.08元/年的速度上涨。导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:例2 根据基本初等函数的导数公式和导数运算法则,求函数y=x3-2x+3的导数。解:因为y′=(x3-2x+3) ′= (x3) ′-(2x) ′+(3) ′=3x2-2∴函数y=x3-2x+3的导数是y′=3x2-2随堂练习3:随堂练习3:例3 日常生活中的饮用水通常是经过净化的。随着水纯净度的提高,所需净化费用不断增加。已知将1吨水净化到纯净度x%时所需费用(单位:元)为求净化到下列纯净度时,所需净化费用的瞬时变化率: (1)90% (2)98%解:净化费用的瞬时变化率就是净化费用函数的导数所以,纯净度为90%时,费用的瞬时变化率是52.84元/吨所以,纯净度为98%时,费用的瞬时变化率是1321元/吨小结:1、基本初等函数的导数公式及应用
2、导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:作业作业(选做)
