2.1.2 演绎推理课件16张PPT
文档属性
| 名称 | 2.1.2 演绎推理课件16张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 815.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:07:19 | ||
图片预览





文档简介
课件16张PPT。复习:合情推理归纳推理 从特殊到一般
类比推理 从特殊到特殊从具体问题出发观察、分析
比较、联想提出猜想归纳
类比 观察、思考是合情推理吗?从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.注:1.演绎推理是从一般到特殊的推理;2.“三段论”是演绎推理的一般模式,包括
⑴大前提---已知的一般原理;
⑵小前提---所研究的特殊情况;
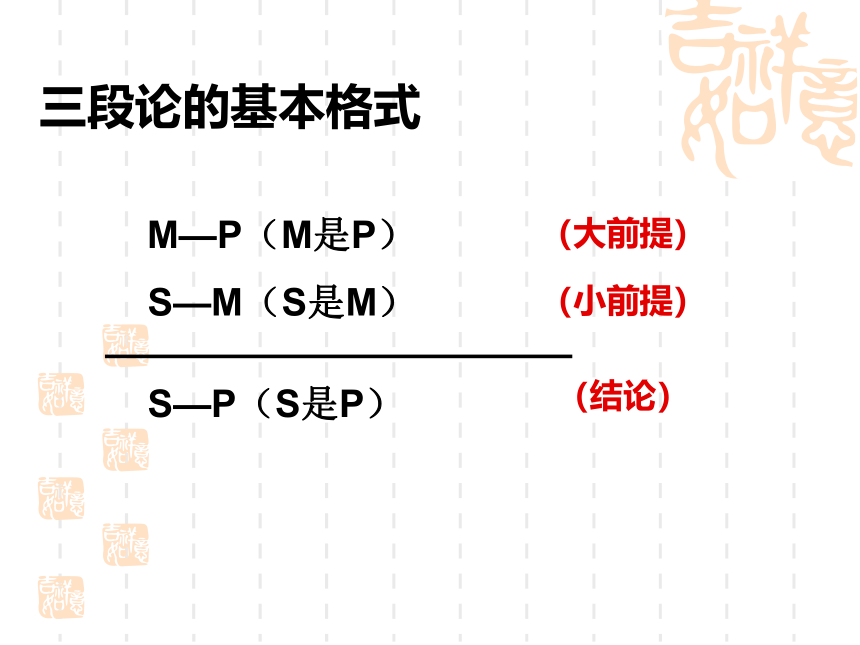
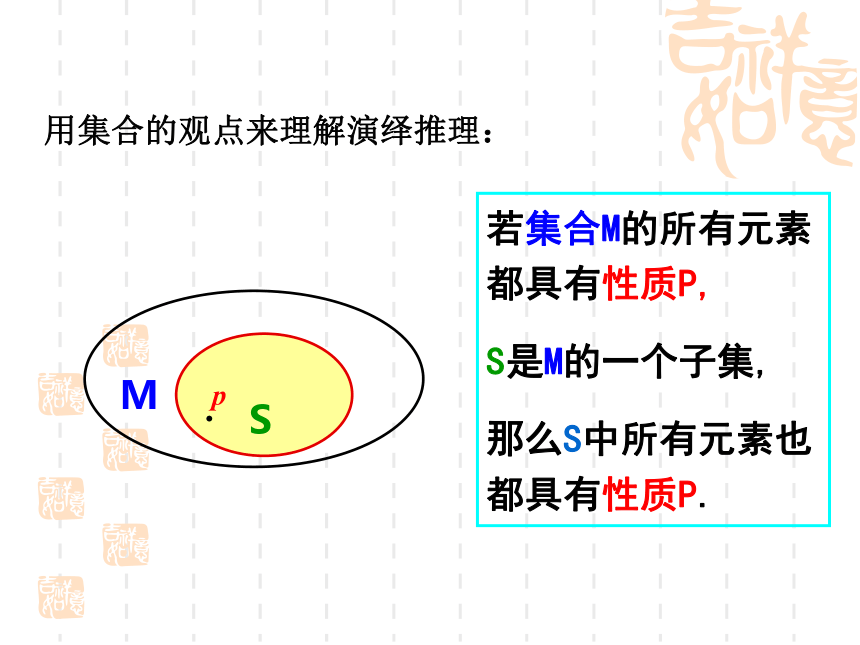
⑶结论- - - 据一般原理,对特殊情况做出的判断. 演绎推理三段论的基本格式M—P(M是P)S—M(S是M)S—P(S是P)(大前提)(小前提)(结论)用集合的观点来理解演绎推理:SM若集合M的所有元素都具有性质P,
S是M的一个子集,
那么S中所有元素也都具有性质P. 观察与思考1.所有的金属都能导电, 2.一切奇数都不能被2整除, 所以,铜能够导电.铜是金属, 所以,(2100+1)不能被2整除.(2100+1)是奇数, 演绎推理解:二次函数的图象是一条抛物线 (大前提)练习1:判断下列推理是否正确,并分析原因:(1)整数是自然数,-3是整数,-3是自然数;(2)无理数是无限小数,是无限小数,是无理数.在演绎推理中,只要前提和推理形式是正确的,则结论必定是正确的。练习2:将下列推理写成“三段论”的形式:(1)向量是既有大小又有方向的量,故零向量也有大小和方向;
(2) 是有理数;
(3)y=sinx是周期函数。例2:如图,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E是垂足,求证AB的中点M到D,E的距离相等。证明:∵有一个内角是直角的三角形是直角三角形,在△ABC中,AD⊥BC,即∠ADB=90o∴△ABD是直角三角形.同理△ABE是直角三角形∵直角三角形斜边上的中线等于斜边的一半,M是Rt△ABD斜边AB的中点,DM是斜边上的中线.∴DM= AB/2 .同理 EM= AB/2.∴DM = EM.大前提小前提结论大前提小前提结论例2:如图,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E是垂足,求证AB的中点M到D,E的距离相等。证明:∵在△ABC中,AD⊥BC,即∠ADB=90o∴△ABD是直角三角形.同理△ABE是直角三角形∵M是Rt△ABD斜边AB的中点,DM是斜边上的中线.∴DM= AB/2.同理 EM= AB/2.∴DM = EM.作为一般性原理的大前提被人们熟知,是显然的,所以书写时可以省略不写。例3:证明函数 在 内是增函数合情推理与演绎推理的区别:1 从推理的形式来看:
①归纳是由特殊到一般的推理;
②类比是由特殊到特殊的推理;
③演绎推理是由一般到特殊的
推理.
2 从推理的结论来看:
合情推理的结论不一定正确,有待证明;
演绎推理得到的结论一定正确.2 数学结论、证明思路的发现,主要靠合情推理.1 演绎推理是证明数学结论、建立数学体系的重要思维过程.合情推理与演绎推理的相关说明:谢谢!作业:课时跟踪检测(演绎推理)
类比推理 从特殊到特殊从具体问题出发观察、分析
比较、联想提出猜想归纳
类比 观察、思考是合情推理吗?从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.注:1.演绎推理是从一般到特殊的推理;2.“三段论”是演绎推理的一般模式,包括
⑴大前提---已知的一般原理;
⑵小前提---所研究的特殊情况;
⑶结论- - - 据一般原理,对特殊情况做出的判断. 演绎推理三段论的基本格式M—P(M是P)S—M(S是M)S—P(S是P)(大前提)(小前提)(结论)用集合的观点来理解演绎推理:SM若集合M的所有元素都具有性质P,
S是M的一个子集,
那么S中所有元素也都具有性质P. 观察与思考1.所有的金属都能导电, 2.一切奇数都不能被2整除, 所以,铜能够导电.铜是金属, 所以,(2100+1)不能被2整除.(2100+1)是奇数, 演绎推理解:二次函数的图象是一条抛物线 (大前提)练习1:判断下列推理是否正确,并分析原因:(1)整数是自然数,-3是整数,-3是自然数;(2)无理数是无限小数,是无限小数,是无理数.在演绎推理中,只要前提和推理形式是正确的,则结论必定是正确的。练习2:将下列推理写成“三段论”的形式:(1)向量是既有大小又有方向的量,故零向量也有大小和方向;
(2) 是有理数;
(3)y=sinx是周期函数。例2:如图,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E是垂足,求证AB的中点M到D,E的距离相等。证明:∵有一个内角是直角的三角形是直角三角形,在△ABC中,AD⊥BC,即∠ADB=90o∴△ABD是直角三角形.同理△ABE是直角三角形∵直角三角形斜边上的中线等于斜边的一半,M是Rt△ABD斜边AB的中点,DM是斜边上的中线.∴DM= AB/2 .同理 EM= AB/2.∴DM = EM.大前提小前提结论大前提小前提结论例2:如图,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D,E是垂足,求证AB的中点M到D,E的距离相等。证明:∵在△ABC中,AD⊥BC,即∠ADB=90o∴△ABD是直角三角形.同理△ABE是直角三角形∵M是Rt△ABD斜边AB的中点,DM是斜边上的中线.∴DM= AB/2.同理 EM= AB/2.∴DM = EM.作为一般性原理的大前提被人们熟知,是显然的,所以书写时可以省略不写。例3:证明函数 在 内是增函数合情推理与演绎推理的区别:1 从推理的形式来看:
①归纳是由特殊到一般的推理;
②类比是由特殊到特殊的推理;
③演绎推理是由一般到特殊的
推理.
2 从推理的结论来看:
合情推理的结论不一定正确,有待证明;
演绎推理得到的结论一定正确.2 数学结论、证明思路的发现,主要靠合情推理.1 演绎推理是证明数学结论、建立数学体系的重要思维过程.合情推理与演绎推理的相关说明:谢谢!作业:课时跟踪检测(演绎推理)
