3.1.2 复数的几何意义课件24张PPT
文档属性
| 名称 | 3.1.2 复数的几何意义课件24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:09:55 | ||
图片预览




文档简介
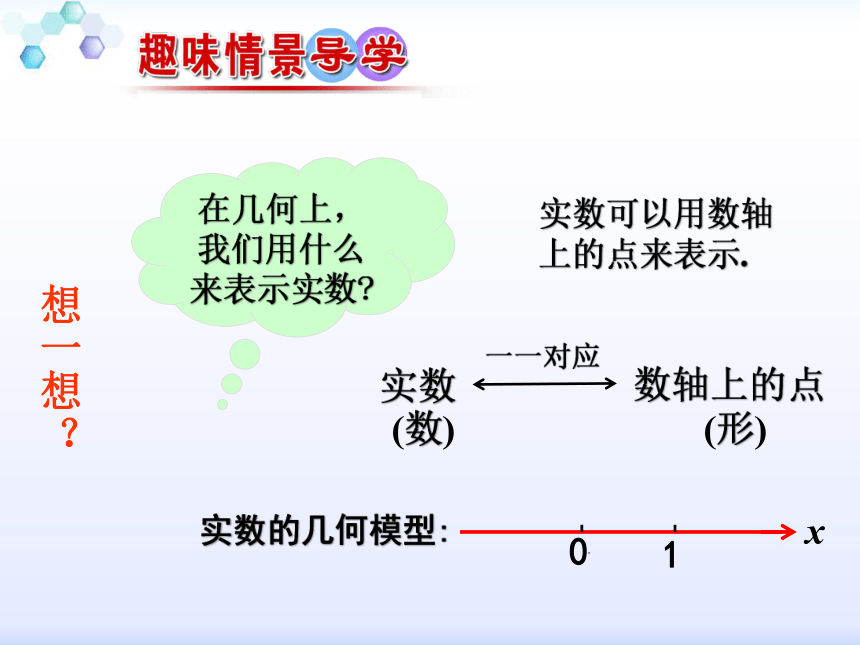
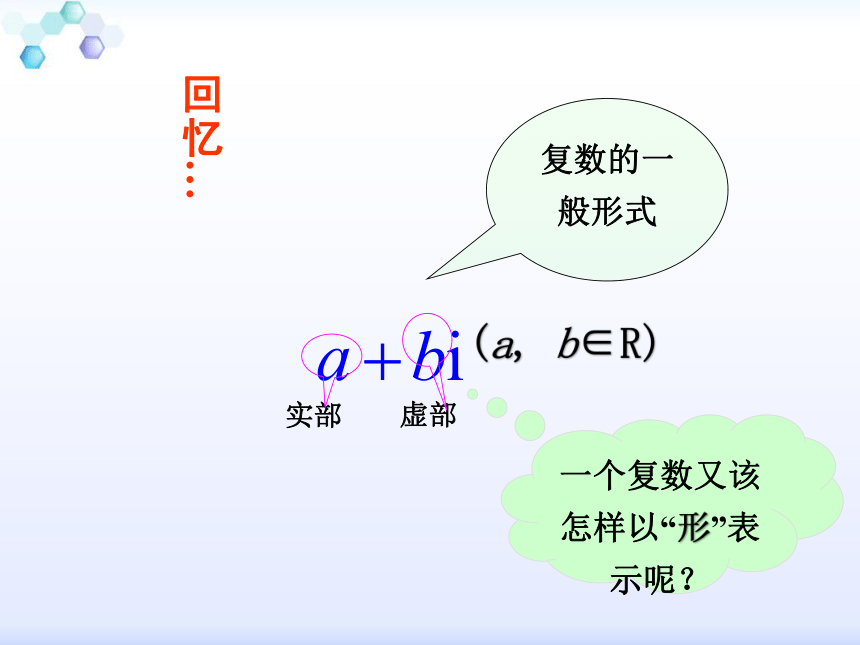
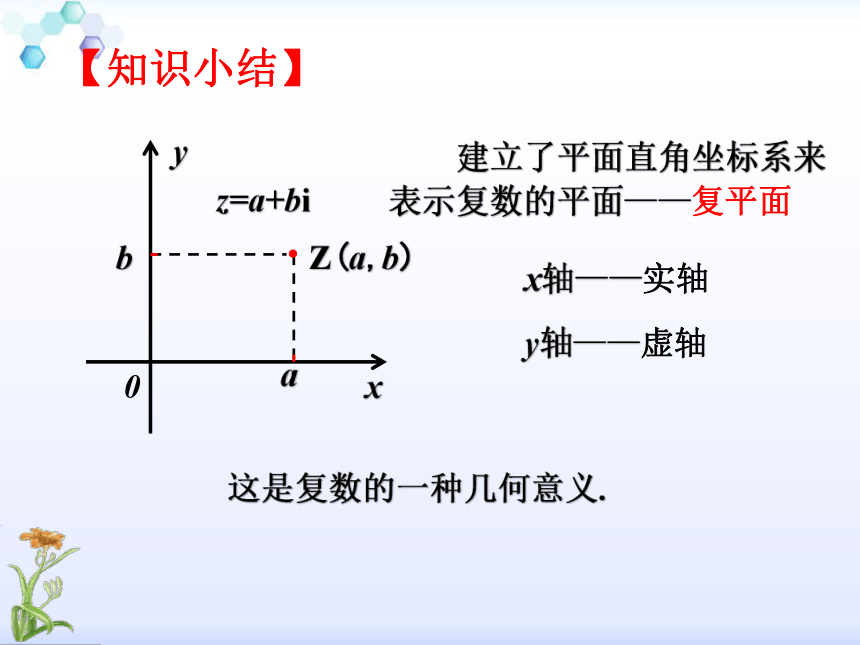
课件24张PPT。3.1.2 复数的几何意义 在几何上,我们用什么来表示实数?实数可以用数轴上的点来表示.实数 数轴上的点 (形)(数)一一对应 想一想?复数的一般形式一个复数又该怎样以“形”表示呢?回忆…实部虚部(a, b∈R)有序实数对(a,b)一一对应一一对应一一对应探究点1 复数的几何表示实部虚部Z(a,b) 建立了平面直角坐标系来表示复数的平面——复平面x轴——实轴y轴——虚轴z=a+bi这是复数的一种几何意义.【知识小结】例1 ①Z=-2+3i表示的点为例2 ①点(-6,5)表示的复数为
②点(0,-3)表示的复数为(-2,3)② Z=-7i表示的点为(0,-7)Z=-6+5iZ=-3i
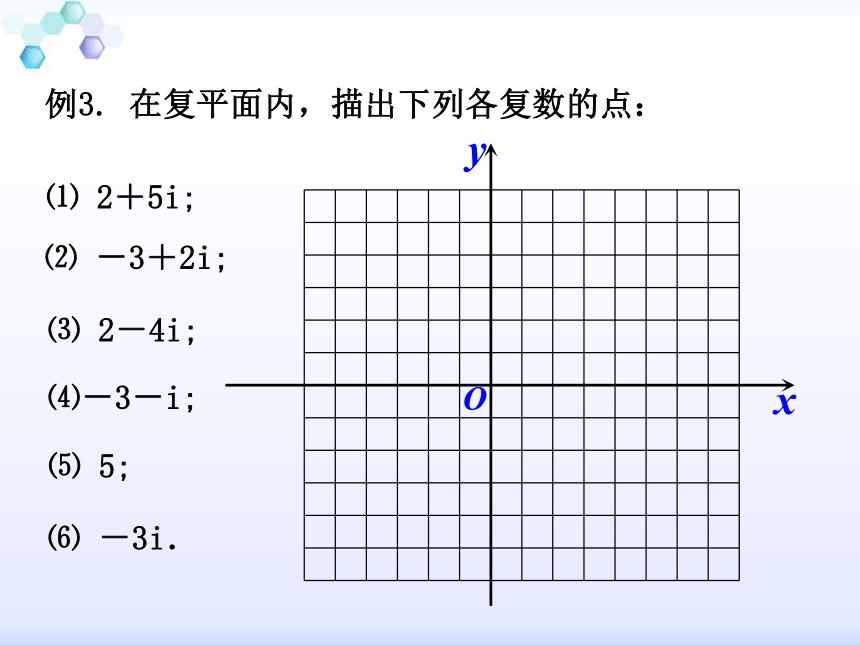
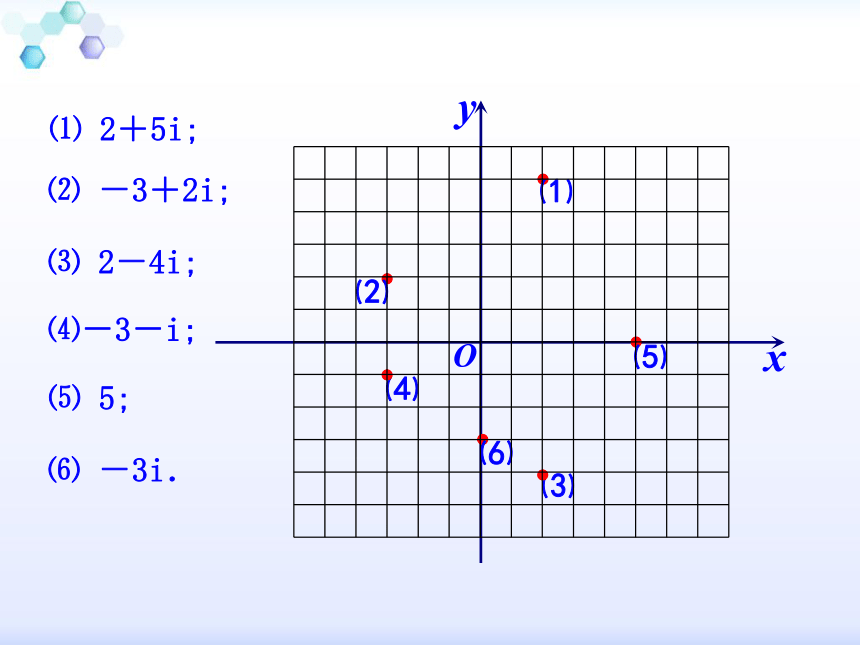
例3. 在复平面内,描出下列各复数的点:xyO⑴ 2+5i;⑵ -3+2i;⑶ 2-4i;⑷-3-i;⑸ 5;⑹ -3i.xyO⑵⑷⑶⑸⑴⑹⑴ 2+5i;⑵ -3+2i;⑶ 2-4i;⑷-3-i;⑸ 5;⑹ -3i.例4. 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围. (A)在复平面内,对应于实数的点都在实轴上;
(B)在复平面内,对应于纯虚数的点都在虚轴上;
(C)在复平面内,实轴上的点所对应的复数都是实数;
(D)在复平面内,虚轴上的点所对应的复数都是纯虚数.下列命题中的假命题是( )D【即时训练】 实轴上的点表示实数,虚轴上的点除原点外都表示纯虚数,各象限内的点表示实部不为零的虚数.【总结提升】
一般地,实轴上的点,虚轴上的点,各象限内的点分别表示什么样的数?【变式训练1】:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。 解:因为复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2) 所以(m2+m-6)-2(m2+m-2)+4=0 所以m=1或m=-2复数z=a+bi有序实数对(a,b)一一对应一一对应一一对应探究点2 复数的向量表示一一对应这是复数的又一种几何意义.?复数的模其实是实数绝对值概念的推广xOz=a+biy|z|=r=|OZ|探究点3 复数的模的几何意义: 复数 z=a+bi的模r就是复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.Z(a,b)?提问:复数Z1,Z2能比较大小吗?若复数z(x,y)对应点集为圆: 试求│z│的最大值与最小值.o1211【变式训练2】:31?想一想:
利用复数几何意义
如何表示该圆?|z+1+ i|=1【课堂讨论】复数z满足|z-(1+i)|-|z-(-1+i)|=2,则复平面内z对应的点
的轨迹是什么?射线(-1,1)(1,1)Oyx 解决复数在复平面内对应的几何图形问题,要熟练掌握两点:
①复数z=x+yi(x,y∈R)在复平面上的对应点Z(x,y);
②|z|的几何意义为Z在复平面上对应的点Z(x,y)与原点的距离。
③明确|z-(a+bi)|的几何意义是复数z对应的点与点(a,b)之间的距离。【总结提升】1.“a=0”是“复数a+bi (a , b∈R)所对应的点
在虚轴上”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分不必要条件C课堂达标演练2.已知复数z满足|Z|2-2|Z|-3=0,则复数Z对应的轨迹是( )
A 1个圆 B 线段 C 2个点 D 2个圆A3.已知复数 解析:因为|Z|=a(a>0)表示以原点为圆心,a为半径的圆
又 |Z1|=2 |Z2|=1
故|Z2|≤|Z|≤|Z1|,1 ≤|Z|≤2即对应的点Z的集合
是以原点为圆心,以1和2为半径的圆环,
如图所示:120xy则满足条件|Z2|≤|Z|≤|Z1|E的点Z的集合是什么图形?一种认识:
点、平面向量与复数的一一对应关系;
两种意义:
复数对应的点,复数的模;
三种思想:
数形结合的思想,
转化与化归的思想,
方程与不等式思想。 The End
②点(0,-3)表示的复数为(-2,3)② Z=-7i表示的点为(0,-7)Z=-6+5iZ=-3i
例3. 在复平面内,描出下列各复数的点:xyO⑴ 2+5i;⑵ -3+2i;⑶ 2-4i;⑷-3-i;⑸ 5;⑹ -3i.xyO⑵⑷⑶⑸⑴⑹⑴ 2+5i;⑵ -3+2i;⑶ 2-4i;⑷-3-i;⑸ 5;⑹ -3i.例4. 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围. (A)在复平面内,对应于实数的点都在实轴上;
(B)在复平面内,对应于纯虚数的点都在虚轴上;
(C)在复平面内,实轴上的点所对应的复数都是实数;
(D)在复平面内,虚轴上的点所对应的复数都是纯虚数.下列命题中的假命题是( )D【即时训练】 实轴上的点表示实数,虚轴上的点除原点外都表示纯虚数,各象限内的点表示实部不为零的虚数.【总结提升】
一般地,实轴上的点,虚轴上的点,各象限内的点分别表示什么样的数?【变式训练1】:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。 解:因为复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2) 所以(m2+m-6)-2(m2+m-2)+4=0 所以m=1或m=-2复数z=a+bi有序实数对(a,b)一一对应一一对应一一对应探究点2 复数的向量表示一一对应这是复数的又一种几何意义.?复数的模其实是实数绝对值概念的推广xOz=a+biy|z|=r=|OZ|探究点3 复数的模的几何意义: 复数 z=a+bi的模r就是复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.Z(a,b)?提问:复数Z1,Z2能比较大小吗?若复数z(x,y)对应点集为圆: 试求│z│的最大值与最小值.o1211【变式训练2】:31?想一想:
利用复数几何意义
如何表示该圆?|z+1+ i|=1【课堂讨论】复数z满足|z-(1+i)|-|z-(-1+i)|=2,则复平面内z对应的点
的轨迹是什么?射线(-1,1)(1,1)Oyx 解决复数在复平面内对应的几何图形问题,要熟练掌握两点:
①复数z=x+yi(x,y∈R)在复平面上的对应点Z(x,y);
②|z|的几何意义为Z在复平面上对应的点Z(x,y)与原点的距离。
③明确|z-(a+bi)|的几何意义是复数z对应的点与点(a,b)之间的距离。【总结提升】1.“a=0”是“复数a+bi (a , b∈R)所对应的点
在虚轴上”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分不必要条件C课堂达标演练2.已知复数z满足|Z|2-2|Z|-3=0,则复数Z对应的轨迹是( )
A 1个圆 B 线段 C 2个点 D 2个圆A3.已知复数 解析:因为|Z|=a(a>0)表示以原点为圆心,a为半径的圆
又 |Z1|=2 |Z2|=1
故|Z2|≤|Z|≤|Z1|,1 ≤|Z|≤2即对应的点Z的集合
是以原点为圆心,以1和2为半径的圆环,
如图所示:120xy则满足条件|Z2|≤|Z|≤|Z1|E的点Z的集合是什么图形?一种认识:
点、平面向量与复数的一一对应关系;
两种意义:
复数对应的点,复数的模;
三种思想:
数形结合的思想,
转化与化归的思想,
方程与不等式思想。 The End
