复数的几何意义课件19张PPT
文档属性
| 名称 | 复数的几何意义课件19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 368.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:10:19 | ||
图片预览




文档简介
课件19张PPT。复数的几何意义人教A版 选修2-2自强不息 厚德载物1、复数的概念:形如______________的数叫做复数。
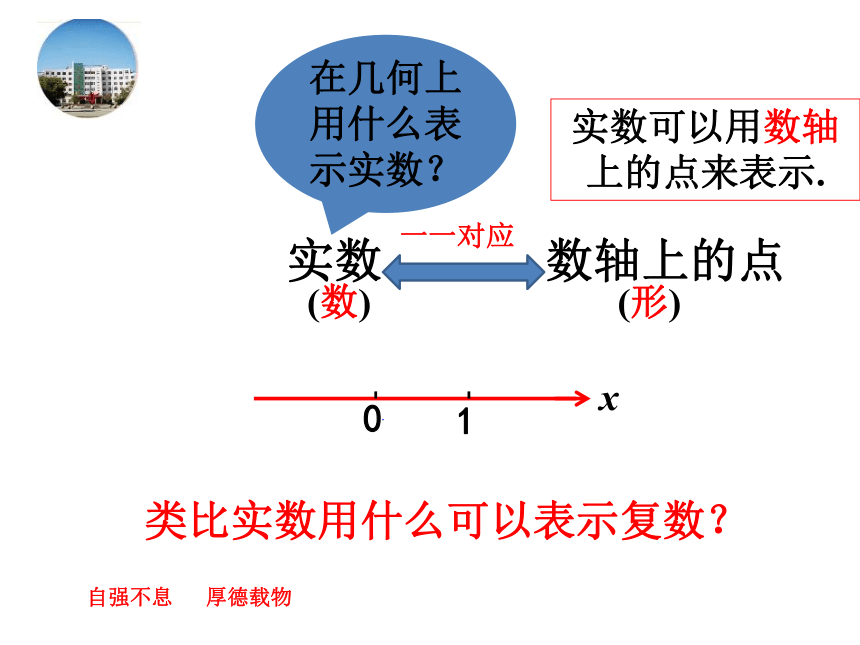
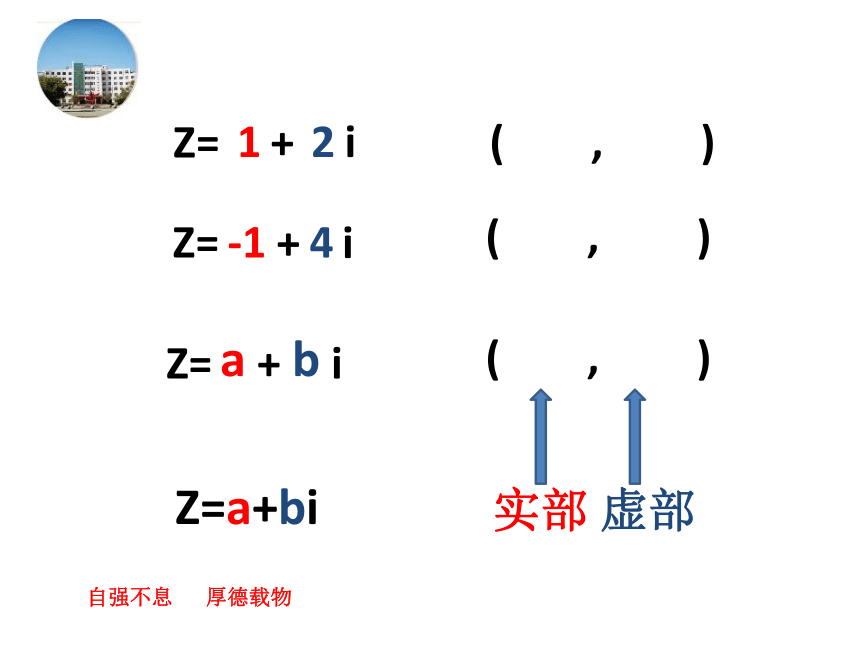
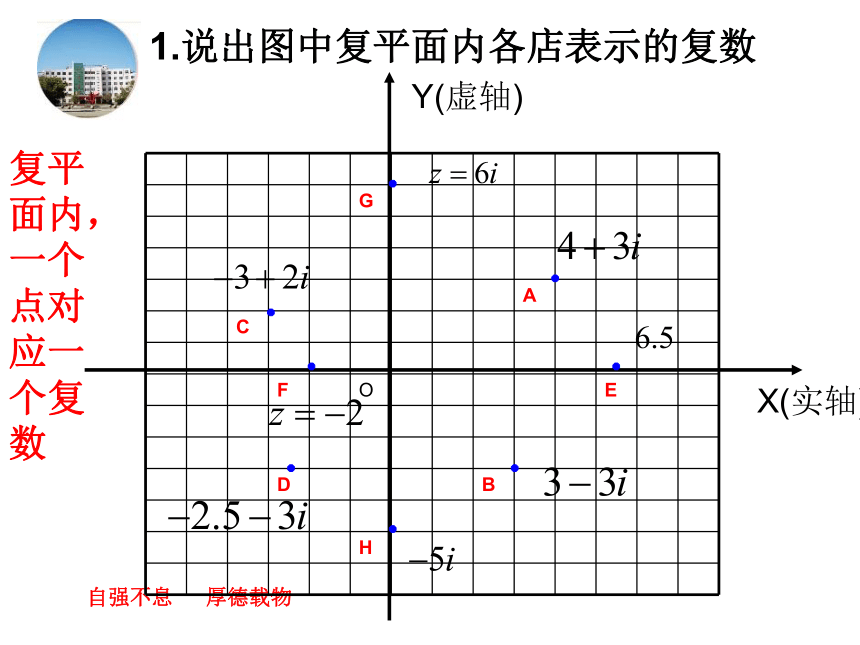
2、两个复数相等的充要条件a+bi (a,b∈R)a=0,b≠0b=0a ≠ 0,b≠0自强不息 厚德载物纯虚数实数非纯虚数复习引入虚部实部实数可以用数轴上的点来表示.实数 数轴上的点 (形)(数)一一对应 类比实数用什么可以表示复数?在几何上用什么表示实数?自强不息 厚德载物1Z=+2i( , )Z=Z=-1+4ia+bi( , )( , )自强不息 厚德载物Z=a+bi实部虚部 复平面的概念:建立了平面直角坐标系来表示复数的平面叫复数平面 (简称复平面)自强不息 厚德载物讲授新课自强不息 厚德载物1.说出图中复平面内各店表示的复数X(实轴)Y(虚轴)复平面内,一个点对应一个复数4365O212.在复平面内,描出表示下列各复数的点X实轴Y虚轴(1) 2+5i ;
(2) -3+2i;
(3) 2-4i;
(4) -3-i;
(5) 5;
(6) -3i;
(7)一个复数对应一个点复平面内的点
z(a,b)复数
Z=a+bi一一对应复平面内的
点Z(a,b)平面向量一一对应自强不息 厚德载物O3.已知下列复数,在复平面内画出这些复数对应的向量X实轴Y虚轴(1) 2+i ;
(2) -2+4i;
(3)-2i;
(4) 4;
(5) 5-4i;1-11-1自强不息 厚德载物复数的几何意义自强不息 厚德载物一一对应数形结合的思想(数)(形)(数)OX实轴Y虚轴(1) 2+i ;
(2) -2+4i ;
(3)-2i ;
(4) 4 ;
(5) 5-4i ;1-11-1自强不息 厚德载物(2,1)(-2,4)(0,-2)(4,0)(5,-4)思考:复平面内,实轴和虚轴上
的点对应的复数有什么特点?在复平面内,实轴上的点所对应的复数都是实数.虚轴上的点(0除外)所对应的复数都是纯虚数结论:自强不息 厚德载物 例1 实数m取什么值时复数
在复平面内所对应的点
(1)位于第四象限 (2) 位于直线y=x上 自强不息 厚德载物例题讲解总结:运用数形结合的思想,几何问题和代数问
题互相转化进行计算复数的模的几何意义向量 的模r,叫做复数 z=a+bi的模,记作|Z|或| a+bi|。即在复平面上对应的点Z(a,b)到原点的距离.自强不息 厚德载物
例2 求下列复数的模
(1)z1=15-8i (2)z2=-3i (3)z3=3(4)z4=1+ai(a∈R) (5)z5=-4a+3ai(a<0)自强不息 厚德载物例题讲解 例2(2)满足|z|=4(z∈C)的z值有几个?思考:(1)满足|z|=4(z∈R)的z值有几个?这些复数对应的点在复平面上构成怎样的图形? 自强不息 厚德载物从数轴到平面直角坐标系,是从
一维上升到二维的一个过程课堂小结:1.复数的几何意义是什么?
2.如何求复数的模长?自强不息 厚德载物自强不息 厚德载物作业布置自强不息 厚德载物再 见 !
2、两个复数相等的充要条件a+bi (a,b∈R)a=0,b≠0b=0a ≠ 0,b≠0自强不息 厚德载物纯虚数实数非纯虚数复习引入虚部实部实数可以用数轴上的点来表示.实数 数轴上的点 (形)(数)一一对应 类比实数用什么可以表示复数?在几何上用什么表示实数?自强不息 厚德载物1Z=+2i( , )Z=Z=-1+4ia+bi( , )( , )自强不息 厚德载物Z=a+bi实部虚部 复平面的概念:建立了平面直角坐标系来表示复数的平面叫复数平面 (简称复平面)自强不息 厚德载物讲授新课自强不息 厚德载物1.说出图中复平面内各店表示的复数X(实轴)Y(虚轴)复平面内,一个点对应一个复数4365O212.在复平面内,描出表示下列各复数的点X实轴Y虚轴(1) 2+5i ;
(2) -3+2i;
(3) 2-4i;
(4) -3-i;
(5) 5;
(6) -3i;
(7)一个复数对应一个点复平面内的点
z(a,b)复数
Z=a+bi一一对应复平面内的
点Z(a,b)平面向量一一对应自强不息 厚德载物O3.已知下列复数,在复平面内画出这些复数对应的向量X实轴Y虚轴(1) 2+i ;
(2) -2+4i;
(3)-2i;
(4) 4;
(5) 5-4i;1-11-1自强不息 厚德载物复数的几何意义自强不息 厚德载物一一对应数形结合的思想(数)(形)(数)OX实轴Y虚轴(1) 2+i ;
(2) -2+4i ;
(3)-2i ;
(4) 4 ;
(5) 5-4i ;1-11-1自强不息 厚德载物(2,1)(-2,4)(0,-2)(4,0)(5,-4)思考:复平面内,实轴和虚轴上
的点对应的复数有什么特点?在复平面内,实轴上的点所对应的复数都是实数.虚轴上的点(0除外)所对应的复数都是纯虚数结论:自强不息 厚德载物 例1 实数m取什么值时复数
在复平面内所对应的点
(1)位于第四象限 (2) 位于直线y=x上 自强不息 厚德载物例题讲解总结:运用数形结合的思想,几何问题和代数问
题互相转化进行计算复数的模的几何意义向量 的模r,叫做复数 z=a+bi的模,记作|Z|或| a+bi|。即在复平面上对应的点Z(a,b)到原点的距离.自强不息 厚德载物
例2 求下列复数的模
(1)z1=15-8i (2)z2=-3i (3)z3=3(4)z4=1+ai(a∈R) (5)z5=-4a+3ai(a<0)自强不息 厚德载物例题讲解 例2(2)满足|z|=4(z∈C)的z值有几个?思考:(1)满足|z|=4(z∈R)的z值有几个?这些复数对应的点在复平面上构成怎样的图形? 自强不息 厚德载物从数轴到平面直角坐标系,是从
一维上升到二维的一个过程课堂小结:1.复数的几何意义是什么?
2.如何求复数的模长?自强不息 厚德载物自强不息 厚德载物作业布置自强不息 厚德载物再 见 !
