选修4-1第一讲 相似三角形的判定及有关性质 平行线分线段成比例定理 课件17张PPT
文档属性
| 名称 | 选修4-1第一讲 相似三角形的判定及有关性质 平行线分线段成比例定理 课件17张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 555.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:16:15 | ||
图片预览


文档简介
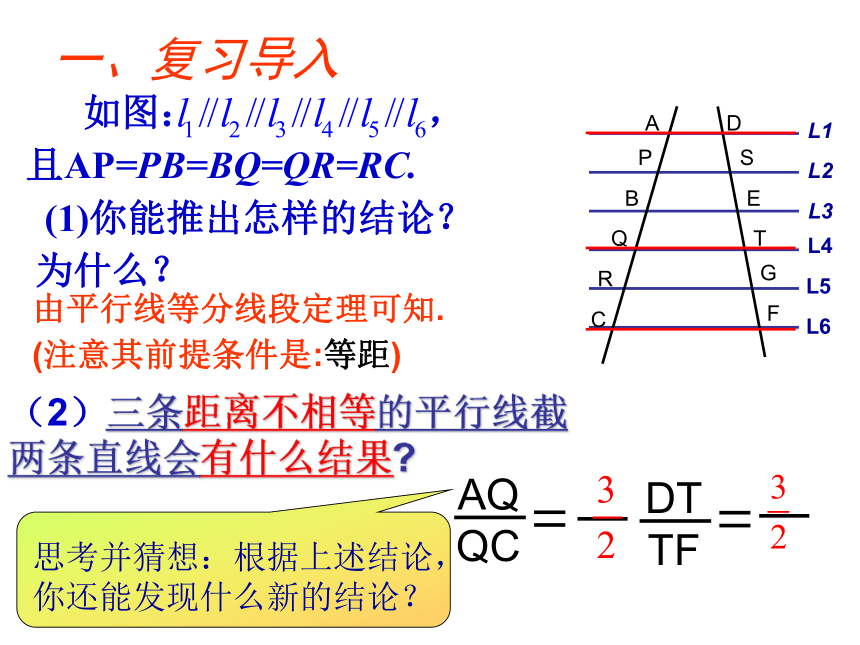
课件17张PPT。二、平行线分线段成比例定理一、复习导入AP(2)三条距离不相等的平行线截两条直线会有什么结果?由平行线等分线段定理可知.
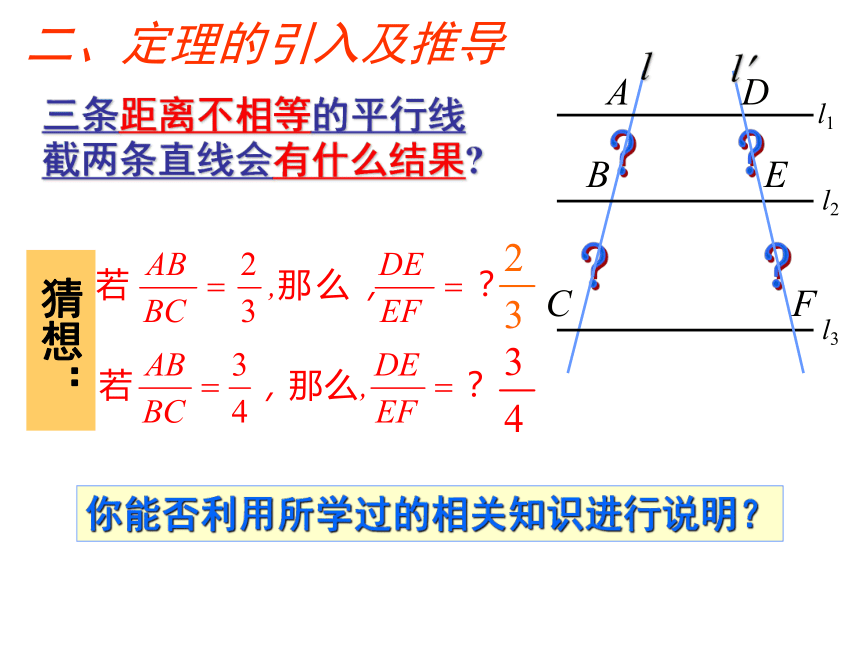
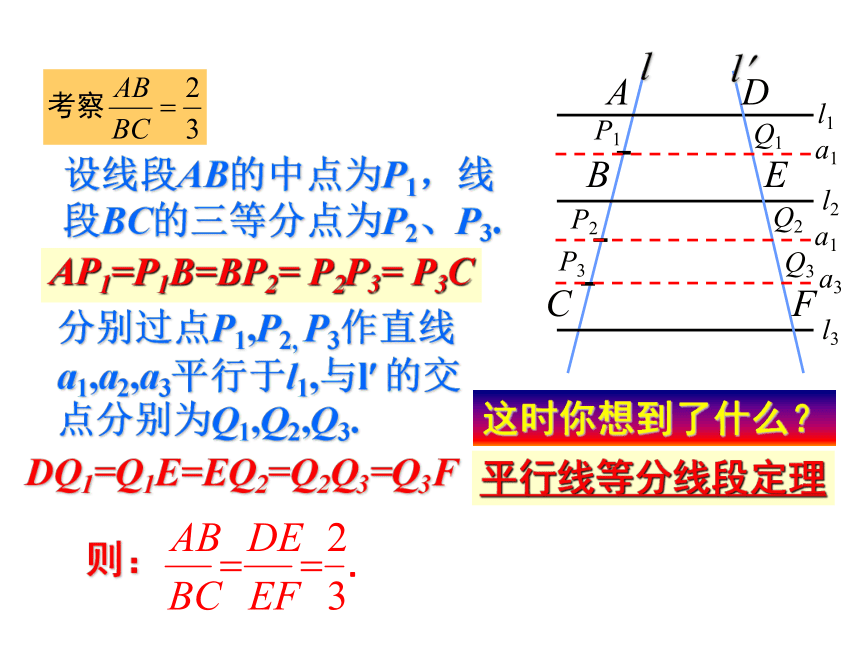
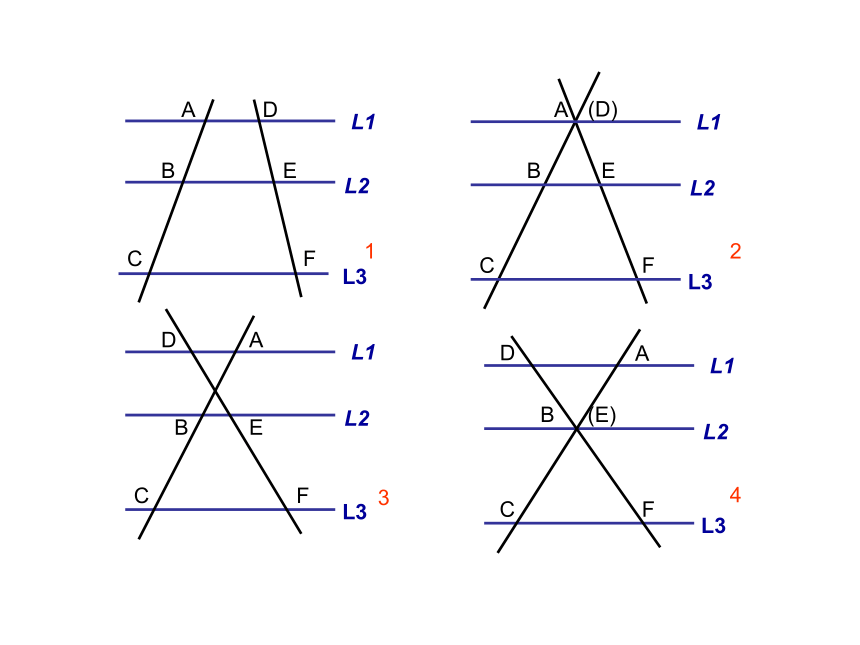
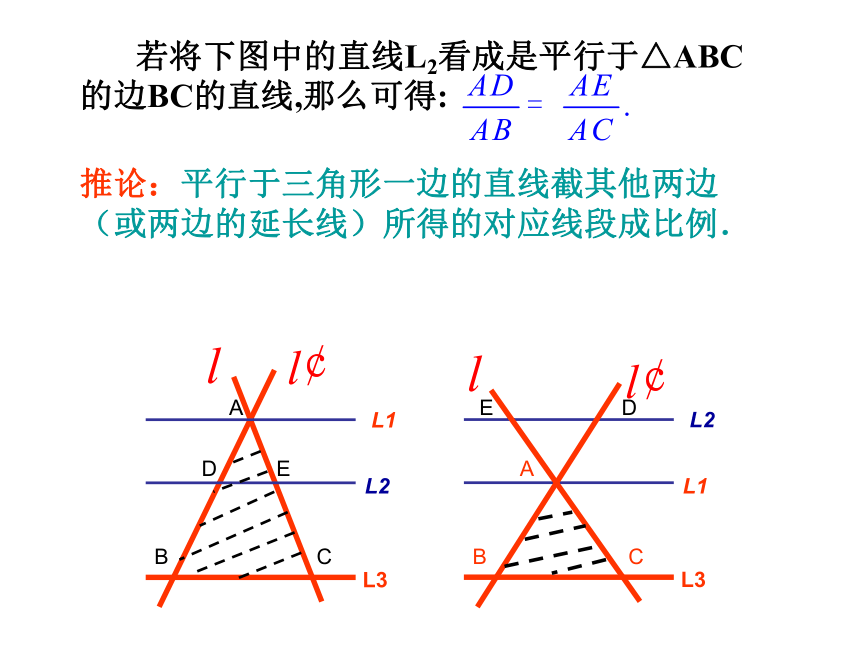
(注意其前提条件是:等距)三条距离不相等的平行线截两条直线会有什么结果?猜想:你能否利用所学过的相关知识进行说明?二、定理的引入及推导设线段AB的中点为P1,线段BC的三等分点为P2、P3.则:这时你想到了什么?AP1=P1B=BP2= P2P3= P3CDQ1=Q1E=EQ2=Q2Q3=Q3F平行线等分线段定理分别过点P1,P2, P3作直线a1,a2,a3平行于l1,与l? 的交点分别为Q1,Q2,Q3.ll? 1234平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例. 若将下图中的直线L2看成是平行于△ABC的边BC的直线,那么可得:推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.除此之外,还有其它对应线段成比例吗??反 比合 比合 比反 比合比三、定理的运用91、已知: L1∥L2∥L3 则:例1(一、基础题) 3、如图1:已知L1∥L2∥L3 ,
AB=3厘米,BC=2厘米,DF=4.5厘米.
则EF=( ),DE=( ).
4、如图2:△ABC中,DE ∥BC,如果AE :EC=7 :3,则DB :AB=( )1.82.73:10 (二、提高题:)
1、如图:EF∥AB,BF:FC= 5 :4,
AC=3厘米,则CE=( )2、已知在△ABC中,DE∥BC,EF∥DC,那么下列结论不成立的是( )3、如图: △ABC中, DE ∥BC,DF ∥AC,AE=4,EC=2,BC=8,求线段BF,CF之长.B 例2:三角形内角平分线分对边成两线段,这两线段和相邻的两边成比例.证明:作CE//DA交BA的延长线于E.∵CE//DA,∴∠1=∠4 ,∠2=∠3.又∵∠1=∠2(已知),∴∠3=∠4, ∴AC=AE .例3:用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.(文字语言)(图形语言)分析:由平行线分线段
成比例定理的推论可直
接得到AD:AB=AE:AC.为了证明AE:AC=DE:BC,
需要构造一组平行线,使
AE、AC、DE、BC成为
由这组平行线截得的线段.
故作EF//AB.证明:过点E作EF//AB,交BC于点F,
∵DE//BC, ∴AD:AB=AE:AC.
∵EF//AB, ∴BF:BC=AE:AC.
且四边形DEFB为平行四边形.
∴DE=BF.∴ DE:BC=AE:AC.已知:如图,DE//BC分别交AB、AC于点D、E.求证:
(图形语言)四 课后小结1、学习掌握平行线等分线段定理,了解定理的证明。
2、正确理解“对应线段成比例”,能正确写出需要的比例式。
了解平行线分线段成比例定理是一般情况,平行线等分线段定理的特殊情况,明确我们的研究是采用从特殊到一般的数学方法。
(注意其前提条件是:等距)三条距离不相等的平行线截两条直线会有什么结果?猜想:你能否利用所学过的相关知识进行说明?二、定理的引入及推导设线段AB的中点为P1,线段BC的三等分点为P2、P3.则:这时你想到了什么?AP1=P1B=BP2= P2P3= P3CDQ1=Q1E=EQ2=Q2Q3=Q3F平行线等分线段定理分别过点P1,P2, P3作直线a1,a2,a3平行于l1,与l? 的交点分别为Q1,Q2,Q3.ll? 1234平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例. 若将下图中的直线L2看成是平行于△ABC的边BC的直线,那么可得:推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.除此之外,还有其它对应线段成比例吗??反 比合 比合 比反 比合比三、定理的运用91、已知: L1∥L2∥L3 则:例1(一、基础题) 3、如图1:已知L1∥L2∥L3 ,
AB=3厘米,BC=2厘米,DF=4.5厘米.
则EF=( ),DE=( ).
4、如图2:△ABC中,DE ∥BC,如果AE :EC=7 :3,则DB :AB=( )1.82.73:10 (二、提高题:)
1、如图:EF∥AB,BF:FC= 5 :4,
AC=3厘米,则CE=( )2、已知在△ABC中,DE∥BC,EF∥DC,那么下列结论不成立的是( )3、如图: △ABC中, DE ∥BC,DF ∥AC,AE=4,EC=2,BC=8,求线段BF,CF之长.B 例2:三角形内角平分线分对边成两线段,这两线段和相邻的两边成比例.证明:作CE//DA交BA的延长线于E.∵CE//DA,∴∠1=∠4 ,∠2=∠3.又∵∠1=∠2(已知),∴∠3=∠4, ∴AC=AE .例3:用平行于三角形一边且和其他两边相交的直线截三角形,所截得的三角形的三边与原三角形的三边对应成比例.(文字语言)(图形语言)分析:由平行线分线段
成比例定理的推论可直
接得到AD:AB=AE:AC.为了证明AE:AC=DE:BC,
需要构造一组平行线,使
AE、AC、DE、BC成为
由这组平行线截得的线段.
故作EF//AB.证明:过点E作EF//AB,交BC于点F,
∵DE//BC, ∴AD:AB=AE:AC.
∵EF//AB, ∴BF:BC=AE:AC.
且四边形DEFB为平行四边形.
∴DE=BF.∴ DE:BC=AE:AC.已知:如图,DE//BC分别交AB、AC于点D、E.求证:
(图形语言)四 课后小结1、学习掌握平行线等分线段定理,了解定理的证明。
2、正确理解“对应线段成比例”,能正确写出需要的比例式。
了解平行线分线段成比例定理是一般情况,平行线等分线段定理的特殊情况,明确我们的研究是采用从特殊到一般的数学方法。
