选修4-1 第一讲 相似三角形的判定及有关性质 平行线等分线段定理 课件21张PPT
文档属性
| 名称 | 选修4-1 第一讲 相似三角形的判定及有关性质 平行线等分线段定理 课件21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 839.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 00:00:00 | ||
图片预览






文档简介
课件21张PPT。1.1 平行线等分线段定理1.理解平行线等分线段定理及推论.
2.掌握任意等分线段的方法.
3.能利用平行线等分线段定理解决简单几何问题.题型一 做线段的等分点 例1 已知线段AB,求作AB的五等分点.
分析:本题是平行线等分线段定理的实际应用.只要作射线AM,在AM上任意截取5条相等线段,设分别为AA1、A1A2、A2A3、A3A4、A4A5,连接端点A5与点B,再过其他端点作BA5的平行线,分别交AB于C、D、E、F,则AB就被这些平行线分成五等分了.
解析:(1)作射线AM.
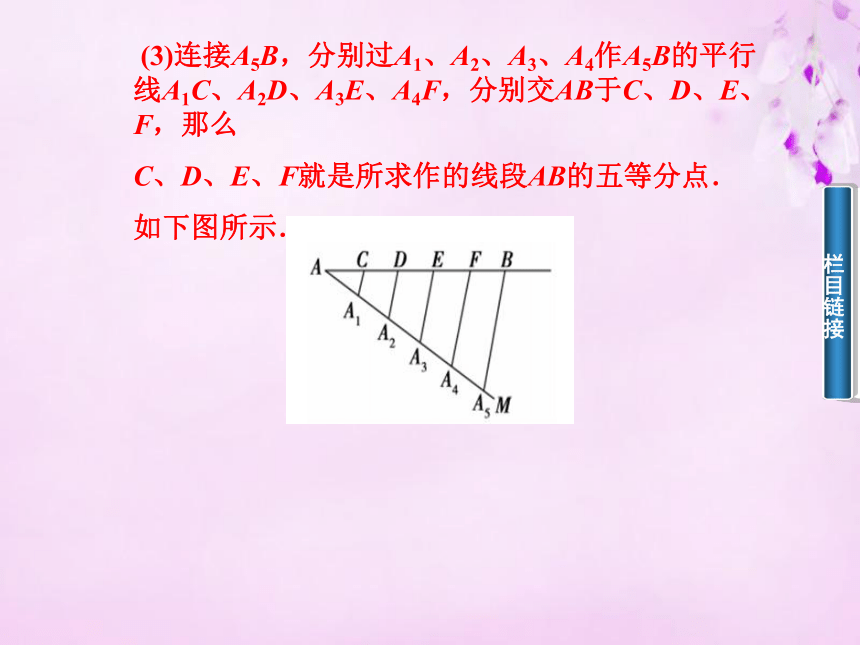
(2)在射线AM上截取AA1=A1A2=A2A3=A3A4=A4A5. (3)连接A5B,分别过A1、A2、A3、A4作A5B的平行线A1C、A2D、A3E、A4F,分别交AB于C、D、E、F,那么
C、D、E、F就是所求作的线段AB的五等分点.
如下图所示.
点评:求作已知线段AB的n等分点的一般作法:过线段AB的一个端点作一条射线,从射线的端点起,依次截取n条相等的线段,然后连接第n条线段的末端与已知线段的另一个端点,过射线上各个分点作所连线段的平行线,这些平行线与已知线段的交点就是线段AB的n等分点.?变式训练
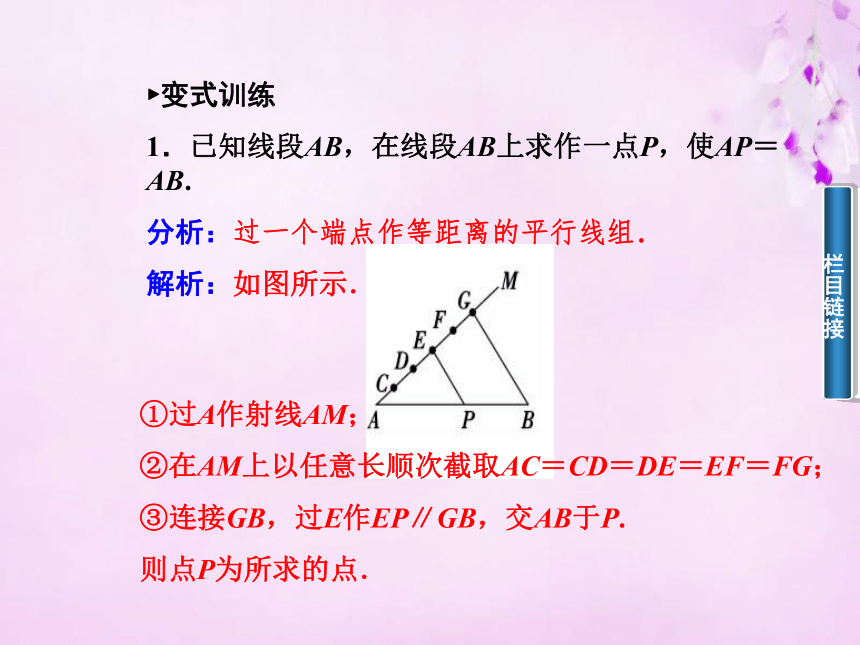
1.已知线段AB,在线段AB上求作一点P,使AP=AB.
分析:过一个端点作等距离的平行线组.
解析:如图所示.①过A作射线AM;
②在AM上以任意长顺次截取AC=CD=DE=EF=FG;
③连接GB,过E作EP∥GB,交AB于P.
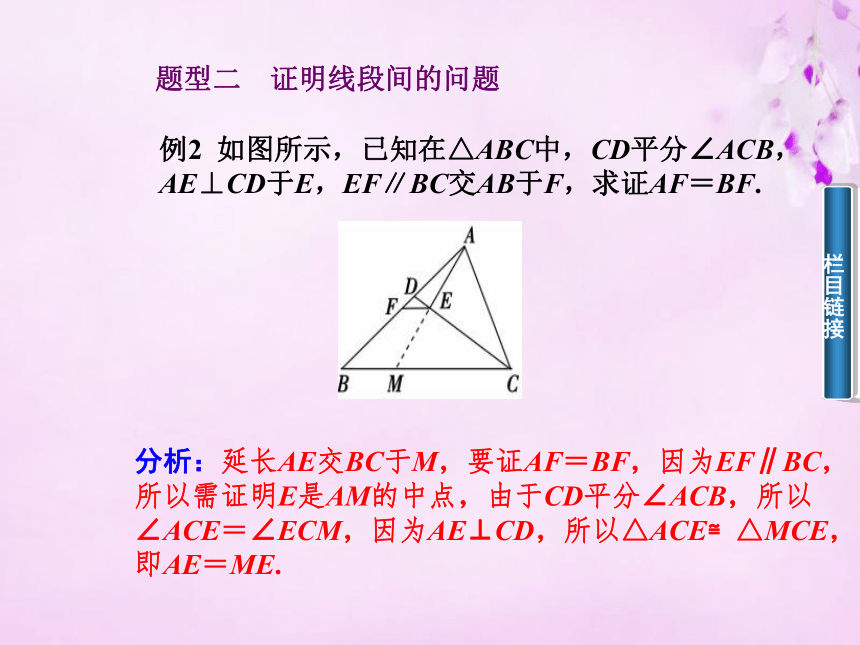
则点P为所求的点.题型二 证明线段间的问题例2 如图所示,已知在△ABC中,CD平分∠ACB,AE⊥CD于E,EF∥BC交AB于F,求证AF=BF.分析:延长AE交BC于M,要证AF=BF,因为EF∥BC,所以需证明E是AM的中点,由于CD平分∠ACB,所以∠ACE=∠ECM,因为AE⊥CD,所以△ACE≌△MCE,即AE=ME. 证明:延长AE交BC于M.
∵CD平分∠ACB,AE⊥CD于E,
∴在△ACE和△MCE中,
∠AEC=∠CEM,CE=CE,
∠ACD=∠MCD,
∴△ACE≌△MCE,
∴AE=EM,即E是AM的中点.
又在△ABM中,EF∥BM,AE=EM,
∴F是AB的中点,∴AF=BF.点评:在几何证明中添加辅助线的常见方法:①在三角形中,利用角平分线可构造全等三角形或相似三角形;②在三角形或梯形中,若已知一边或一腰的中点,则过中点可作平行于底边的辅助线.?变式训练
2.如图,已知在△ABC中,D是AC的中点,DE∥BC,交AB于点E,EF∥AC交BC于点F,求证:BF=CF.
分析:D是AC的中点,利用定理知E是AB的中点,再利用定理得F是BC的中点.
证明:在△ABC中,
∵D是AC的中点,DE∥BC,
∴E是AB的中点(推论1).
又∵EF∥AC且交BC于点F,
∴F是BC的中点(推论1).
∴BF=FC.
点评:应用定理证明线段间关系,常与三角形中位线、梯形中位线有关.题型三 求线段的长 点评:当题中出现中点条件时,常过中点作平行线,构造平分线等分线段定理及推论的基本图形解题.?变式训练
3.如图所示,在?ABCD中,对角线AC,BD相交于O,OE∥AB交BC于E,AD=6,求BE的长.析 疑 难 提 能 力例 如图所示,在△ABC中,∠ACB=90°,AC=BC,E,F分别在AC,BC上,且CE=CF,EM⊥AF交AB于M,CN⊥AF交AB于N,求证MN=NB.【错解】延长AF,过B作BD∥NC交AF的延长线于D.
∵EM⊥AF,CN⊥AF,∴EM∥CN.
又BD∥CN,∴BD∥CN∥ME,
∴BN=NM.
分析:“错解”中只说明了BD∥CN∥ME,而相邻两平行直线间的距离是否相等未说明,就认为BN=NM,这是不对的.
点评:本题是利用平行线等分线段定理求作已知线段的等分点.解决此类问题一般是先作一条射线,再截取题目所需的线段数,然后用平行线等分线段定理画图.【正解】如图所示,延长线ME交BC的延长线于点P,
由题意可得Rt△EPC≌Rt△FAC,∴PC=AC=BC.
又∵EM⊥AF,CN⊥AF,∴PM∥CN.
由题意知点C是BP的中点,∴点N是MB的中点,∴MN=NB.
【疑难点辨析】定理中的“一组平行线”是每相邻两条直线间的距离都相等的平行线,若不满足这一条件,则不能使用该定理.
2.掌握任意等分线段的方法.
3.能利用平行线等分线段定理解决简单几何问题.题型一 做线段的等分点 例1 已知线段AB,求作AB的五等分点.
分析:本题是平行线等分线段定理的实际应用.只要作射线AM,在AM上任意截取5条相等线段,设分别为AA1、A1A2、A2A3、A3A4、A4A5,连接端点A5与点B,再过其他端点作BA5的平行线,分别交AB于C、D、E、F,则AB就被这些平行线分成五等分了.
解析:(1)作射线AM.
(2)在射线AM上截取AA1=A1A2=A2A3=A3A4=A4A5. (3)连接A5B,分别过A1、A2、A3、A4作A5B的平行线A1C、A2D、A3E、A4F,分别交AB于C、D、E、F,那么
C、D、E、F就是所求作的线段AB的五等分点.
如下图所示.
点评:求作已知线段AB的n等分点的一般作法:过线段AB的一个端点作一条射线,从射线的端点起,依次截取n条相等的线段,然后连接第n条线段的末端与已知线段的另一个端点,过射线上各个分点作所连线段的平行线,这些平行线与已知线段的交点就是线段AB的n等分点.?变式训练
1.已知线段AB,在线段AB上求作一点P,使AP=AB.
分析:过一个端点作等距离的平行线组.
解析:如图所示.①过A作射线AM;
②在AM上以任意长顺次截取AC=CD=DE=EF=FG;
③连接GB,过E作EP∥GB,交AB于P.
则点P为所求的点.题型二 证明线段间的问题例2 如图所示,已知在△ABC中,CD平分∠ACB,AE⊥CD于E,EF∥BC交AB于F,求证AF=BF.分析:延长AE交BC于M,要证AF=BF,因为EF∥BC,所以需证明E是AM的中点,由于CD平分∠ACB,所以∠ACE=∠ECM,因为AE⊥CD,所以△ACE≌△MCE,即AE=ME. 证明:延长AE交BC于M.
∵CD平分∠ACB,AE⊥CD于E,
∴在△ACE和△MCE中,
∠AEC=∠CEM,CE=CE,
∠ACD=∠MCD,
∴△ACE≌△MCE,
∴AE=EM,即E是AM的中点.
又在△ABM中,EF∥BM,AE=EM,
∴F是AB的中点,∴AF=BF.点评:在几何证明中添加辅助线的常见方法:①在三角形中,利用角平分线可构造全等三角形或相似三角形;②在三角形或梯形中,若已知一边或一腰的中点,则过中点可作平行于底边的辅助线.?变式训练
2.如图,已知在△ABC中,D是AC的中点,DE∥BC,交AB于点E,EF∥AC交BC于点F,求证:BF=CF.
分析:D是AC的中点,利用定理知E是AB的中点,再利用定理得F是BC的中点.
证明:在△ABC中,
∵D是AC的中点,DE∥BC,
∴E是AB的中点(推论1).
又∵EF∥AC且交BC于点F,
∴F是BC的中点(推论1).
∴BF=FC.
点评:应用定理证明线段间关系,常与三角形中位线、梯形中位线有关.题型三 求线段的长 点评:当题中出现中点条件时,常过中点作平行线,构造平分线等分线段定理及推论的基本图形解题.?变式训练
3.如图所示,在?ABCD中,对角线AC,BD相交于O,OE∥AB交BC于E,AD=6,求BE的长.析 疑 难 提 能 力例 如图所示,在△ABC中,∠ACB=90°,AC=BC,E,F分别在AC,BC上,且CE=CF,EM⊥AF交AB于M,CN⊥AF交AB于N,求证MN=NB.【错解】延长AF,过B作BD∥NC交AF的延长线于D.
∵EM⊥AF,CN⊥AF,∴EM∥CN.
又BD∥CN,∴BD∥CN∥ME,
∴BN=NM.
分析:“错解”中只说明了BD∥CN∥ME,而相邻两平行直线间的距离是否相等未说明,就认为BN=NM,这是不对的.
点评:本题是利用平行线等分线段定理求作已知线段的等分点.解决此类问题一般是先作一条射线,再截取题目所需的线段数,然后用平行线等分线段定理画图.【正解】如图所示,延长线ME交BC的延长线于点P,
由题意可得Rt△EPC≌Rt△FAC,∴PC=AC=BC.
又∵EM⊥AF,CN⊥AF,∴PM∥CN.
由题意知点C是BP的中点,∴点N是MB的中点,∴MN=NB.
【疑难点辨析】定理中的“一组平行线”是每相邻两条直线间的距离都相等的平行线,若不满足这一条件,则不能使用该定理.
