选修4-1 第一讲 相似三角形的判定及有关性质 直角三角形的射影定理 课件20张PPT
文档属性
| 名称 | 选修4-1 第一讲 相似三角形的判定及有关性质 直角三角形的射影定理 课件20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:23:52 | ||
图片预览







文档简介
课件20张PPT。高中数学人教A版选修4-1
第一章 第四节
直角三角形的射影定理
1.射影
(1)点在直线上的正射影:从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的正射影.
(2)线段在直线上的正射影:一条线段的两个端点在一条直线上的正射影之间的线段,叫做这条线段在这条直线上的正射影.
(3)射影:点和线段的正射影简称为射影.【做一做1】 如图,AD⊥BC,EF⊥BC,垂足分别为点D,E.指出点A,B,C,D,E,F,G和线段AB,AC,AF,FG在直线BC上的射影.
?
解:由AD⊥BC,EF⊥BC可知,点A在直线BC上的射影是点D;点B在直线BC上的射影是点B,点C在直线BC上的射影是点C,点D在直线BC上的射影是点D,点E,F,G在直线BC上的射影都是点E;线段AB在直线BC上的射影是DB,线段AC在直线BC上的射影是DC,线段AF在直线BC上的射影是DE,线段FG在直线BC上的射影是点E.2.直角三角形的射影定理
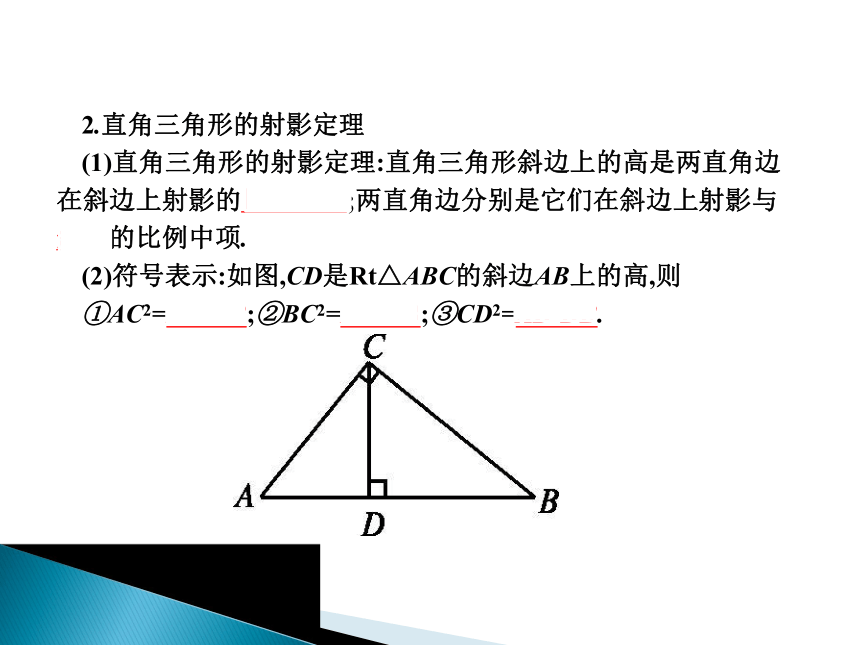
(1)直角三角形的射影定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.
(2)符号表示:如图,CD是Rt△ABC的斜边AB上的高,则
①AC2=AD·AB;②BC2=BD·AB;③CD2=AD·DB.名师点拨1.应用射影定理的条件
(1)三角形是直角三角形;(2)给出直角三角形斜边上的高.
2.射影定理的逆定理仍然成立.
如果一个三角形一边上的高是另两边在这条边上的射影的比例中项,那么这个三角形是直角三角形.
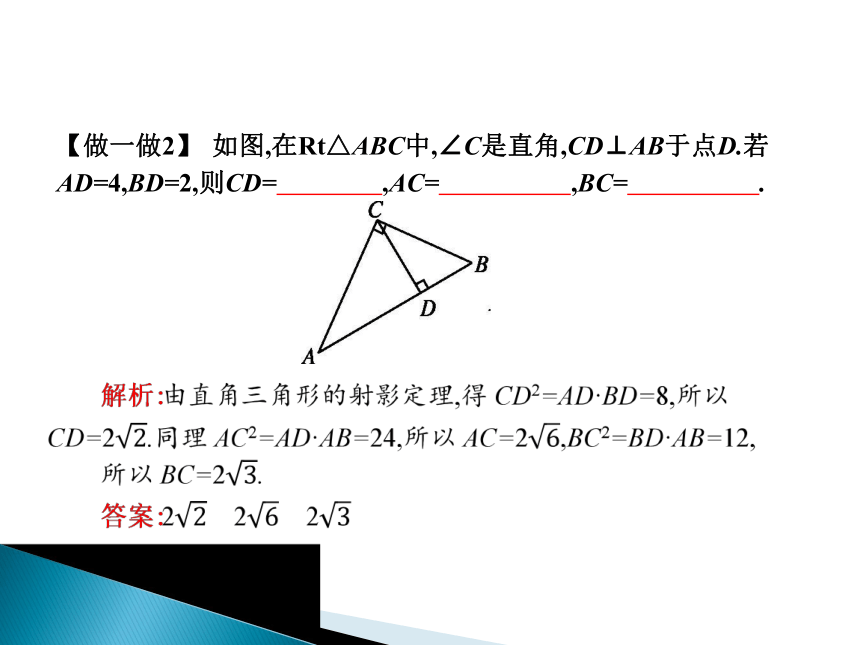
符号表示:如图,在△ABC中,CD⊥AB于点D.若CD2=AD·BD,则△ABC为直角三角形.【做一做2】 如图,在Rt△ABC中,∠C是直角,CD⊥AB于点D.若AD=4,BD=2,则CD= ,AC= ,BC= .?思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)一条线段的射影不可能是点. ( )
(2)在Rt△ABC中,∠C是直角,CD⊥AB于点D,则AD2=AC·AB. ( )
(3)如果一个三角形一边上的高是另两边在这条边上的射影的比例中项,那么这个三角形是直角三角形. ( )
答案:(1)× (2)× (3)√探究一探究二探究三思维辨析当堂检测利用射影定理解决计算问题
【例1】 如图,D为△ABC中BC边上的一点,∠CAD=∠B.若AD=6, AB=10,BD=8,求CD的长.
分析:由条件知∠ADB=90°,即AD⊥BC,进一步可得∠BAC=90°,由射影定理求CD的长.
解:在△ABD中,AD=6,AB=10,BD=8,满足AB2=AD2+BD2,
故∠ADB=90°,即AD⊥BC.
∵∠CAD=∠B,且∠C+∠CAD=90°,
∴∠C+∠B=90°,
∴∠BAC=90°.
在Rt△BAC中,AD⊥BC,由射影定理可知,AD2=BD·CD,即62=8CD,故CD= .探究一探究二探究三思维辨析当堂检测反思感悟利用直角三角形的射影定理解决计算问题时,首先要创造应用射影定理的条件,即构造直角三角形或垂直关系,然后再对照射影定理建立线段长度之间的等量关系,最后通过解方程求得相应线段的长度.探究一探究二探究三思维辨析当堂检测答案:A 探究一探究二探究三思维辨析当堂检测利用射影定理解决证明问题
【例2】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,DF⊥AC于点F,DE⊥AB于点E.证明:
(1)AB·AC=AD·BC;
(2)AD3=BC·BE·CF.
分析:(1)可针对△ABC的面积利用等积法证得;(2)在Rt△BAC中,有AB·AC=AD·BC,AD2=BD·DC;在Rt△ADB中,有BD2=BE·AB;在Rt△ADC中,有CD2=CF·AC.由这些关系式便可得到待证式.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测反思感悟利用直角三角形的射影定理证明恒等式
(1)结合图形,仔细分析题目的结论;
(2)由于射影定理中可供选择的等式较多,需要合理选择.探究一探究二探究三思维辨析当堂检测变式训练2如图,CD垂直平分AB,点E在CD上,DF⊥AC于点F, DG⊥BE于点G.求证:AF·AC=BG·BE.
?
证明:∵CD垂直平分AB,
∴△ACD和△BED均为直角三角形,且AD=DB.
又DF⊥AC,DG⊥BE,
∴AD2=AF·AC,DB2=BG·BE,
∴AF·AC=BG·BE.探究一探究二探究三思维辨析当堂检测1.一条线段在某条直线上的射影不可能是( )
A.点
B.线段
C.直线
D.与该线段重合的一条线段
解析:线段在任何直线上的射影都不可能是直线.
答案:C
2.在Rt△ABC中,∠A=90°,AD⊥BC于点D.若DC·DB=9,则AD=( )
A.9 B.3 C.3 D.18
解析:由射影定理,得AD2=DC·DB=9,解得AD=3.
答案:B探究一探究二探究三思维辨析当堂检测3.在Rt△ACB中,∠C=90°,CD⊥AB于点D.若BD∶AD=1∶4,则tan∠BCD的值是( )解析: 答案:C 探究一探究二探究三思维辨析当堂检测4.在一直角三角形中,斜边上的高为6 cm,且把斜边分成3∶2两段,则斜边上中线的长是 .?探究一探究二探究三思维辨析当堂检测5.如图,已知CD是Rt△ACB斜边AB上的高,AC∶BC=3∶4.
(1)计算AD∶BD的值;
(2)若AB=25,求CD的长.
解:(1)∵AC2=AD·AB,BC2=BD·AB,作业:1.课本22页习题1.4 2.同步习题(四)
直角三角形的射影定理
1.射影
(1)点在直线上的正射影:从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的正射影.
(2)线段在直线上的正射影:一条线段的两个端点在一条直线上的正射影之间的线段,叫做这条线段在这条直线上的正射影.
(3)射影:点和线段的正射影简称为射影.【做一做1】 如图,AD⊥BC,EF⊥BC,垂足分别为点D,E.指出点A,B,C,D,E,F,G和线段AB,AC,AF,FG在直线BC上的射影.
?
解:由AD⊥BC,EF⊥BC可知,点A在直线BC上的射影是点D;点B在直线BC上的射影是点B,点C在直线BC上的射影是点C,点D在直线BC上的射影是点D,点E,F,G在直线BC上的射影都是点E;线段AB在直线BC上的射影是DB,线段AC在直线BC上的射影是DC,线段AF在直线BC上的射影是DE,线段FG在直线BC上的射影是点E.2.直角三角形的射影定理
(1)直角三角形的射影定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.
(2)符号表示:如图,CD是Rt△ABC的斜边AB上的高,则
①AC2=AD·AB;②BC2=BD·AB;③CD2=AD·DB.名师点拨1.应用射影定理的条件
(1)三角形是直角三角形;(2)给出直角三角形斜边上的高.
2.射影定理的逆定理仍然成立.
如果一个三角形一边上的高是另两边在这条边上的射影的比例中项,那么这个三角形是直角三角形.
符号表示:如图,在△ABC中,CD⊥AB于点D.若CD2=AD·BD,则△ABC为直角三角形.【做一做2】 如图,在Rt△ABC中,∠C是直角,CD⊥AB于点D.若AD=4,BD=2,则CD= ,AC= ,BC= .?思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)一条线段的射影不可能是点. ( )
(2)在Rt△ABC中,∠C是直角,CD⊥AB于点D,则AD2=AC·AB. ( )
(3)如果一个三角形一边上的高是另两边在这条边上的射影的比例中项,那么这个三角形是直角三角形. ( )
答案:(1)× (2)× (3)√探究一探究二探究三思维辨析当堂检测利用射影定理解决计算问题
【例1】 如图,D为△ABC中BC边上的一点,∠CAD=∠B.若AD=6, AB=10,BD=8,求CD的长.
分析:由条件知∠ADB=90°,即AD⊥BC,进一步可得∠BAC=90°,由射影定理求CD的长.
解:在△ABD中,AD=6,AB=10,BD=8,满足AB2=AD2+BD2,
故∠ADB=90°,即AD⊥BC.
∵∠CAD=∠B,且∠C+∠CAD=90°,
∴∠C+∠B=90°,
∴∠BAC=90°.
在Rt△BAC中,AD⊥BC,由射影定理可知,AD2=BD·CD,即62=8CD,故CD= .探究一探究二探究三思维辨析当堂检测反思感悟利用直角三角形的射影定理解决计算问题时,首先要创造应用射影定理的条件,即构造直角三角形或垂直关系,然后再对照射影定理建立线段长度之间的等量关系,最后通过解方程求得相应线段的长度.探究一探究二探究三思维辨析当堂检测答案:A 探究一探究二探究三思维辨析当堂检测利用射影定理解决证明问题
【例2】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,DF⊥AC于点F,DE⊥AB于点E.证明:
(1)AB·AC=AD·BC;
(2)AD3=BC·BE·CF.
分析:(1)可针对△ABC的面积利用等积法证得;(2)在Rt△BAC中,有AB·AC=AD·BC,AD2=BD·DC;在Rt△ADB中,有BD2=BE·AB;在Rt△ADC中,有CD2=CF·AC.由这些关系式便可得到待证式.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测反思感悟利用直角三角形的射影定理证明恒等式
(1)结合图形,仔细分析题目的结论;
(2)由于射影定理中可供选择的等式较多,需要合理选择.探究一探究二探究三思维辨析当堂检测变式训练2如图,CD垂直平分AB,点E在CD上,DF⊥AC于点F, DG⊥BE于点G.求证:AF·AC=BG·BE.
?
证明:∵CD垂直平分AB,
∴△ACD和△BED均为直角三角形,且AD=DB.
又DF⊥AC,DG⊥BE,
∴AD2=AF·AC,DB2=BG·BE,
∴AF·AC=BG·BE.探究一探究二探究三思维辨析当堂检测1.一条线段在某条直线上的射影不可能是( )
A.点
B.线段
C.直线
D.与该线段重合的一条线段
解析:线段在任何直线上的射影都不可能是直线.
答案:C
2.在Rt△ABC中,∠A=90°,AD⊥BC于点D.若DC·DB=9,则AD=( )
A.9 B.3 C.3 D.18
解析:由射影定理,得AD2=DC·DB=9,解得AD=3.
答案:B探究一探究二探究三思维辨析当堂检测3.在Rt△ACB中,∠C=90°,CD⊥AB于点D.若BD∶AD=1∶4,则tan∠BCD的值是( )解析: 答案:C 探究一探究二探究三思维辨析当堂检测4.在一直角三角形中,斜边上的高为6 cm,且把斜边分成3∶2两段,则斜边上中线的长是 .?探究一探究二探究三思维辨析当堂检测5.如图,已知CD是Rt△ACB斜边AB上的高,AC∶BC=3∶4.
(1)计算AD∶BD的值;
(2)若AB=25,求CD的长.
解:(1)∵AC2=AD·AB,BC2=BD·AB,作业:1.课本22页习题1.4 2.同步习题(四)
