选修4-1 第一讲 相似三角形的判定及有关性质 直角三角形的射影定理课件21张PPT
文档属性
| 名称 | 选修4-1 第一讲 相似三角形的判定及有关性质 直角三角形的射影定理课件21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 552.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:22:27 | ||
图片预览





文档简介
课件21张PPT。四 直角三角形的射影定理主讲人:王娟 影子与我们的生活息息相关。如果没有影子的话我们的生活不知道会是怎么样的一个样子?四 直角三角形的射影定理一.复习
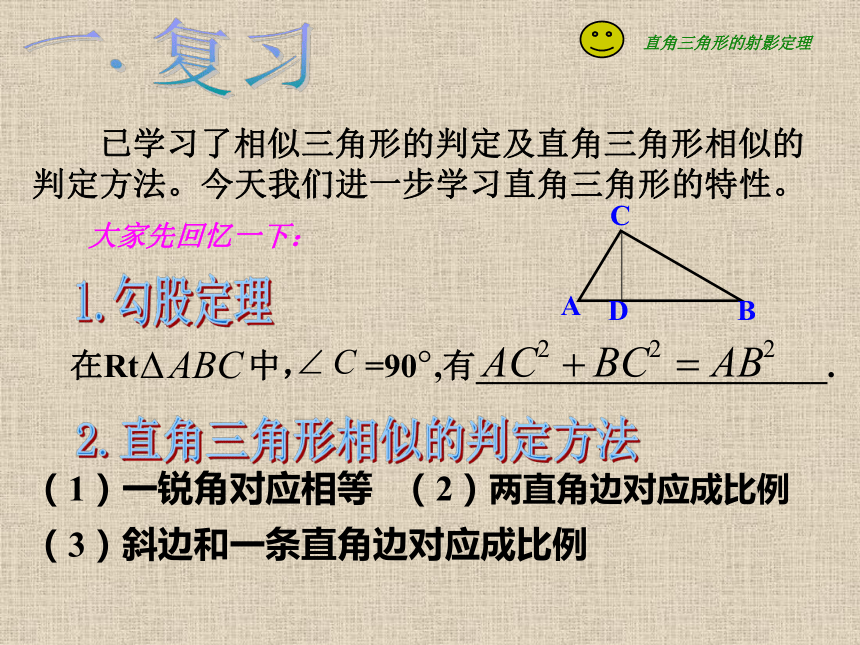
已学习了相似三角形的判定及直角三角形相似的判定方法。今天我们进一步学习直角三角形的特性。1.勾股定理2.直角三角形相似的判定方法(1)一锐角对应相等 (2)两直角边对应成比例
(3)斜边和一条直角边对应成比例大家先回忆一下:探究:如图,△ABC是直角三角形,CD为斜边AB上的高。在这个图形中,由于线段AD与CD、BD与CD、BC与AC等相互垂直。你能发现这些线段之间的某些关系吗?∵∠1=90°-∠2,
∠B=90°-∠2,∴∠B=∠1 ∴△ACD∽△CBD∴AD:CD=CD:BD 即CD2 =AD·BD (1) ∵∠B是公共角 ∴△BDC∽△BCA
∴BD:BC=BC:AB 即BC2 =BD ·AB (2)
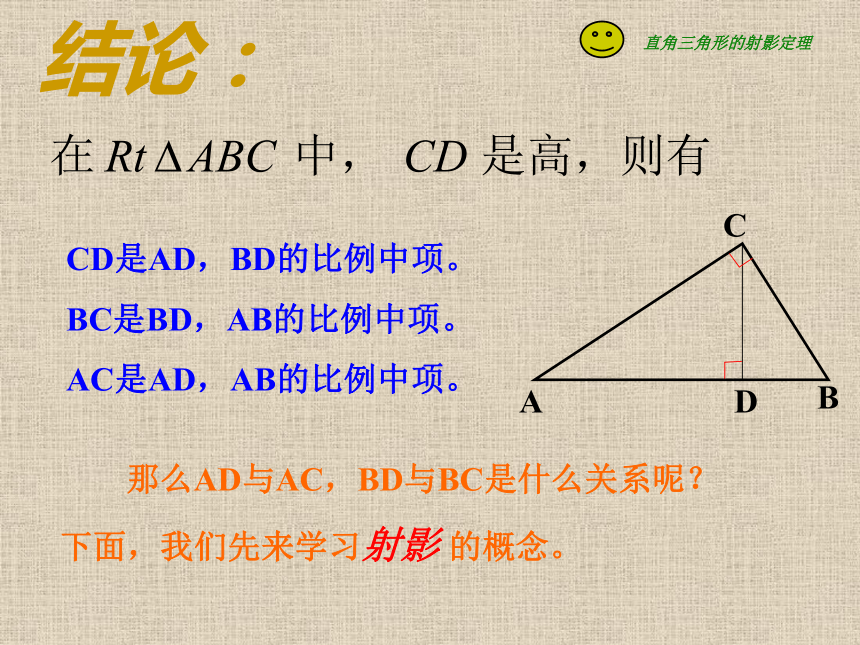
同理,由△CDA∽△BCA,有AC2 =AD· AB (3)提示:通过寻找图形中的相似三角形来探究这些线段间的关系考察RT△BDC和RT△BCA考察RT△ACD和RT△CBDCD是AD,BD的比例中项。
BC是BD,AB的比例中项。
AC是AD,AB的比例中项。 那么AD与AC,BD与BC是什么关系呢?
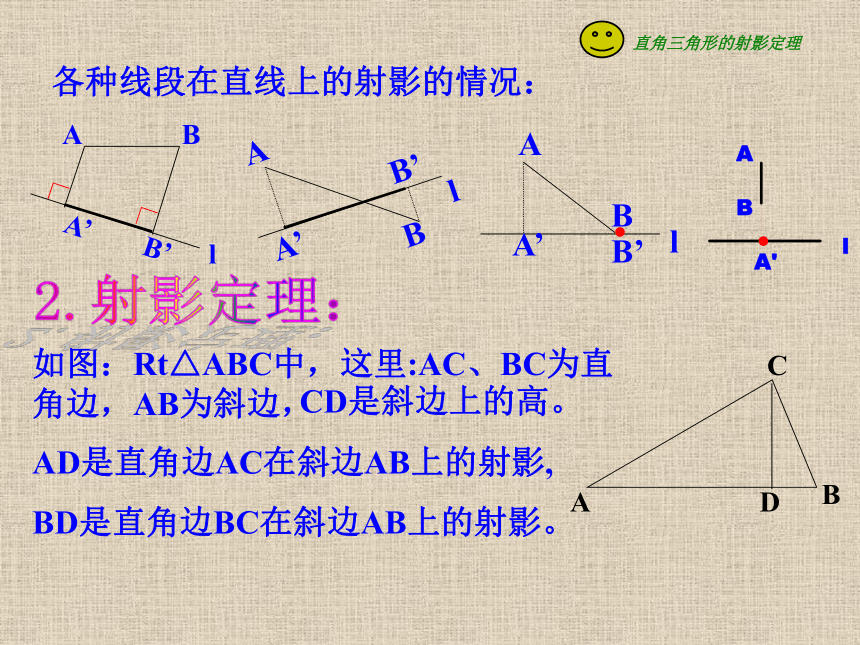
下面,我们先来学习射影 的概念。结论: 影子与我们的生活息息相关。如果没有影子的话,我们的生活不知道会是怎么样的?二.新课1.射影: (1)太阳光垂直照在A点,留在直线MN上的影子应是什么?(2)线段AB留在MN上的影子是什么?定义:点A'线段A'B'(1)从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的正射影。(2)一条线段在直线上的正射影,是指线段的两个端点在这条直线上的正射影间的线段。(即垂足间的线段)注意:点和线段的正射影简称为射影··B’各种线段在直线上的射影的情况:如图:Rt△ABC中,这里:AC、BC为直角边,AB为斜边,CD是斜边上的高。AD是直角边AC在斜边AB上的射影,
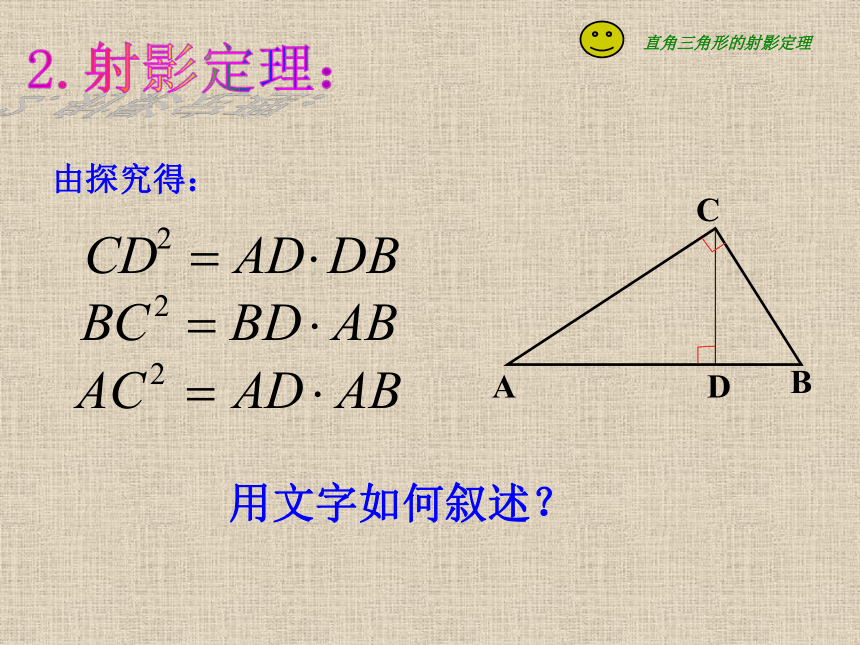
BD是直角边BC在斜边AB上的射影。2.射影定理:ABA’.l2.射影定理:用文字如何叙述? 直角三角形斜边上的高是两直角边在斜边上射影的比例中项;
两直角边分别是它们在斜边上的射影与斜边的比例中项.2.射影定理:具体题目运用:3.应用AC2=AD·AB=2×10=20,解得AC=2
∵∠ACB是半圆上的圆周角
∴∠ACB=90°,即△ABC是直角三角形BC2=BD·AB=8×10=80,解得BC=8
解:分析:利用射影定理和勾股定理又CD为斜边上的高,由射影定理可得CD2=AD·BD=2×8=16,解得CD=4
强调:射影定理只能用在直角三角形中,且必须
有斜边上的高例1:如图,圆O上一点C在直径AB上的射影为D,若AD=2,DB=8,求CD、AC和BC的长。这里犯迷糊可不行!28课堂练习:P22 1、在△ABC中,∠C=90°,CD是斜边AB上的高,已知CD=60,AD=25,求BD、AB、AC、BC的长。参考答案:BD=144
AB=169
AC=65
BC=156小结: (1)在 中,CD为斜边AB上的高,图中共有6条线段AC,BC,CD,AD,DB,AB已知任意两条,便可求出其余四条. (2)射影定理中每个乘积式中,含三条线段,若已知两条可求第三条.
(3)解题过程中,注意和勾股定理联系,选择简便方法.要么找角, 要么找边.例2.如图,△ABC中,顶点C在AB边上的射影为D,且CD 2 =AD· DB,求证:△ABC是直角三角形。分析:欲证∠ACB=90°即证∠1+∠2=90°已具备∠1+∠3=90°(?)只需∠2=∠3只需△BCD∽△CAD(∠B=∠1)()AD:CD=CD:DB垂直例2.如图,△ABC中,顶点C在AB边上的射影为D,
且CD2 =AD · DB,求证:△ABC是直角三角形。证明:在△CDA和△BDC中,
∵点C在AB上的射影为D,∴CD⊥AB
∴∠CDA=∠BDC=90°又∵CD2=AD ·DB
∴AD:CD=CD:DB∴△BCD∽△CAD∴∠2=∠3在△ACD中,∵∠1+∠3=90° ∴∠1+∠2=90°即∠ACB=90°∴△ABC是直角三角形
课本P22课堂练习:本节课小结:
如图中共有6条线段,已知任意2条,求其余线段。射影定理:运用射影定理时,注意前提条件求边注意联系方程与勾股定理不要忘了
哦!!作业:
P26、2
思考:如何用勾股定理证明射影定理?谢谢!再见!
已学习了相似三角形的判定及直角三角形相似的判定方法。今天我们进一步学习直角三角形的特性。1.勾股定理2.直角三角形相似的判定方法(1)一锐角对应相等 (2)两直角边对应成比例
(3)斜边和一条直角边对应成比例大家先回忆一下:探究:如图,△ABC是直角三角形,CD为斜边AB上的高。在这个图形中,由于线段AD与CD、BD与CD、BC与AC等相互垂直。你能发现这些线段之间的某些关系吗?∵∠1=90°-∠2,
∠B=90°-∠2,∴∠B=∠1 ∴△ACD∽△CBD∴AD:CD=CD:BD 即CD2 =AD·BD (1) ∵∠B是公共角 ∴△BDC∽△BCA
∴BD:BC=BC:AB 即BC2 =BD ·AB (2)
同理,由△CDA∽△BCA,有AC2 =AD· AB (3)提示:通过寻找图形中的相似三角形来探究这些线段间的关系考察RT△BDC和RT△BCA考察RT△ACD和RT△CBDCD是AD,BD的比例中项。
BC是BD,AB的比例中项。
AC是AD,AB的比例中项。 那么AD与AC,BD与BC是什么关系呢?
下面,我们先来学习射影 的概念。结论: 影子与我们的生活息息相关。如果没有影子的话,我们的生活不知道会是怎么样的?二.新课1.射影: (1)太阳光垂直照在A点,留在直线MN上的影子应是什么?(2)线段AB留在MN上的影子是什么?定义:点A'线段A'B'(1)从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的正射影。(2)一条线段在直线上的正射影,是指线段的两个端点在这条直线上的正射影间的线段。(即垂足间的线段)注意:点和线段的正射影简称为射影··B’各种线段在直线上的射影的情况:如图:Rt△ABC中,这里:AC、BC为直角边,AB为斜边,CD是斜边上的高。AD是直角边AC在斜边AB上的射影,
BD是直角边BC在斜边AB上的射影。2.射影定理:ABA’.l2.射影定理:用文字如何叙述? 直角三角形斜边上的高是两直角边在斜边上射影的比例中项;
两直角边分别是它们在斜边上的射影与斜边的比例中项.2.射影定理:具体题目运用:3.应用AC2=AD·AB=2×10=20,解得AC=2
∵∠ACB是半圆上的圆周角
∴∠ACB=90°,即△ABC是直角三角形BC2=BD·AB=8×10=80,解得BC=8
解:分析:利用射影定理和勾股定理又CD为斜边上的高,由射影定理可得CD2=AD·BD=2×8=16,解得CD=4
强调:射影定理只能用在直角三角形中,且必须
有斜边上的高例1:如图,圆O上一点C在直径AB上的射影为D,若AD=2,DB=8,求CD、AC和BC的长。这里犯迷糊可不行!28课堂练习:P22 1、在△ABC中,∠C=90°,CD是斜边AB上的高,已知CD=60,AD=25,求BD、AB、AC、BC的长。参考答案:BD=144
AB=169
AC=65
BC=156小结: (1)在 中,CD为斜边AB上的高,图中共有6条线段AC,BC,CD,AD,DB,AB已知任意两条,便可求出其余四条. (2)射影定理中每个乘积式中,含三条线段,若已知两条可求第三条.
(3)解题过程中,注意和勾股定理联系,选择简便方法.要么找角, 要么找边.例2.如图,△ABC中,顶点C在AB边上的射影为D,且CD 2 =AD· DB,求证:△ABC是直角三角形。分析:欲证∠ACB=90°即证∠1+∠2=90°已具备∠1+∠3=90°(?)只需∠2=∠3只需△BCD∽△CAD(∠B=∠1)()AD:CD=CD:DB垂直例2.如图,△ABC中,顶点C在AB边上的射影为D,
且CD2 =AD · DB,求证:△ABC是直角三角形。证明:在△CDA和△BDC中,
∵点C在AB上的射影为D,∴CD⊥AB
∴∠CDA=∠BDC=90°又∵CD2=AD ·DB
∴AD:CD=CD:DB∴△BCD∽△CAD∴∠2=∠3在△ACD中,∵∠1+∠3=90° ∴∠1+∠2=90°即∠ACB=90°∴△ABC是直角三角形
课本P22课堂练习:本节课小结:
如图中共有6条线段,已知任意2条,求其余线段。射影定理:运用射影定理时,注意前提条件求边注意联系方程与勾股定理不要忘了
哦!!作业:
P26、2
思考:如何用勾股定理证明射影定理?谢谢!再见!
