选修4-1 第一讲 相似三角形的判定及有关性质 相似三角形的判定及有关性质(第一课时)课件16张PPT
文档属性
| 名称 | 选修4-1 第一讲 相似三角形的判定及有关性质 相似三角形的判定及有关性质(第一课时)课件16张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 974.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 00:00:00 | ||
图片预览


文档简介
课件16张PPT。第一讲:相似三角形的判定
及有关性质教学
目标1.通过自学与交流,理解平行线等分线段定理、平行线分线段成比例定理、相似三角形的判定及有关性质及直角三角形的射影定理
2.数形结合理解平行线等分线段定理、平行线分线段成比例定理、相似三角形的判定及有关性质及直角三角形的射影定理的用途、用法,会用它们解决一些简单问题。重点
难点重点:探究、理解定理、性质,会用它们解决一些简单问题;
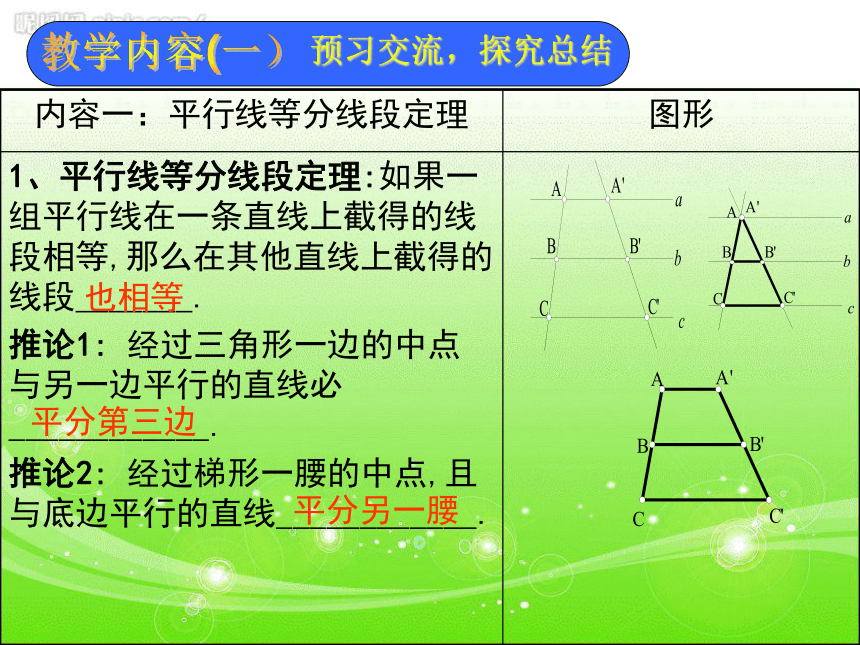
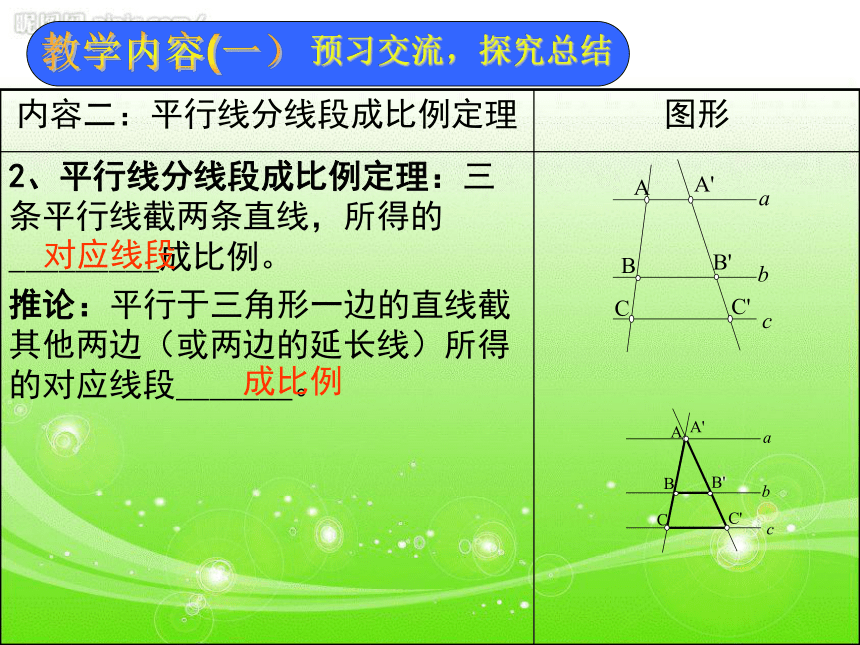
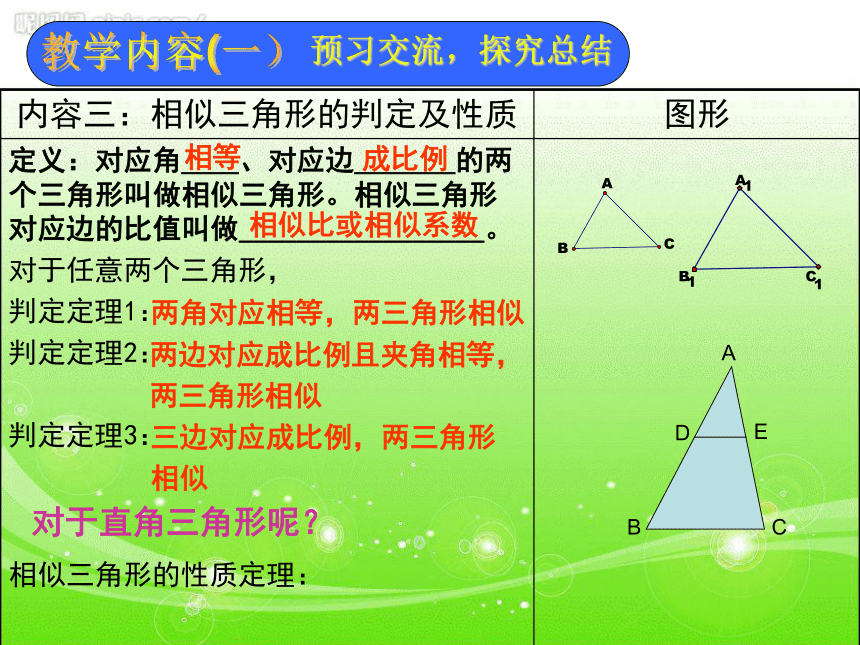
难点:会用定理、性质解决一些简单问题;教学内容(一)预习交流,探究总结也相等平分第三边平分另一腰教学内容(一)预习交流,探究总结对应线段成比例教学内容(一)预习交流,探究总结相等成比例相似比或相似系数两角对应相等,两三角形相似两边对应成比例且夹角相等,
两三角形相似三边对应成比例,两三角形
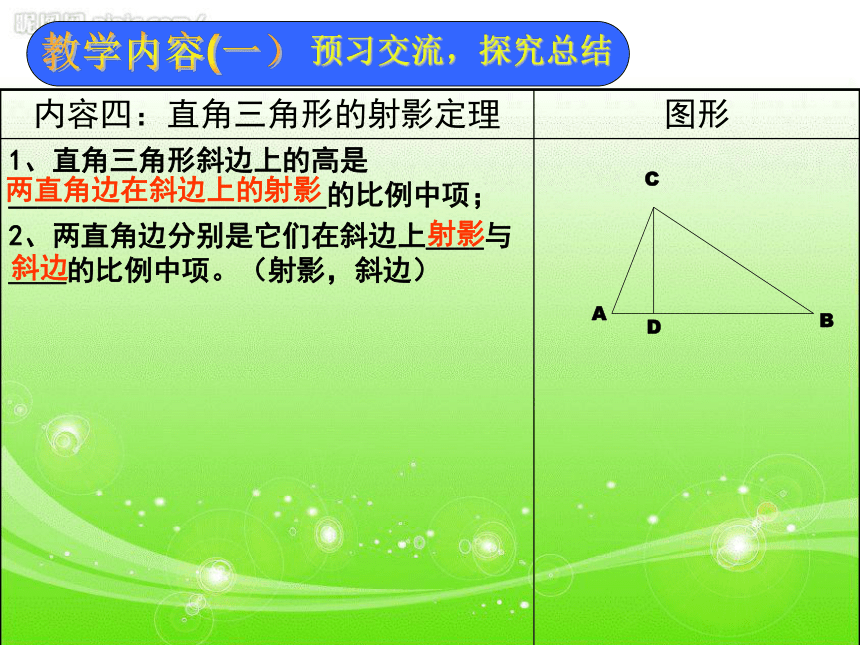
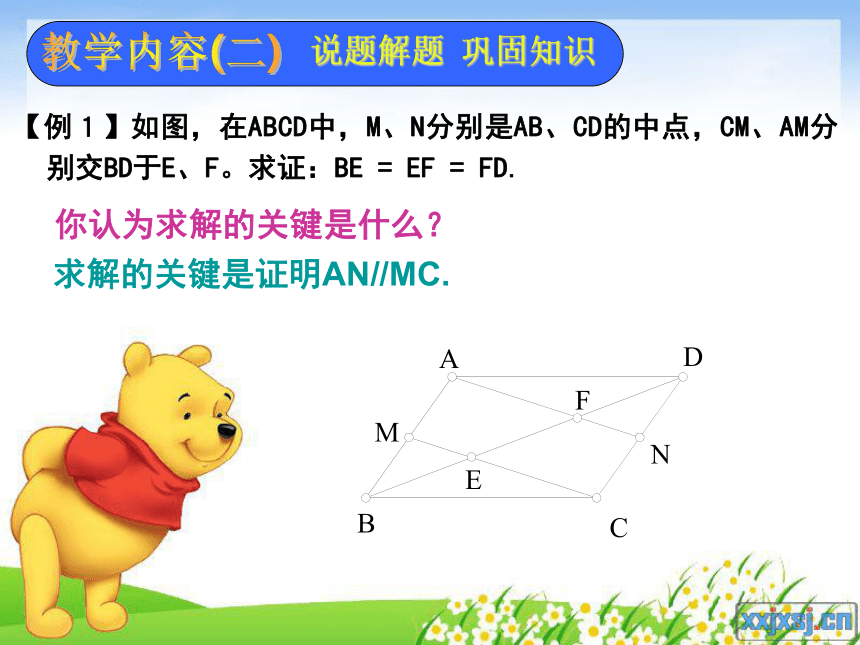
相似对于直角三角形呢?教学内容(一)预习交流,探究总结两直角边在斜边上的射影射影斜边教学内容(二)说题解题 巩固知识【例1】如图,在ABCD中,M、N分别是AB、CD的中点,CM、AM分别交BD于E、F。求证:BE = EF = FD. t你认为求解的关键是什么?求解的关键是证明AN//MC.教学内容(二)说题解题 巩固知识【例2】△ABC中,DE∥BC,F是BC上一点。AF交DE于点G,
AD:BD=2:1,BC=8.4cm。求(1)DE的长;(2) ;(3) . t你认为求解的关键是什么?求解的关键是利用平行DE//BC.教学内容(二)说题解题 巩固知识【例3】已知:如图,△ABC 的高AD、BE交于点F.求证:
(1)AD?BC=BE?AC;(2)AF?FD=BF?FE. t你认为求解的关键是什么?求解的关键是乘积关系→比例
关系→相似三角形.教学内容(二)说题解题 巩固知识【例4】如图,圆内接△ABC的角平分线CD延长后交圆于一点E.求证:EB?CB=CE?BD.t在圆中求解问题注意利用“等弧对等角”求解的关键是乘积关系→比例
关系→相似三角形.教学内容(二)说题解题 巩固知识【例5】如图,在△ABC内任取一点D,连接AD和BD.点E在△ABC外,∠EBC=∠ABD,∠ECB=∠DAB.求证: △DBE∽△ABC.t已知与所求要相互结合分析解题思路题后小结 知能提升1、抓住平行这一关键,构造相似(全等)三角形(或比例关系);
2、(乘积→)比例关系→相似(全等)三角形(或平行)。
3、线段长→三角形→相似(全等)三角形(相似三角形→比例关系→线段长)。1、如图,在△ABC中,D是AB的中点,DE//BC交AC于E,EF//AB交BC于F。
(1)求证:BF=CF;
(2)图中与DE相等的线段有________;
(3)图中与EF相等的线段有_________;
(4)若连结DF,则DF与AC的位置关系是_______,数量关系是_______. 教学内容(三)跟进练习 强化知识2、如图:⊿APM中,AM∥BN,CM∥DN,
求证:PA:PB=PC:PD. 教学内容(三)跟进练习 强化知识3、已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC?BC=BE?CD;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.教学内容(四)高考模拟 身临其境1、(2008梅州一模文)如图,在四边形ABCD中,E为AB中点,EF//BC,FG//AD,则 _____.
2、(11年广东-文15)如图4,在梯形ABCD中,AB∥CD,AB=4,CD=2,E、F分别为AD、BC上点,且EF=3,EF∥AB,则梯形ABFE与梯形EFCD的面积比为_______.
3、(2007湛江一模理)如图,在△ABC中,D是AC的中点,E是BD的中点,AE交BC于F,则 _____.17:51:21、三角形相似的判断方法;
2、解决问题的思维总结
1)抓住平行这一关键,构造相似(全等)三角形(或比例关系);
2)(乘积→)比例关系→相似(全等)三角形(或平行)。
3)线段长→三角形→相似(全等)三角形(相似三角形→比例关系→线段长)。教学内容(五)知识总结 布置作业讨论作业:P9,2;P10,4
要求:小组讨论,理清思路,代表“说题”作业:P19,7;P20,10弹性作业:
复习指导P154 17.1几何证明选讲(一)
及有关性质教学
目标1.通过自学与交流,理解平行线等分线段定理、平行线分线段成比例定理、相似三角形的判定及有关性质及直角三角形的射影定理
2.数形结合理解平行线等分线段定理、平行线分线段成比例定理、相似三角形的判定及有关性质及直角三角形的射影定理的用途、用法,会用它们解决一些简单问题。重点
难点重点:探究、理解定理、性质,会用它们解决一些简单问题;
难点:会用定理、性质解决一些简单问题;教学内容(一)预习交流,探究总结也相等平分第三边平分另一腰教学内容(一)预习交流,探究总结对应线段成比例教学内容(一)预习交流,探究总结相等成比例相似比或相似系数两角对应相等,两三角形相似两边对应成比例且夹角相等,
两三角形相似三边对应成比例,两三角形
相似对于直角三角形呢?教学内容(一)预习交流,探究总结两直角边在斜边上的射影射影斜边教学内容(二)说题解题 巩固知识【例1】如图,在ABCD中,M、N分别是AB、CD的中点,CM、AM分别交BD于E、F。求证:BE = EF = FD. t你认为求解的关键是什么?求解的关键是证明AN//MC.教学内容(二)说题解题 巩固知识【例2】△ABC中,DE∥BC,F是BC上一点。AF交DE于点G,
AD:BD=2:1,BC=8.4cm。求(1)DE的长;(2) ;(3) . t你认为求解的关键是什么?求解的关键是利用平行DE//BC.教学内容(二)说题解题 巩固知识【例3】已知:如图,△ABC 的高AD、BE交于点F.求证:
(1)AD?BC=BE?AC;(2)AF?FD=BF?FE. t你认为求解的关键是什么?求解的关键是乘积关系→比例
关系→相似三角形.教学内容(二)说题解题 巩固知识【例4】如图,圆内接△ABC的角平分线CD延长后交圆于一点E.求证:EB?CB=CE?BD.t在圆中求解问题注意利用“等弧对等角”求解的关键是乘积关系→比例
关系→相似三角形.教学内容(二)说题解题 巩固知识【例5】如图,在△ABC内任取一点D,连接AD和BD.点E在△ABC外,∠EBC=∠ABD,∠ECB=∠DAB.求证: △DBE∽△ABC.t已知与所求要相互结合分析解题思路题后小结 知能提升1、抓住平行这一关键,构造相似(全等)三角形(或比例关系);
2、(乘积→)比例关系→相似(全等)三角形(或平行)。
3、线段长→三角形→相似(全等)三角形(相似三角形→比例关系→线段长)。1、如图,在△ABC中,D是AB的中点,DE//BC交AC于E,EF//AB交BC于F。
(1)求证:BF=CF;
(2)图中与DE相等的线段有________;
(3)图中与EF相等的线段有_________;
(4)若连结DF,则DF与AC的位置关系是_______,数量关系是_______. 教学内容(三)跟进练习 强化知识2、如图:⊿APM中,AM∥BN,CM∥DN,
求证:PA:PB=PC:PD. 教学内容(三)跟进练习 强化知识3、已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC?BC=BE?CD;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.教学内容(四)高考模拟 身临其境1、(2008梅州一模文)如图,在四边形ABCD中,E为AB中点,EF//BC,FG//AD,则 _____.
2、(11年广东-文15)如图4,在梯形ABCD中,AB∥CD,AB=4,CD=2,E、F分别为AD、BC上点,且EF=3,EF∥AB,则梯形ABFE与梯形EFCD的面积比为_______.
3、(2007湛江一模理)如图,在△ABC中,D是AC的中点,E是BD的中点,AE交BC于F,则 _____.17:51:21、三角形相似的判断方法;
2、解决问题的思维总结
1)抓住平行这一关键,构造相似(全等)三角形(或比例关系);
2)(乘积→)比例关系→相似(全等)三角形(或平行)。
3)线段长→三角形→相似(全等)三角形(相似三角形→比例关系→线段长)。教学内容(五)知识总结 布置作业讨论作业:P9,2;P10,4
要求:小组讨论,理清思路,代表“说题”作业:P19,7;P20,10弹性作业:
复习指导P154 17.1几何证明选讲(一)
