人教版必修二第三单元直线与方程复习课件(27张)
文档属性
| 名称 | 人教版必修二第三单元直线与方程复习课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 353.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:49:59 | ||
图片预览






文档简介
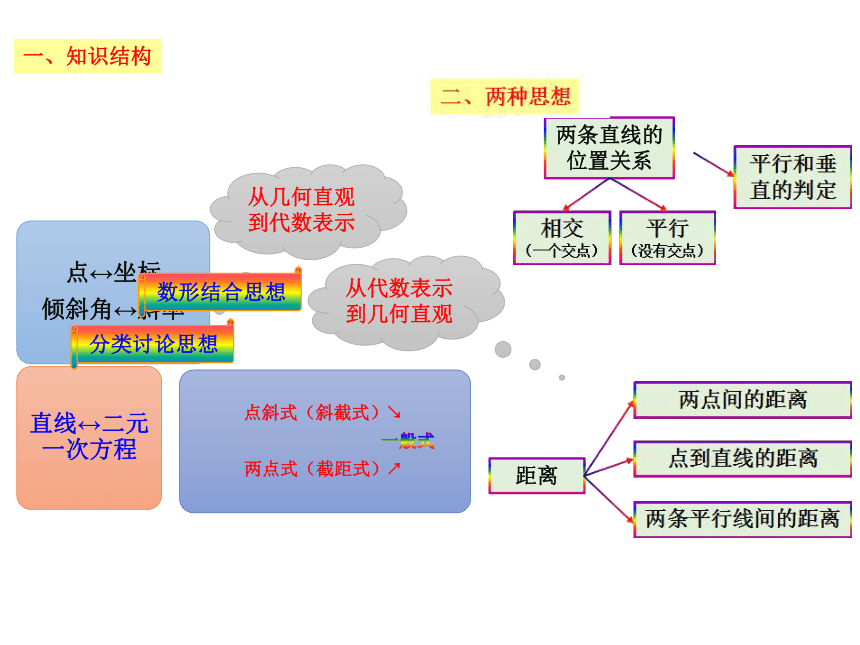
课件27张PPT。第三章 直线与方程复习 一、知识结构从几何直观到代数表示两条直线的位置关系距离从代数表示到几何直观数形结合思想分类讨论思想知识梳理1.直线的倾斜角:(1) 定义:
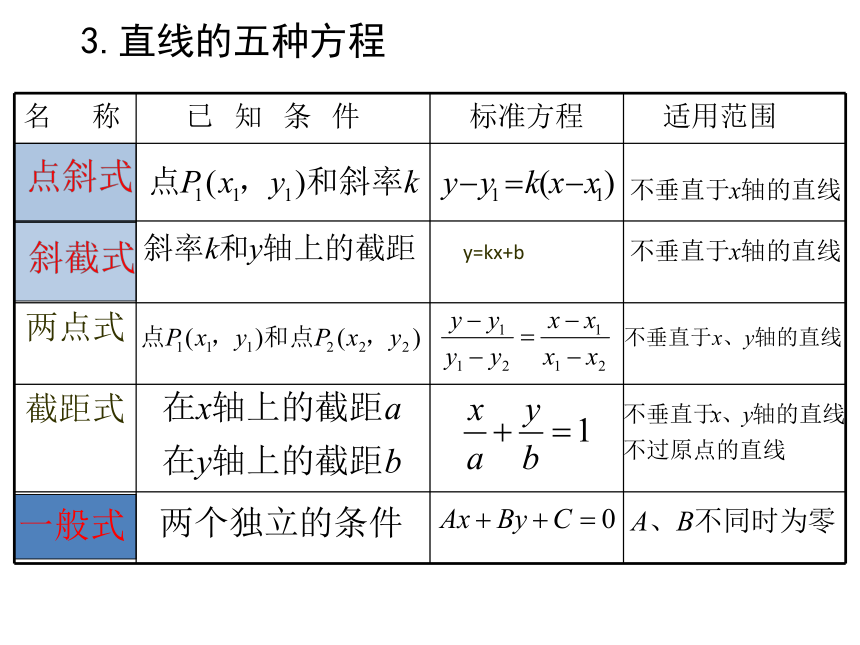
(2)范围: 2.直线的斜率:注意:与x轴垂直的直线不存在斜率 [0,π) 3.直线的五种方程 y=kx+b 关于直线的截距若直线l与x轴,y轴的交点分别为A(a,0),B(0,b),我们把坐标值a,b分别叫做x轴上的截距,y轴上的截距,或者横截距,纵截距,截距可正可负,亦可以为0.
4.两直线的位置关系 K1=K2且b1≠b2
K1=K2且b1=b2
K1≠K2
K1k2=-1
A1A2+B1B2=0
A1B2-A2B1=0且A1C2-A2C1≠0
(或B1C2-B2C1≠0) A1B2-A2B1=0且A1C2-A2C1=0
(或B1C2-B2C1=0) A1B2-A2B1≠0 (1)两点距离公式(3)两平行线间距离:l1:Ax+By+C1=0,l2:Ax+By+C2=05.三种距离(2)点到直线的距离公式
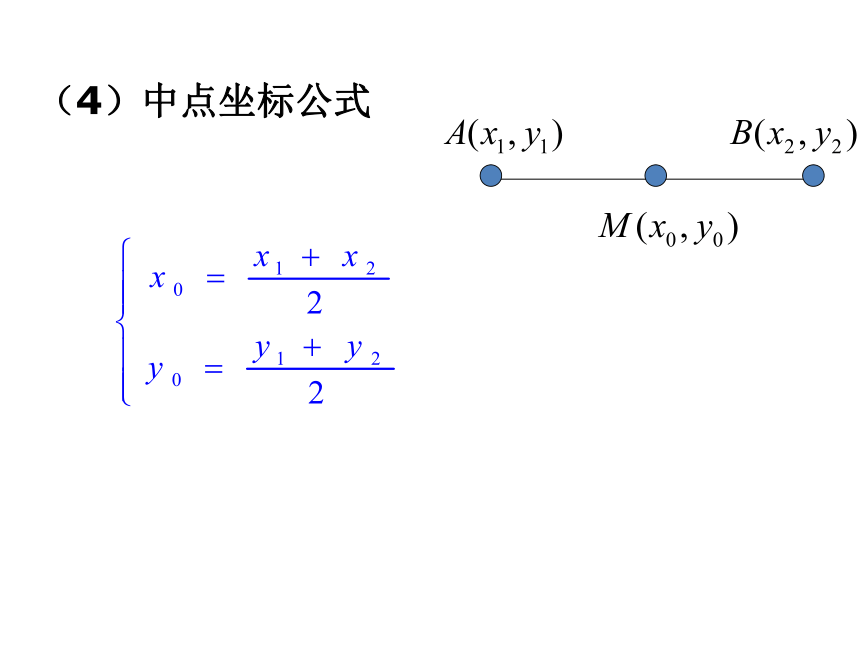
设点P(x0,y0),直线Ax+By+C=0,点A(x,y)到原点的距离(4)中点坐标公式 例1. 已知A(1,1),B(2,2),C(3,-1).
(1)求直线AB、AC的斜率和倾斜角;
(2)若D为△ABC的边BC上一动点,求直线AD的斜率k的取值范围. 分析:利用数形结合的方法,观察直线AD的变化情况,从而确定k的取值范围. 方法规律:
1.数形结合的方法既可以定性地分析倾斜角和斜率的
关系,也可以定量地求解倾斜角和斜率的取值范围.
2. 倾斜角与斜率的联系
(1)每一条直线都有倾斜角,但不一定有斜率,直线的倾斜角α
的范围是0°≤α<180°.
(2)当α=90°时,直线l垂直于x轴,它的斜率k不存在.
3.过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式:
例2.求与直线3x+4y+1=0平行,且在两坐标轴上截距之和为 的直线l的方程.
令x=0得y轴上的截距 令y=0得x轴上的截距 所以 解得m= -4, 所以所求直线l的方程为3x+4y-4=0.
解:方法一:设直线l的方程为3x+4y+m=0, 方法二:易知直线l在两坐标轴上的截距不为0,设直线l的方
程为
所以 解得
所以所求直线的方程为 即3x+4y-4=0.方法规律:1.直线方程的几种形式及确定
(1)直线方程的点斜式、斜截式、两点式、截距式都有各自的限制条件,不能表示所有的直线,直线方程的一般式则可以表示所有直线.
(2)在解题的时候,如果没有特别说明,最后的结果都要化成一般式.
2.确定直线方程的两种方法
(1)待定系数法,在设直线方程的时候,要注意对斜率不存在的直线讨论.
(2)从直线的几何性质出发,建立方程.
例3.已知直线l1:mx+8y+n=0,l2:2x+my-1=0,分别满足下列情况:(1)两直线平行.(2)两直线垂直,且l1在y轴上的截距为-1.试分别确定m,n的值.
解:(1)①当m=0时,显然l1不平行于l2. ②当m≠0时,l1,l2斜率都存在, 因为l1∥l2,故 所以m=±4. 又当m=4,n=-2时,两直线重合,当m=-4,n=2时,两直线重合, 所以当m=4,n≠-2或m=-4,n≠2时,两直线平行. (2)当2×m+m×8=0时,两直线垂直,即m=0, 方法规律:
1.两直线平行
(1)斜率存在且不重合的两条直线
l1:y=k1x+b1,l2:y=k2x+b2,则l1∥l2?k1=k2,b1≠b2.
(2)两条不重合直线l1,l2的倾斜角为α1,α2,则l1∥l2?α1=α2.
(3)两直线l1:A1x+B1y+C1=0(A1,B1,C1不同时为0),
l2:A2x+B2y+C2=0(A2,B2,C2不同时为0),则l1∥l2?A1B2-A2B1=0且A1C2-A2C1≠0(或B1C2-B2C1≠0).2.两直线垂直
(1)斜率存在的两条直线l1:y=k1x+b1,l2:y=k2x+b2,
则l1⊥l2?k1·k2=-1.
(2)两直线l1:A1x+B1y+C1=0(A1,B1,C1不同时为0),
l2:A2x+B2y+C2=0(A2,B2,C2不同时为0),则l1⊥l2?A1A2+B1B2=0.例4.直线经过点(3,4),且原点到它的距离为3,求该直线的方程。解:当直线的斜率存在时,设方程为y-4=k(x-3),即kx-y+4-3k=0
方程为当直线的斜率不存在时,方程为x=3,也符合题意 方法规律:
1.点到直线的距离公式
已知一点P(x0,y0)及一条直线l:Ax+By+C=0,则点P到直线l的
距离
2.两平行直线之间的距离
已知两平行直线l1:Ax+By+C1=0,l2:Ax+By+C2=0,则l1与l2之间
的距离
提醒:在应用此公式时,应将两条直线方程中x,y的系数化成
对应相同的形式.例6.求证:无论m取何实数时,直线(m-1)x-(m+3)y-(m-11)=0恒过定点,并求出定点的坐标.
解:即:故直线恒过点分别令m=1,m=-3,得到两个直线的方程,将其联立方法规律: 当m=1,n=0时,方程即为直线l1的方程;
当m=0,n=1时,方程即为直线l2的方程.
上面的直线系方程可改写为
(A1x+B1y+C1)+λ(A2x+B2y+C2)=0(其中λ∈R),但是方程中不包括直线l2,这个参数方程形式在解题中较为常用. 1.直线 x-y+1=0的倾斜角等于( )
A. B. C. D.
课堂练习
B 2.已知直线3x+4y-3=0与直线6x+my+14=0平行,则它们之间的距离是( )
A.1 B.2 C. D.4
【解析】因为直线3x+4y-3=0与直线6x+my+14=0平行,
所以,所以m=8,直线方程6x+my+14=0变为3x+4y+7=0
,则它们之间的距离是,所以选B。 B 3.已知直线l1:ax+2y+6=0,直线l2:x+(a-1)y+a2-1=0,
当l1∥l2时,a= ;当l1⊥l2时,a= .? 【解析】当l1∥l2时, ,解得 ;
当l1⊥l2时, ,解得 -1 4.点P(-1,2)到直线2x+y-10=0的距离为________。 5.求通过点(-1,2),且与直线y=2x+1平行的直线方程. 【解析】设与直线y=2x+1平行的直线方程为y=2x+b,因为直
线通过点(-1,2),所以2=2*(-1)+b,所以b=4,所以直线方
程为y=2x+4. 小结:1.直线的倾斜角的范围
斜率公式 ;
2.确定直线方程的方法:
3.直线的平行与垂直;
4.距离公式: ;
5.对称问题。 [0,π) 待定系数法
(2)范围: 2.直线的斜率:注意:与x轴垂直的直线不存在斜率 [0,π) 3.直线的五种方程 y=kx+b 关于直线的截距若直线l与x轴,y轴的交点分别为A(a,0),B(0,b),我们把坐标值a,b分别叫做x轴上的截距,y轴上的截距,或者横截距,纵截距,截距可正可负,亦可以为0.
4.两直线的位置关系 K1=K2且b1≠b2
K1=K2且b1=b2
K1≠K2
K1k2=-1
A1A2+B1B2=0
A1B2-A2B1=0且A1C2-A2C1≠0
(或B1C2-B2C1≠0) A1B2-A2B1=0且A1C2-A2C1=0
(或B1C2-B2C1=0) A1B2-A2B1≠0 (1)两点距离公式(3)两平行线间距离:l1:Ax+By+C1=0,l2:Ax+By+C2=05.三种距离(2)点到直线的距离公式
设点P(x0,y0),直线Ax+By+C=0,点A(x,y)到原点的距离(4)中点坐标公式 例1. 已知A(1,1),B(2,2),C(3,-1).
(1)求直线AB、AC的斜率和倾斜角;
(2)若D为△ABC的边BC上一动点,求直线AD的斜率k的取值范围. 分析:利用数形结合的方法,观察直线AD的变化情况,从而确定k的取值范围. 方法规律:
1.数形结合的方法既可以定性地分析倾斜角和斜率的
关系,也可以定量地求解倾斜角和斜率的取值范围.
2. 倾斜角与斜率的联系
(1)每一条直线都有倾斜角,但不一定有斜率,直线的倾斜角α
的范围是0°≤α<180°.
(2)当α=90°时,直线l垂直于x轴,它的斜率k不存在.
3.过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式:
例2.求与直线3x+4y+1=0平行,且在两坐标轴上截距之和为 的直线l的方程.
令x=0得y轴上的截距 令y=0得x轴上的截距 所以 解得m= -4, 所以所求直线l的方程为3x+4y-4=0.
解:方法一:设直线l的方程为3x+4y+m=0, 方法二:易知直线l在两坐标轴上的截距不为0,设直线l的方
程为
所以 解得
所以所求直线的方程为 即3x+4y-4=0.方法规律:1.直线方程的几种形式及确定
(1)直线方程的点斜式、斜截式、两点式、截距式都有各自的限制条件,不能表示所有的直线,直线方程的一般式则可以表示所有直线.
(2)在解题的时候,如果没有特别说明,最后的结果都要化成一般式.
2.确定直线方程的两种方法
(1)待定系数法,在设直线方程的时候,要注意对斜率不存在的直线讨论.
(2)从直线的几何性质出发,建立方程.
例3.已知直线l1:mx+8y+n=0,l2:2x+my-1=0,分别满足下列情况:(1)两直线平行.(2)两直线垂直,且l1在y轴上的截距为-1.试分别确定m,n的值.
解:(1)①当m=0时,显然l1不平行于l2. ②当m≠0时,l1,l2斜率都存在, 因为l1∥l2,故 所以m=±4. 又当m=4,n=-2时,两直线重合,当m=-4,n=2时,两直线重合, 所以当m=4,n≠-2或m=-4,n≠2时,两直线平行. (2)当2×m+m×8=0时,两直线垂直,即m=0, 方法规律:
1.两直线平行
(1)斜率存在且不重合的两条直线
l1:y=k1x+b1,l2:y=k2x+b2,则l1∥l2?k1=k2,b1≠b2.
(2)两条不重合直线l1,l2的倾斜角为α1,α2,则l1∥l2?α1=α2.
(3)两直线l1:A1x+B1y+C1=0(A1,B1,C1不同时为0),
l2:A2x+B2y+C2=0(A2,B2,C2不同时为0),则l1∥l2?A1B2-A2B1=0且A1C2-A2C1≠0(或B1C2-B2C1≠0).2.两直线垂直
(1)斜率存在的两条直线l1:y=k1x+b1,l2:y=k2x+b2,
则l1⊥l2?k1·k2=-1.
(2)两直线l1:A1x+B1y+C1=0(A1,B1,C1不同时为0),
l2:A2x+B2y+C2=0(A2,B2,C2不同时为0),则l1⊥l2?A1A2+B1B2=0.例4.直线经过点(3,4),且原点到它的距离为3,求该直线的方程。解:当直线的斜率存在时,设方程为y-4=k(x-3),即kx-y+4-3k=0
方程为当直线的斜率不存在时,方程为x=3,也符合题意 方法规律:
1.点到直线的距离公式
已知一点P(x0,y0)及一条直线l:Ax+By+C=0,则点P到直线l的
距离
2.两平行直线之间的距离
已知两平行直线l1:Ax+By+C1=0,l2:Ax+By+C2=0,则l1与l2之间
的距离
提醒:在应用此公式时,应将两条直线方程中x,y的系数化成
对应相同的形式.例6.求证:无论m取何实数时,直线(m-1)x-(m+3)y-(m-11)=0恒过定点,并求出定点的坐标.
解:即:故直线恒过点分别令m=1,m=-3,得到两个直线的方程,将其联立方法规律: 当m=1,n=0时,方程即为直线l1的方程;
当m=0,n=1时,方程即为直线l2的方程.
上面的直线系方程可改写为
(A1x+B1y+C1)+λ(A2x+B2y+C2)=0(其中λ∈R),但是方程中不包括直线l2,这个参数方程形式在解题中较为常用. 1.直线 x-y+1=0的倾斜角等于( )
A. B. C. D.
课堂练习
B 2.已知直线3x+4y-3=0与直线6x+my+14=0平行,则它们之间的距离是( )
A.1 B.2 C. D.4
【解析】因为直线3x+4y-3=0与直线6x+my+14=0平行,
所以,所以m=8,直线方程6x+my+14=0变为3x+4y+7=0
,则它们之间的距离是,所以选B。 B 3.已知直线l1:ax+2y+6=0,直线l2:x+(a-1)y+a2-1=0,
当l1∥l2时,a= ;当l1⊥l2时,a= .? 【解析】当l1∥l2时, ,解得 ;
当l1⊥l2时, ,解得 -1 4.点P(-1,2)到直线2x+y-10=0的距离为________。 5.求通过点(-1,2),且与直线y=2x+1平行的直线方程. 【解析】设与直线y=2x+1平行的直线方程为y=2x+b,因为直
线通过点(-1,2),所以2=2*(-1)+b,所以b=4,所以直线方
程为y=2x+4. 小结:1.直线的倾斜角的范围
斜率公式 ;
2.确定直线方程的方法:
3.直线的平行与垂直;
4.距离公式: ;
5.对称问题。 [0,π) 待定系数法
