人教版必修二3.1.1倾斜角与斜率课件(19张)
文档属性
| 名称 | 人教版必修二3.1.1倾斜角与斜率课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 510.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:51:44 | ||
图片预览

文档简介
课件19张PPT。3.1.1倾斜角与斜率学习目标: 1、理解直线的倾斜角和斜率的概念;
2、掌握过两点的直线的斜率公式;
3、通过坐标法的引入,培养学生联系、对应转化等辩证思维。1.一条直线的位置由哪些条件确定呢? 2.一点能否确定一条直线的位置吗?答:两点确定一条直线。 思考:一、直线的倾斜角:1、定义: 当直线l与x轴相交时,
我们取x轴作为基准,x轴
正向与直线l向上方向之间
所成的角 叫做直线的
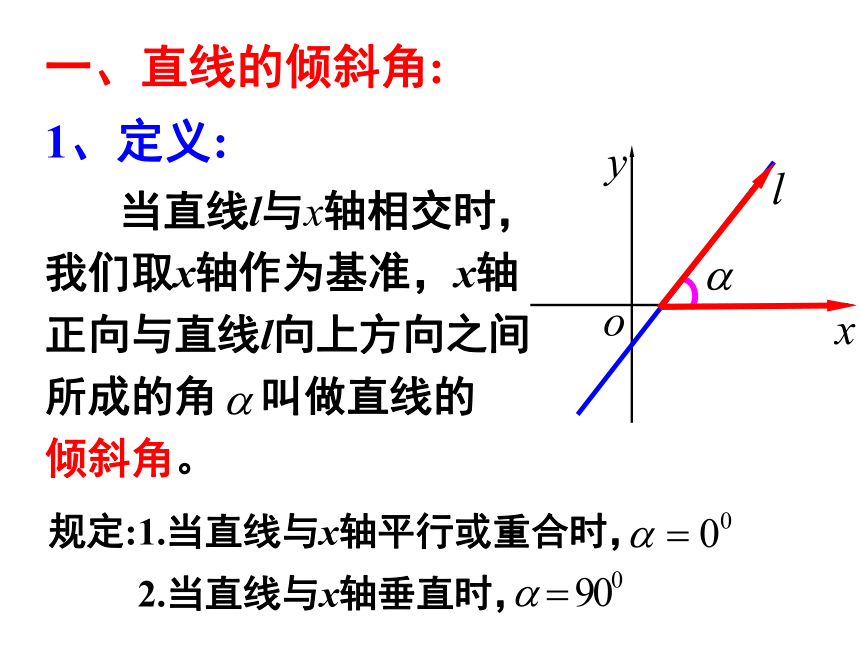
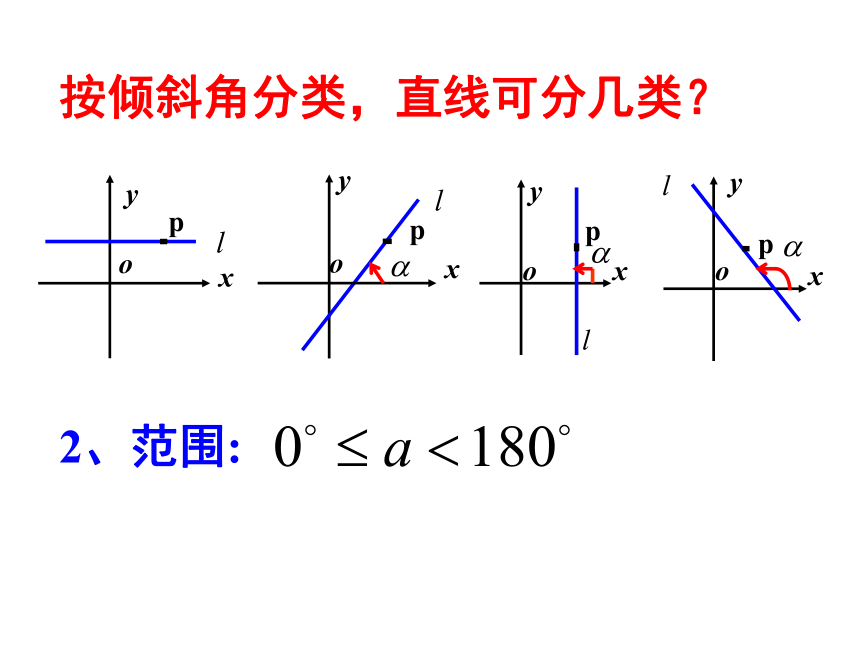
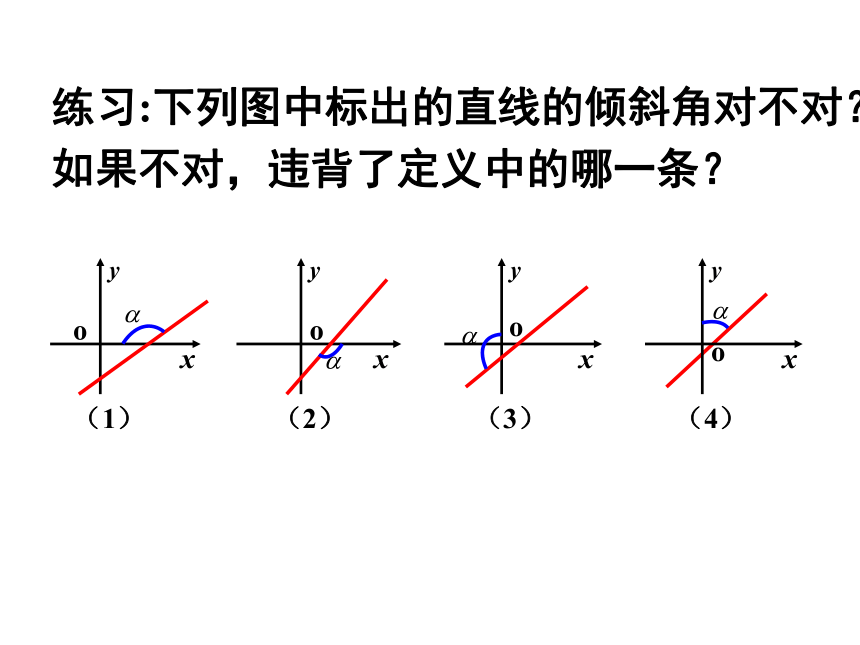
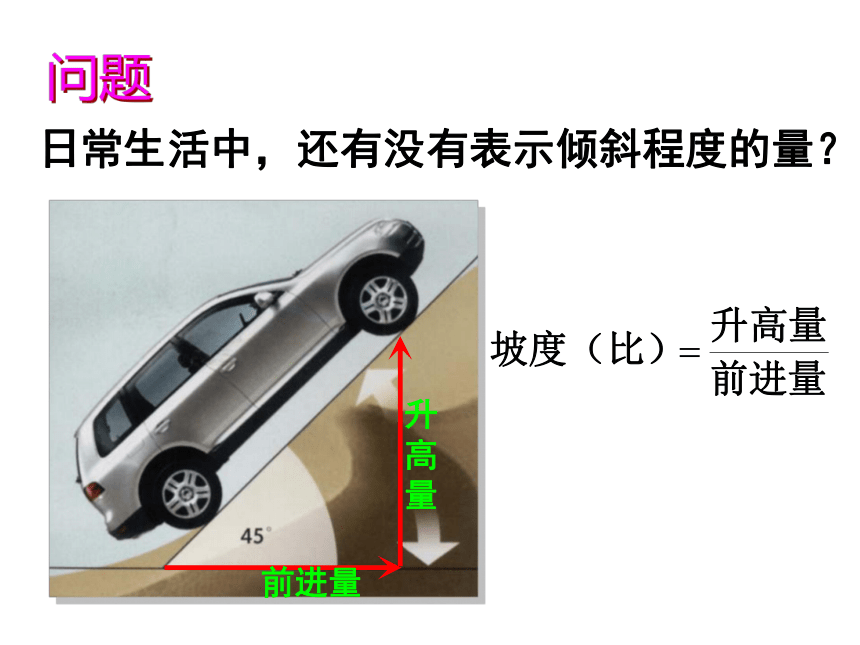
倾斜角。规定:1.当直线与x轴平行或重合时,2.当直线与x轴垂直时,按倾斜角分类,直线可分几类? 2、范围:练习:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?日常生活中,还有没有表示倾斜程度的量?问题升高量前进量A B C 设直线的倾斜程度为k 二、直线的斜率:1、定义:我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
用小写字母 k 表示,即: 是否每条直线都有斜率?2.如果倾斜角是锐角?3.如果倾斜角是直角?4.如果倾斜角是钝角?1.如果倾斜角是零度角?思考:练习:已知直线的倾斜角,求直线的斜率:
能不能构造一个直角三角形去求?由两点确定的直线的斜率:当α为锐角时, 倾斜角是锐角时 探究:当α为钝角时, 倾斜角是钝角时 1.当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?答:成立,因为分子为0,分母不为0,
k =0 思考:2.当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?答:斜率不存在,
因为分母为0。思考:三、直线的斜率公式:例1:如图,已知A(4,2)、B(-8,2)、C(0,-2),
求直线AB、BC、CA的斜率,并判断这些直线的倾斜角是什么角?∴直线CA的倾斜角为锐角∴直线BC的倾斜角为钝角解: ∴直线AB的倾斜角为零练习:解:【总一总★成竹在胸】核心知识?方法?思想直线的斜率下课
2、掌握过两点的直线的斜率公式;
3、通过坐标法的引入,培养学生联系、对应转化等辩证思维。1.一条直线的位置由哪些条件确定呢? 2.一点能否确定一条直线的位置吗?答:两点确定一条直线。 思考:一、直线的倾斜角:1、定义: 当直线l与x轴相交时,
我们取x轴作为基准,x轴
正向与直线l向上方向之间
所成的角 叫做直线的
倾斜角。规定:1.当直线与x轴平行或重合时,2.当直线与x轴垂直时,按倾斜角分类,直线可分几类? 2、范围:练习:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?日常生活中,还有没有表示倾斜程度的量?问题升高量前进量A B C 设直线的倾斜程度为k 二、直线的斜率:1、定义:我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
用小写字母 k 表示,即: 是否每条直线都有斜率?2.如果倾斜角是锐角?3.如果倾斜角是直角?4.如果倾斜角是钝角?1.如果倾斜角是零度角?思考:练习:已知直线的倾斜角,求直线的斜率:
能不能构造一个直角三角形去求?由两点确定的直线的斜率:当α为锐角时, 倾斜角是锐角时 探究:当α为钝角时, 倾斜角是钝角时 1.当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?答:成立,因为分子为0,分母不为0,
k =0 思考:2.当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?答:斜率不存在,
因为分母为0。思考:三、直线的斜率公式:例1:如图,已知A(4,2)、B(-8,2)、C(0,-2),
求直线AB、BC、CA的斜率,并判断这些直线的倾斜角是什么角?∴直线CA的倾斜角为锐角∴直线BC的倾斜角为钝角解: ∴直线AB的倾斜角为零练习:解:【总一总★成竹在胸】核心知识?方法?思想直线的斜率下课
