人教版必修二3.2.2直线的两点式方程课件(18张)
文档属性
| 名称 | 人教版必修二3.2.2直线的两点式方程课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 490.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 00:00:00 | ||
图片预览






文档简介
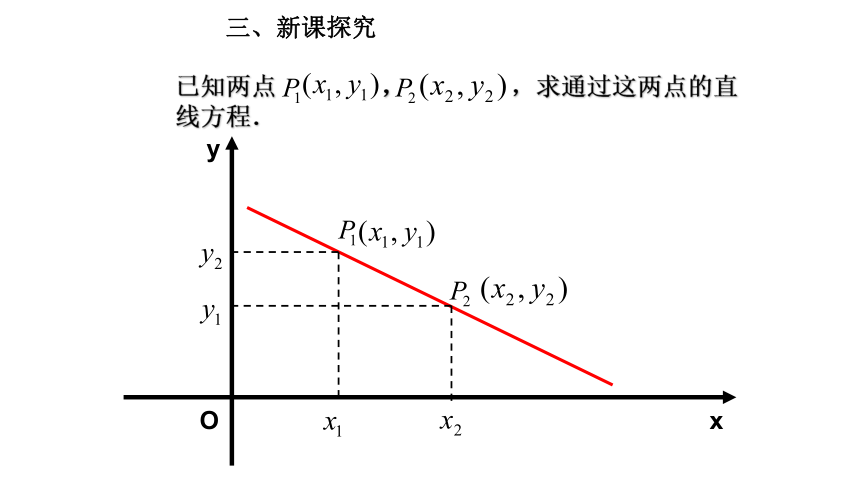
课件18张PPT。3.2.2 直线的两点式方程第三章 直线与方程 y=kx+b y- y0 =k(x- x0 )k为斜率, P0(x0 ,y0)为直线上的一定点 k为斜率,b为截距1). 直线的点斜式方程:2). 直线的斜截式方程: 一、复习回顾 Oxy已知两点 , ,求通过这两点的直线方程.三、新课探究(一)直线的两点式方程 经过两点P1(x1,y1), P2(x2,y2)(其中x1≠x2, y1≠y2 )的直线方程,叫做直线的两点式方程,简称两点式。记忆特点:1.左边全为y,右边全为x2.两边的分母全为常数 3.分子,分母中的减数相同两点式方程的形式上有什么特点?新课探究(一)直线的两点式方程(1)两点式方程的限制条件是 这个限制导致了哪些直线不能用两点式表示?不能表示与坐标轴(x,y轴)垂直的直线.练习 1.求过两点的直线的两点式方程已知两点坐标,求直线方程的方法:
①用两点式
②先求出斜率k,再用斜截式或点斜式。
③待定系数法 例1:已知直线 l 与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程.解:将两点A(a,0), B(0,b)的坐标代入两点式, 得:(二)直线的截距式方程注:直线与 x 轴的交点(a, 0)的横坐标 a 叫做直线在
x 轴上的截距; 直线与 y 轴的交点(0, b)的纵坐标 b 叫做直线在
y轴上的截距. 方程由直线在x轴和y轴上的截距确定,所以叫做直线方程的截距式方程;简称截距式(二)直线的截距式方程注意:等式的右边是常数1,
左边x项分母对应的是横截距a,
y项分母对应的是纵截距b,
中间以“+”连接!(二)直线的截距式方程②优点:注意:①局限性:(更大)是不是任意一条直线都有其截距式方程呢?不能表示过原点或与坐标轴垂直的直线由方程可直接得到直线与x,y轴的交点!?例2 三角形的顶点是A(-5,0),B(3,-3),C(0,2),求BC边
所在直线的方程,以及该边上中线所在直线的方程.解:过B(3,-3),C(0,2)两点式方程为:这就是BC边所在直线的方程.例3 求经过点P(-5,4),且在两坐标轴上的截距相等的
直线方程.分析:截距均为0时,设方程为y=kx,
截距不为0,设截距式求解.解:当截距均为0时,设方程为y=kx,
把P(-5,4)代入上式得
即直线方程为
当截距均不为0时,设直线方程为
把P(-5,4)代入上式得
直线方程为
即
综上直线方程为 或达标检测
①用两点式
②先求出斜率k,再用斜截式或点斜式。
③待定系数法 例1:已知直线 l 与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程.解:将两点A(a,0), B(0,b)的坐标代入两点式, 得:(二)直线的截距式方程注:直线与 x 轴的交点(a, 0)的横坐标 a 叫做直线在
x 轴上的截距; 直线与 y 轴的交点(0, b)的纵坐标 b 叫做直线在
y轴上的截距. 方程由直线在x轴和y轴上的截距确定,所以叫做直线方程的截距式方程;简称截距式(二)直线的截距式方程注意:等式的右边是常数1,
左边x项分母对应的是横截距a,
y项分母对应的是纵截距b,
中间以“+”连接!(二)直线的截距式方程②优点:注意:①局限性:(更大)是不是任意一条直线都有其截距式方程呢?不能表示过原点或与坐标轴垂直的直线由方程可直接得到直线与x,y轴的交点!?例2 三角形的顶点是A(-5,0),B(3,-3),C(0,2),求BC边
所在直线的方程,以及该边上中线所在直线的方程.解:过B(3,-3),C(0,2)两点式方程为:这就是BC边所在直线的方程.例3 求经过点P(-5,4),且在两坐标轴上的截距相等的
直线方程.分析:截距均为0时,设方程为y=kx,
截距不为0,设截距式求解.解:当截距均为0时,设方程为y=kx,
把P(-5,4)代入上式得
即直线方程为
当截距均不为0时,设直线方程为
把P(-5,4)代入上式得
直线方程为
即
综上直线方程为 或达标检测
