人教版必修二第三单元直线的方程复习课课件(45张)
文档属性
| 名称 | 人教版必修二第三单元直线的方程复习课课件(45张) |  | |
| 格式 | zip | ||
| 文件大小 | 455.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:55:16 | ||
图片预览











文档简介
课件45张PPT。3.2 直线的方程
教学目标:
1.理解直线方程的点斜式、斜截式、两点式、截距式的形式特点和适用范围;
2.明确直线方程一般式的形式特征;
3.能正确利用直线的点斜式、斜截式、两点式、截距式公式求直线方程;
4.体会直线的斜截式方程与一次函数的关系;
5.会把直线方程的一般式化为斜截式,进而求斜率和截距;
6.会把直线方程的点斜式、两点式化为一般式.(一)直线方程点斜式
如图:直线l过定点P0(x0,y0)且斜率为k,那么l上任一点P(x,y)的坐标满足什么关系?通过这一关系进一步说明了什么?提示:由斜率公式得k= 即y-y0=k(x-x0).并且过
点P0(x0,y0)斜率为k的直线l上每一点的坐标都满足
该关系;坐标满足该关系的每一点都在过点P0(x0,y0), 斜率为k的直线l上.结论:直线的点斜式方程方程___ _________由直线上一定点(x0,y0)及其斜率
k确定,我们把这个方程叫直线的点斜式方程,简称点斜式.y-y0=k(x-x0)例1.(1)经过点(4,-1)且平行于x轴的直线方程为__________.?
(2)已知在△ABC中,A(1,-4),B(2,6),C(-2,0),AD⊥BC于点D,求直线AD的方程.【解析】(1)因为所求直线平行于x轴,故斜率k=0,所以直线的方程为
y-(-1)=0(x-4),即y=-1.答案:y=-1(2)由题意知,kBC= .因为AD⊥BC,所以直线AD的斜率存在,且
kAD=- .故直线AD的方程为y+4=- (x-1).
变式训练1.已知在△ABC中,A(1,-1),B(2,2),C(3,0),则AB边上的高线所在直线方程为__________.?
【解析】kAB= =3,
所以AB边上的高线的斜率k=- ,
所以AB边上的高线的点斜式方程为y=- (x-3),
即x+3y-3=0.
答案:x+3y-3=0变式训练2.已知直线l经过点( ,-2),其倾斜角是60°.
(1)求直线l的方程.
(2)求直线l与两坐标轴围成三角形的面积.【解析】(1)因为k=tan 60°= ,
所以直线l的方程为y+2= (x- ),化为 x-y-5=0,
即为所求的直线l的方程.(2)令x=0,解得y=-5;令y=0,解得x= .
所以直线l与两坐标轴围成三角形的面积
课后作业:1.写出满足下列条件的直线的点斜式 方程: (1)经过点A(-3,-1),斜率为 . (2)经过点B( ,1),倾斜角是120°. (3)经过点C(0,5)且与x轴平行.【解析】(1)y+1= (x+3). (2)倾斜角为120°,则斜率为- ,所以该直线方程为y-1=- (x- ). (3)因为直线与x轴平行,故斜率为0,因此点斜式方程为y-5=0(x-0).2.过点P(2 ,3)且倾斜角为30°的直线方程为( )
A.y-4 =3x B.y=x-
C.3y-3= x D.y- = x【解析】选C.因为直线的倾斜角为30°,所以其斜率
为tan 30°= ,
因为直线过点(2 ,3),所以直线方程为y-3= (x-2 ),
即y= x+1, x-3y+3=0.(二)直线方程的斜截式
1.斜率为k,与y轴的交点为(0,b)的直线的点斜式方程是什么?
提示:由点斜式方程的特点知,斜率为k,过点(0,b)的直线点斜式方程为y-b=k(x-0).2.若把直线l与y轴交点的纵坐标b称为直线l在y轴上的截距,那么直线l的方程能否用该直线的斜率k与该直线在y轴上的截距b表示?
提示:可以,因为直线l过点(0,b)且斜率为k,故直线l的方程为y-b=k(x-0),化简得y=kx+b,因此直线l的方程可以用k,b表示.结论:截距与斜截式方程
直线l与y轴交点的纵坐标叫做直线l在y轴上的截距;由斜率和它在y轴上的截距确定的方程叫直线的斜截式方程.形式:y=kx+b.例1.倾斜角为135°,在y轴上的截距为-1的直线方程是 ( )
A.y=x+1 B.y=x-1 C.y=-x+1 D.y=-x-1【解析】选D.因为倾斜角为135°,所以k=tan 135°=-1.
所以直线方程为y=-x-1.变式训练1.已知直线l1:y=-ax-2(a∈R).若直线l1的倾斜角为120°,则实数a的值为_______;若直线l1在x轴上的截距为2,则实数a的值为_______.【解析】由题意可得tan 120°= -a,解得a= ;
令y=0,可得x= ,
即直线l1在x轴上的截距为 =2,解得a=-1.
答案: -1例2.若直线l的倾斜角为45°,且在y轴上的截距为1,则直线l的斜截式方程为____________.?
【解析】因为k=tan 45°=1,直线l在y轴上截距为1,故直线l的方程为y=x+1.
答案:y=x+1【解析】因为直线的方程为y=- x+1,所以k=- ,倾斜角为120°,
由题知所求直线的倾斜角为30°,即斜率为 .
因为所求直线在y轴上的截距为-5,
所以由斜截式知所求直线方程为y= x-5.变式训练2.求倾斜角是直线y=- x+1的倾斜角的 ,且满足在y轴上的截距是-5的直线方程.
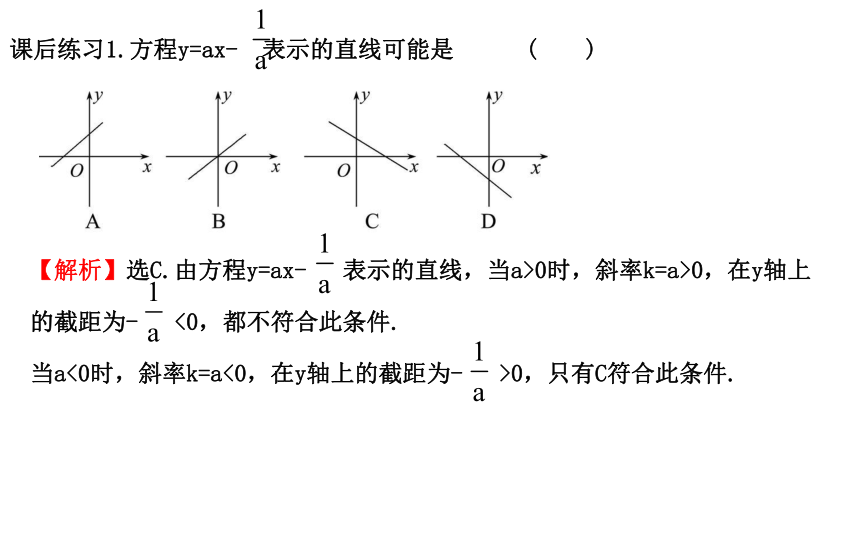
课后练习1.方程y=ax- 表示的直线可能是 ( )【解析】选C.由方程y=ax- 表示的直线,当a>0时,斜率k=a>0,在y轴上的截距为- <0,都不符合此条件.
当a<0时,斜率k=a<0,在y轴上的截距为- >0,只有C符合此条件.2.已知直线l的斜率为 ,且和两坐标轴围成的三角
形的面积为3,求直线l的方程.【解析】设l的方程为y= x+b,分别令x=0,y=0得y=b,x=-6b,
依题意有 ×|b|×|-6b|=3,所以b2=1,
解得b=±1,
所以l的方程为y= x+1或y= x-1.(三)两条直线的平行与垂直的应用
例1.已知直线l1:y=-x+2a与直线l2:y=(a2-2)x+2.
(1)当a为何值时,l1∥l2?(2)当a为何值时,l1⊥l2?【解析】设直线l1,l2斜率分别为k1,k2,
则k1=-1,k2=a2-2.
(1)当l1∥l2时,有 解得a=-1.
(2)当l1⊥l2时,k1k2=-1,即a2-2=1,
所以a2=3,所以a=
变式训练1.已知直线l1:x-my-6=0,l2:(m-2)x-3y-2m=0.若l1⊥l2,则m的值为__________.若l1∥l2,则m的值为__________.?【解析】由两直线垂直可得:1·(m-2)+m·3=0,解得m= ,
故当l1⊥l2时,m= ;由平行的条件可得:
由 解得m=-1或m=3;
而当m=3时,l1与l2重合,不满足题意,舍去,
故m=-1.
答案: ,-1例2.已知直线l1的方程为y=-2x+3.
(1)若直线l2与l1平行,且过点(-1,3),求直线l2的方程.
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.【解析】(1)由直线l2与l1平行,可设l2的方程为y=-2x+b,将x=-1,y=3代入,得3=(-2)×(-1)+b,即得b=1,
所以直线l2的方程为y=-2x+1.(2)由直线l2与l1垂直,可设l2的方程为y= x+m,
令y=0,得x=-2m,令x=0,得y=m,
故三角形面积S= |-2m|·|m|=4,
所以m2=4,解得m=±2,所以直线l2的方程是y= x+2或y= x-2.课后练习 1.当a为何值时,
(1)两直线y=(a+1)x-2与y=(a-1)x+1互相垂直?
(2)两直线y=-x+4a与y=(a2-2)x+4互相平行?【解析】(1)因为两直线y=(a+1)x-2与y=(a-1)x+1互相垂直,
所以(a+1)(a-1)=-1,即a=0.
(2)因为两直线y=-x+4a与y=(a2-2)x+4互相平行.
所以 即a=-1.(四)直线方程的两点式
观察如图所示的直线l,思考下列问题:
1.直线l经过点P1(x1,y1),P2(x2,y2)(其中x1≠x2)两点,那么直线l的点斜式方程是什么? 提示:由x1≠x2,所求直线的斜率为k= ,则直线的点斜式方程为y-y1= (x-x1).2.方程y-y1= (x-x1)(x1≠x2)能否写成
提示:当y1≠y2时,可以写成上式;当y1=y2时,不能
写成该形式.结论:两点式方程的形式_________ (x1≠x2,y1≠y2),当x1=x2时,方程
为_ ___,当y1=y2时,方程为__ __.x=x1y=y1例1.经过两点(x1,y1),(x2,y2)的直线方程都可以表示为( ) C.(y-y1)(x2-x1)=(x-x1)(y2-y1)
D.y-y1= 【解析】选C.当x1≠x2,y1≠y2时,由两点式可得直线方程为:
化为:(y-y1)(x2-x1)=(x-x1)(y2-y1),对于x1=x2或y1=y2时上述方程也成立,
因此直线方程为:(y-y1)(x2-x1)=(x-x1)(y2-y1).
变式训练1:过点A(2,3)和点B(4,7)的直线方程是( )
A.y=-2x+7 B.y=2x+1 C.y=2x-1 D.y=2
【解析】选C.直线的两点式方程为 即y=2x-1变式训练1.在△ABC中,已知点A(5,-2),B(7,3)且边AC的中点M在y轴上,边BC的中点N在x轴上.(1)求点C的坐标.(2)求直线MN的方程.【解析】(1)设C(x,y)得
因为M在y轴上,N在x轴上,所以 ,解得x=-5,y=-3.
所以C点坐标为(-5,-3).(2)由(1)知M ,N(1,0),
所以直线MN的方程为 例2.已知在平面直角坐标系中,△ABC三个顶点坐标分别为A(1,3),B(5,1),C(-1,-1).
(1)求BC边的中线AD所在的直线方程.(2)求AC边的高BH所在的直线方程.【解析】(1)BC中点D的坐标为(2,0),所以直线AD方程为: 化简得y=-3x+6.
(2)因为kAC= =2,BH⊥AC,所以kBH=- ,
所以直线BH方程为:y-1=- (x-5),即y=- x+ .变式训练2.△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0).
(1)求边AC和AB所在直线的方程.
(2)求边AC上的中线BD所在的直线的方程.【解析】(1)因为A(0,4),C(-8,0),所以直线AC的截距式方程为
化简得y= x+4,
因为B(-2,6),A(0,4),
所以由直线的两点式方程,得AB方程为
即y=-x+4.综上所述,边AC所在直线的方程为y= x+4,边AB所在直线的方程为y=-x+4.(2)设点D(x,y),由线段的中点坐标公式,可得
所以AC中点D的坐标为(-4,2),再由直线的两点式方程,得BD所在直线的方程为 化简得y=2x+10,即为所求边AC上的中线BD所在的直线的方程.(五)直线的截距式方程
1.若直线l经过点A(a,0)与点B(0,b),则直线l的两点式方程是什么?
提示:当a≠0且b≠0时,直线l的两点式方程为 2.问题1中的方程有何特点?
提示:直线l与x轴交点的横坐标a叫做直线在x轴上的截距,因此问题1中的方程是由直线在两个坐标轴上的截距确定的.结论:截距式方程的形式:______________________ .例1.若直线l的方程为 =1,则直线l在x轴与y轴
上的截距分别是 ( )
【解析】选B.直线的截距式方程中x的分母为直线在x轴上的截距,y的分母为直线在y轴上的截距.变式训练1:直线 (ab≠0)在y轴上的截距是 ( )
A.a B.b C.-a D.-b【解析】选D.直线 (ab≠0)中,
令x=0,解得y=-b,所以直线 在y轴上的截距为-b.变式训练2.直线l过点(-3,3),且在两坐标轴上的截距之和为12,求直线l的方程.【解析】由题意设直线l的方程为 则a+b=12, ①
又直线l过点(-3,3),所以 ②
联立①②解得
故所求的直线方程为 例2.在x轴、y轴上的截距分别是2,-3的直线方程为( )【解析】选B.在x轴,y轴上的截距分别是2,-3的直线的方程是 变式训练2:过定点(2,3)且在两坐标轴上截距的绝对值相等的直线有n条,则n的值为 ( )
A.1 B.2 C.3 D.以上答案都不对【解析】选C.①若此直线经过原点,则斜率k= ,所以要求的直线方程为3x-2y=0;②当直线不经过原点时,由题意是直线的方程为x±y=a,把(2,3)代入上述直线的方程得2±3=a,解得a=5或-1.所以直线的方程为x+y-5=0,x-y+1=0.
课后练习 1.过点P(-2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形面积为8,这样的直线l一共有 ( )
A.3条 B.2条 C.1条 D.0条【解析】选C.假设存在过点P(-2,2)的直线l,使它与两坐标轴围成的三角形的面积为8,设直线l的方程为: (a<0,b>0),则 即2a-2b=ab.
直线l与两坐标轴在第二象限内围成的三角形面积S=- ab=8,
即ab=-16,联立 解得:a=-4,b=4.
所以直线l的方程为: 即y=x+4,
即这样的直线有且只有一条.
(六)直线方程的一般式
1.平面直角坐标系中的每一条直线l都可以用一个关于x,y的二元一次方程表示吗?提示:可以,当直线l斜率k存在时,在直线l上任取一点P0(x0,y0),其方程为y-y0=k(x-x0),这是关于x,y的二元一次方程,当直线l斜率不存在,即直线l的倾斜角α=90°时,直线的方程为x-x0=0,这也是关于x,y的二元一次方程.2.每一个关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示一条直线
吗?提示:都表示.当B≠0时,方程可变形为y=
它表示过点 (0,- ),斜率为- 的直线,当B=0时,则x=- ,它表示过
(- ,0),垂直于x轴的一条直线,故每一个关于x,y的二元一次方程都表
示一条直线.结论:直线方程的一般式
我们把关于x,y的二元一次方程______________________________ 叫做直线的一般式方程,简称一般式.Ax+By+C=0(其中A,B不同时为0)例1.直线l的方程为Ax+By+C=0,若直线l过原点和第二、四象限,则( )
A.C=0,A>0 B.C=0,A>0,B>0 C.AB<0,C=0 D.AB>0,C=0【解析】 选D.因为直线l过原点,所以C=0.又因为l过第二、四象限,故- <0,所以AB>0.变式训练1:方程2x-3y-1=0在x轴上的截距为____________;在y轴上的截距为____________.?【解析】令x=0,得y=- ,令y=0,得x= ,所以直线在x轴、y轴上的截距分别为 ,- .
答案: - 例2.把直线l的方程2x-3y-6=0化成截距式,指出直线在x轴、y轴上的截距,并画出图形.
【解析】由2x-3y-6=0,得2x-3y=6,即
该直线在x轴、y轴上的截距分别为3与-2,画出图形如
图所示:
变式训练2:本例条件不变,试将直线l的方程化成斜截式并指出它的斜率与截距.
【解析】由2x-3y-6=0得3y=2x-6,
所以y= x-2,其中斜率为 ,截距为-2.
变式训练3.若把本例中的直线方程“2x-3y-6=0”换为“-4x+7y-28=0”,其结论又如何呢?【解析】由-4x+7y-28=0,得-4x+7y=28,即
其中在x轴,y轴上的截距分别为-7与4.
图形如图所示:例3:直线x-y-1=0的倾斜角与其在y轴上的截距分别是 ( )
A.135°,1 B.45°,-1 C.45°,1 D.135°,-1【解析】选B.根据题意,直线的方程为x-y-1=0,变形可得y=x-1,
则其斜率k=1,倾斜角为45°,在y轴上的截距为-1.变式训练4.直线2x-5y-10=0与坐标轴围成三角形的面积为( )
A.5 B.10 C.15 D.20
【解析】选A.直线2x-5y-10=0与坐标轴的交点坐标为(0,-2),(5,0),
所以直线2x-5y-10=0与坐标轴所围成的三角形面积是: ×2×5=5.课后练习 1.数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标是( )A.(-4,0) B.(0,-4) C.(4,0) D.(4,0)或(-4,0)【解析】选A.设C(m,n),由重心坐标公式得,
三角形ABC的重心为
代入欧拉线方程得:
整理得:m-n+4=0 ①AB的中点为(1,2),kAB= AB的中垂线方程为y-2= (x-1),
即x-2y+3=0.
联立 所以△ABC的外心为(-1,1).则(m+1)2+(n-1)2=32+12=10,整理得:m2+n2+2m-2n=8 ②联立①②得:m=-4,n=0或m=0,n=4,m=0,n=4时,B,C重合,舍去.所以顶点C的坐标是(-4,0).2.(1)如果直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0(a∈R)平行,那么a=_____.?
(2)已知直线l1:(k-3)x+(5-k)y+1=0与l2:2(k-3)x-2y+3=0垂直,则k的值是____.?【解析】(1)当a=0时,不符合题意;当a=-1时,不符合题意;
当a≠0且a≠-1时,l1可化为y= l2可化为y=
由题意知 解得a=-2或a=1.答案:-2或1
(2)由l1⊥l2,得2(k-3)2+(5-k)×(-2)=0,即k2-5k+4=0,解得k=1或k=4.
答案:1或4【总结】利用一般式直线方程判断直线位置关系的方法若直线l1:A1x+B1y+C1=0( ≠0),l2:A2x+B2y+C2=0( ≠0),则:
(1)当A1B2-A2B1≠0时,l1与l2相交.(2)当A1B2-A2B1=0且B1C2-B2C1≠0时,l1∥l2.
(3)当A1B2-A2B1=0且B1C2-B2C1=0时,l1与l2重合.
(4)当A1A2+B1B2=0时,l1⊥l2.3.直线mx+(2m-1)y+1=0和直线3x+my+3=0垂直,则实数m的值为_________.?【解析】本题主要考查两直线垂直关系.若两直线垂直,则有3m+(2m-1)m=0,
即m2+m=0,解得m=0或-1.答案:0或-14.已知三条直线l1:2x+my+2=0(m∈R):l2:2x+y+1=0,l3:x+ny+1=0(n∈R),若l1∥l2,l1⊥l3,则m+n的值为__________.?【解析】因为l1∥l2,所以 =-2,解得m=1.因为l1⊥l3,m=n=0不满足题意,舍去,所以 =-1,解得n=-2.
则m+n=-1.
答案:-1(七)直线方程的综合应用
例1.已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限.
(2)为使直线不经过第二象限,求a的取值范围.【解析】(1)将直线l的方程整理为 所以l的斜率为a,且过定点
而点 在第一象限,故l必过第一象限.(2)直线OA的斜率为 因为l不经过第二象限,
所以a≥3,故a的取值范围是[3,+∞).变式训练1.已知直线l1:2x-y+1=0和直线l2:x+y-4=0相交于点A,O是坐标原点,直线l3经过点A且与OA垂直.
(1)求直线l3的方程.
(2)若点B在直线l3上,且|OB|=10,求点B的坐标.【解析】(1) ?A(1,3),所以kOA=3,得直线l3的斜率是 ,
所以直线l3的方程:y-3= (x-1),即x+3y-10=0.(2)设B(10-3m,m),
由|OB|=10,得 得m=6或0,
所以B(10,0)或B(-8,6).例2.一条光线从点A(3,2)发出,经x轴反射,通过点B(-1,6),求入射光线和反射光线所在直线的方程.
【解析】点A关于x轴的对称点为A1(3,-2),点B关于x轴的对称
点为B1(-1,-6).
因为A1在反射光线的延长线上,B1在入射光线的延长线上,由两点式可得直线A1B的方程为 化简得2x+y-4=0;直线AB1的方程为
化简得2x-y-4=0.
所以入射光线所在直线方程为2x-y-4=0,
反射光线所在直线方程为2x+y-4=0.
变式训练2.已知有条光线从点A(-2,1)出发射向x轴点B,经过x轴反射后射向y轴上的C点,再经过y轴反射后到达点D(-2,7).求直线BC的方程.【解析】如图所示,因为A(-2,1),所以A点关于x轴的对称点为A′(-2,-1),因为D(-2,7),所以D点关于y轴的对称点D′(2,7).
由对称性可得,A′、D′所在直线方程即为BC所在
直线方程,所以直线BC的方程为
整理得2x-y+3=0.变式训练3.已知光线通过点A(2,3),经直线x+y+1=0反射,其反射光线通过点B(1,1),求入射光线和反射光线所在直线方程.【解析】求得点A(2,3)关于直线x+y+1=0的对称点A′(-4,-3).
则由两点式求得反射光线所在的直线A′B的方程为
由 求得直线A′B与直线x+y+1=0的交点
由两点式求得入射光线所在的直线AC的方程为
综上,入射光线所在直线方程为
反射光线所在直线方程为
谢谢!
教学目标:
1.理解直线方程的点斜式、斜截式、两点式、截距式的形式特点和适用范围;
2.明确直线方程一般式的形式特征;
3.能正确利用直线的点斜式、斜截式、两点式、截距式公式求直线方程;
4.体会直线的斜截式方程与一次函数的关系;
5.会把直线方程的一般式化为斜截式,进而求斜率和截距;
6.会把直线方程的点斜式、两点式化为一般式.(一)直线方程点斜式
如图:直线l过定点P0(x0,y0)且斜率为k,那么l上任一点P(x,y)的坐标满足什么关系?通过这一关系进一步说明了什么?提示:由斜率公式得k= 即y-y0=k(x-x0).并且过
点P0(x0,y0)斜率为k的直线l上每一点的坐标都满足
该关系;坐标满足该关系的每一点都在过点P0(x0,y0), 斜率为k的直线l上.结论:直线的点斜式方程方程___ _________由直线上一定点(x0,y0)及其斜率
k确定,我们把这个方程叫直线的点斜式方程,简称点斜式.y-y0=k(x-x0)例1.(1)经过点(4,-1)且平行于x轴的直线方程为__________.?
(2)已知在△ABC中,A(1,-4),B(2,6),C(-2,0),AD⊥BC于点D,求直线AD的方程.【解析】(1)因为所求直线平行于x轴,故斜率k=0,所以直线的方程为
y-(-1)=0(x-4),即y=-1.答案:y=-1(2)由题意知,kBC= .因为AD⊥BC,所以直线AD的斜率存在,且
kAD=- .故直线AD的方程为y+4=- (x-1).
变式训练1.已知在△ABC中,A(1,-1),B(2,2),C(3,0),则AB边上的高线所在直线方程为__________.?
【解析】kAB= =3,
所以AB边上的高线的斜率k=- ,
所以AB边上的高线的点斜式方程为y=- (x-3),
即x+3y-3=0.
答案:x+3y-3=0变式训练2.已知直线l经过点( ,-2),其倾斜角是60°.
(1)求直线l的方程.
(2)求直线l与两坐标轴围成三角形的面积.【解析】(1)因为k=tan 60°= ,
所以直线l的方程为y+2= (x- ),化为 x-y-5=0,
即为所求的直线l的方程.(2)令x=0,解得y=-5;令y=0,解得x= .
所以直线l与两坐标轴围成三角形的面积
课后作业:1.写出满足下列条件的直线的点斜式 方程: (1)经过点A(-3,-1),斜率为 . (2)经过点B( ,1),倾斜角是120°. (3)经过点C(0,5)且与x轴平行.【解析】(1)y+1= (x+3). (2)倾斜角为120°,则斜率为- ,所以该直线方程为y-1=- (x- ). (3)因为直线与x轴平行,故斜率为0,因此点斜式方程为y-5=0(x-0).2.过点P(2 ,3)且倾斜角为30°的直线方程为( )
A.y-4 =3x B.y=x-
C.3y-3= x D.y- = x【解析】选C.因为直线的倾斜角为30°,所以其斜率
为tan 30°= ,
因为直线过点(2 ,3),所以直线方程为y-3= (x-2 ),
即y= x+1, x-3y+3=0.(二)直线方程的斜截式
1.斜率为k,与y轴的交点为(0,b)的直线的点斜式方程是什么?
提示:由点斜式方程的特点知,斜率为k,过点(0,b)的直线点斜式方程为y-b=k(x-0).2.若把直线l与y轴交点的纵坐标b称为直线l在y轴上的截距,那么直线l的方程能否用该直线的斜率k与该直线在y轴上的截距b表示?
提示:可以,因为直线l过点(0,b)且斜率为k,故直线l的方程为y-b=k(x-0),化简得y=kx+b,因此直线l的方程可以用k,b表示.结论:截距与斜截式方程
直线l与y轴交点的纵坐标叫做直线l在y轴上的截距;由斜率和它在y轴上的截距确定的方程叫直线的斜截式方程.形式:y=kx+b.例1.倾斜角为135°,在y轴上的截距为-1的直线方程是 ( )
A.y=x+1 B.y=x-1 C.y=-x+1 D.y=-x-1【解析】选D.因为倾斜角为135°,所以k=tan 135°=-1.
所以直线方程为y=-x-1.变式训练1.已知直线l1:y=-ax-2(a∈R).若直线l1的倾斜角为120°,则实数a的值为_______;若直线l1在x轴上的截距为2,则实数a的值为_______.【解析】由题意可得tan 120°= -a,解得a= ;
令y=0,可得x= ,
即直线l1在x轴上的截距为 =2,解得a=-1.
答案: -1例2.若直线l的倾斜角为45°,且在y轴上的截距为1,则直线l的斜截式方程为____________.?
【解析】因为k=tan 45°=1,直线l在y轴上截距为1,故直线l的方程为y=x+1.
答案:y=x+1【解析】因为直线的方程为y=- x+1,所以k=- ,倾斜角为120°,
由题知所求直线的倾斜角为30°,即斜率为 .
因为所求直线在y轴上的截距为-5,
所以由斜截式知所求直线方程为y= x-5.变式训练2.求倾斜角是直线y=- x+1的倾斜角的 ,且满足在y轴上的截距是-5的直线方程.
课后练习1.方程y=ax- 表示的直线可能是 ( )【解析】选C.由方程y=ax- 表示的直线,当a>0时,斜率k=a>0,在y轴上的截距为- <0,都不符合此条件.
当a<0时,斜率k=a<0,在y轴上的截距为- >0,只有C符合此条件.2.已知直线l的斜率为 ,且和两坐标轴围成的三角
形的面积为3,求直线l的方程.【解析】设l的方程为y= x+b,分别令x=0,y=0得y=b,x=-6b,
依题意有 ×|b|×|-6b|=3,所以b2=1,
解得b=±1,
所以l的方程为y= x+1或y= x-1.(三)两条直线的平行与垂直的应用
例1.已知直线l1:y=-x+2a与直线l2:y=(a2-2)x+2.
(1)当a为何值时,l1∥l2?(2)当a为何值时,l1⊥l2?【解析】设直线l1,l2斜率分别为k1,k2,
则k1=-1,k2=a2-2.
(1)当l1∥l2时,有 解得a=-1.
(2)当l1⊥l2时,k1k2=-1,即a2-2=1,
所以a2=3,所以a=
变式训练1.已知直线l1:x-my-6=0,l2:(m-2)x-3y-2m=0.若l1⊥l2,则m的值为__________.若l1∥l2,则m的值为__________.?【解析】由两直线垂直可得:1·(m-2)+m·3=0,解得m= ,
故当l1⊥l2时,m= ;由平行的条件可得:
由 解得m=-1或m=3;
而当m=3时,l1与l2重合,不满足题意,舍去,
故m=-1.
答案: ,-1例2.已知直线l1的方程为y=-2x+3.
(1)若直线l2与l1平行,且过点(-1,3),求直线l2的方程.
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.【解析】(1)由直线l2与l1平行,可设l2的方程为y=-2x+b,将x=-1,y=3代入,得3=(-2)×(-1)+b,即得b=1,
所以直线l2的方程为y=-2x+1.(2)由直线l2与l1垂直,可设l2的方程为y= x+m,
令y=0,得x=-2m,令x=0,得y=m,
故三角形面积S= |-2m|·|m|=4,
所以m2=4,解得m=±2,所以直线l2的方程是y= x+2或y= x-2.课后练习 1.当a为何值时,
(1)两直线y=(a+1)x-2与y=(a-1)x+1互相垂直?
(2)两直线y=-x+4a与y=(a2-2)x+4互相平行?【解析】(1)因为两直线y=(a+1)x-2与y=(a-1)x+1互相垂直,
所以(a+1)(a-1)=-1,即a=0.
(2)因为两直线y=-x+4a与y=(a2-2)x+4互相平行.
所以 即a=-1.(四)直线方程的两点式
观察如图所示的直线l,思考下列问题:
1.直线l经过点P1(x1,y1),P2(x2,y2)(其中x1≠x2)两点,那么直线l的点斜式方程是什么? 提示:由x1≠x2,所求直线的斜率为k= ,则直线的点斜式方程为y-y1= (x-x1).2.方程y-y1= (x-x1)(x1≠x2)能否写成
提示:当y1≠y2时,可以写成上式;当y1=y2时,不能
写成该形式.结论:两点式方程的形式_________ (x1≠x2,y1≠y2),当x1=x2时,方程
为_ ___,当y1=y2时,方程为__ __.x=x1y=y1例1.经过两点(x1,y1),(x2,y2)的直线方程都可以表示为( ) C.(y-y1)(x2-x1)=(x-x1)(y2-y1)
D.y-y1= 【解析】选C.当x1≠x2,y1≠y2时,由两点式可得直线方程为:
化为:(y-y1)(x2-x1)=(x-x1)(y2-y1),对于x1=x2或y1=y2时上述方程也成立,
因此直线方程为:(y-y1)(x2-x1)=(x-x1)(y2-y1).
变式训练1:过点A(2,3)和点B(4,7)的直线方程是( )
A.y=-2x+7 B.y=2x+1 C.y=2x-1 D.y=2
【解析】选C.直线的两点式方程为 即y=2x-1变式训练1.在△ABC中,已知点A(5,-2),B(7,3)且边AC的中点M在y轴上,边BC的中点N在x轴上.(1)求点C的坐标.(2)求直线MN的方程.【解析】(1)设C(x,y)得
因为M在y轴上,N在x轴上,所以 ,解得x=-5,y=-3.
所以C点坐标为(-5,-3).(2)由(1)知M ,N(1,0),
所以直线MN的方程为 例2.已知在平面直角坐标系中,△ABC三个顶点坐标分别为A(1,3),B(5,1),C(-1,-1).
(1)求BC边的中线AD所在的直线方程.(2)求AC边的高BH所在的直线方程.【解析】(1)BC中点D的坐标为(2,0),所以直线AD方程为: 化简得y=-3x+6.
(2)因为kAC= =2,BH⊥AC,所以kBH=- ,
所以直线BH方程为:y-1=- (x-5),即y=- x+ .变式训练2.△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0).
(1)求边AC和AB所在直线的方程.
(2)求边AC上的中线BD所在的直线的方程.【解析】(1)因为A(0,4),C(-8,0),所以直线AC的截距式方程为
化简得y= x+4,
因为B(-2,6),A(0,4),
所以由直线的两点式方程,得AB方程为
即y=-x+4.综上所述,边AC所在直线的方程为y= x+4,边AB所在直线的方程为y=-x+4.(2)设点D(x,y),由线段的中点坐标公式,可得
所以AC中点D的坐标为(-4,2),再由直线的两点式方程,得BD所在直线的方程为 化简得y=2x+10,即为所求边AC上的中线BD所在的直线的方程.(五)直线的截距式方程
1.若直线l经过点A(a,0)与点B(0,b),则直线l的两点式方程是什么?
提示:当a≠0且b≠0时,直线l的两点式方程为 2.问题1中的方程有何特点?
提示:直线l与x轴交点的横坐标a叫做直线在x轴上的截距,因此问题1中的方程是由直线在两个坐标轴上的截距确定的.结论:截距式方程的形式:______________________ .例1.若直线l的方程为 =1,则直线l在x轴与y轴
上的截距分别是 ( )
【解析】选B.直线的截距式方程中x的分母为直线在x轴上的截距,y的分母为直线在y轴上的截距.变式训练1:直线 (ab≠0)在y轴上的截距是 ( )
A.a B.b C.-a D.-b【解析】选D.直线 (ab≠0)中,
令x=0,解得y=-b,所以直线 在y轴上的截距为-b.变式训练2.直线l过点(-3,3),且在两坐标轴上的截距之和为12,求直线l的方程.【解析】由题意设直线l的方程为 则a+b=12, ①
又直线l过点(-3,3),所以 ②
联立①②解得
故所求的直线方程为 例2.在x轴、y轴上的截距分别是2,-3的直线方程为( )【解析】选B.在x轴,y轴上的截距分别是2,-3的直线的方程是 变式训练2:过定点(2,3)且在两坐标轴上截距的绝对值相等的直线有n条,则n的值为 ( )
A.1 B.2 C.3 D.以上答案都不对【解析】选C.①若此直线经过原点,则斜率k= ,所以要求的直线方程为3x-2y=0;②当直线不经过原点时,由题意是直线的方程为x±y=a,把(2,3)代入上述直线的方程得2±3=a,解得a=5或-1.所以直线的方程为x+y-5=0,x-y+1=0.
课后练习 1.过点P(-2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形面积为8,这样的直线l一共有 ( )
A.3条 B.2条 C.1条 D.0条【解析】选C.假设存在过点P(-2,2)的直线l,使它与两坐标轴围成的三角形的面积为8,设直线l的方程为: (a<0,b>0),则 即2a-2b=ab.
直线l与两坐标轴在第二象限内围成的三角形面积S=- ab=8,
即ab=-16,联立 解得:a=-4,b=4.
所以直线l的方程为: 即y=x+4,
即这样的直线有且只有一条.
(六)直线方程的一般式
1.平面直角坐标系中的每一条直线l都可以用一个关于x,y的二元一次方程表示吗?提示:可以,当直线l斜率k存在时,在直线l上任取一点P0(x0,y0),其方程为y-y0=k(x-x0),这是关于x,y的二元一次方程,当直线l斜率不存在,即直线l的倾斜角α=90°时,直线的方程为x-x0=0,这也是关于x,y的二元一次方程.2.每一个关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示一条直线
吗?提示:都表示.当B≠0时,方程可变形为y=
它表示过点 (0,- ),斜率为- 的直线,当B=0时,则x=- ,它表示过
(- ,0),垂直于x轴的一条直线,故每一个关于x,y的二元一次方程都表
示一条直线.结论:直线方程的一般式
我们把关于x,y的二元一次方程______________________________ 叫做直线的一般式方程,简称一般式.Ax+By+C=0(其中A,B不同时为0)例1.直线l的方程为Ax+By+C=0,若直线l过原点和第二、四象限,则( )
A.C=0,A>0 B.C=0,A>0,B>0 C.AB<0,C=0 D.AB>0,C=0【解析】 选D.因为直线l过原点,所以C=0.又因为l过第二、四象限,故- <0,所以AB>0.变式训练1:方程2x-3y-1=0在x轴上的截距为____________;在y轴上的截距为____________.?【解析】令x=0,得y=- ,令y=0,得x= ,所以直线在x轴、y轴上的截距分别为 ,- .
答案: - 例2.把直线l的方程2x-3y-6=0化成截距式,指出直线在x轴、y轴上的截距,并画出图形.
【解析】由2x-3y-6=0,得2x-3y=6,即
该直线在x轴、y轴上的截距分别为3与-2,画出图形如
图所示:
变式训练2:本例条件不变,试将直线l的方程化成斜截式并指出它的斜率与截距.
【解析】由2x-3y-6=0得3y=2x-6,
所以y= x-2,其中斜率为 ,截距为-2.
变式训练3.若把本例中的直线方程“2x-3y-6=0”换为“-4x+7y-28=0”,其结论又如何呢?【解析】由-4x+7y-28=0,得-4x+7y=28,即
其中在x轴,y轴上的截距分别为-7与4.
图形如图所示:例3:直线x-y-1=0的倾斜角与其在y轴上的截距分别是 ( )
A.135°,1 B.45°,-1 C.45°,1 D.135°,-1【解析】选B.根据题意,直线的方程为x-y-1=0,变形可得y=x-1,
则其斜率k=1,倾斜角为45°,在y轴上的截距为-1.变式训练4.直线2x-5y-10=0与坐标轴围成三角形的面积为( )
A.5 B.10 C.15 D.20
【解析】选A.直线2x-5y-10=0与坐标轴的交点坐标为(0,-2),(5,0),
所以直线2x-5y-10=0与坐标轴所围成的三角形面积是: ×2×5=5.课后练习 1.数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标是( )A.(-4,0) B.(0,-4) C.(4,0) D.(4,0)或(-4,0)【解析】选A.设C(m,n),由重心坐标公式得,
三角形ABC的重心为
代入欧拉线方程得:
整理得:m-n+4=0 ①AB的中点为(1,2),kAB= AB的中垂线方程为y-2= (x-1),
即x-2y+3=0.
联立 所以△ABC的外心为(-1,1).则(m+1)2+(n-1)2=32+12=10,整理得:m2+n2+2m-2n=8 ②联立①②得:m=-4,n=0或m=0,n=4,m=0,n=4时,B,C重合,舍去.所以顶点C的坐标是(-4,0).2.(1)如果直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0(a∈R)平行,那么a=_____.?
(2)已知直线l1:(k-3)x+(5-k)y+1=0与l2:2(k-3)x-2y+3=0垂直,则k的值是____.?【解析】(1)当a=0时,不符合题意;当a=-1时,不符合题意;
当a≠0且a≠-1时,l1可化为y= l2可化为y=
由题意知 解得a=-2或a=1.答案:-2或1
(2)由l1⊥l2,得2(k-3)2+(5-k)×(-2)=0,即k2-5k+4=0,解得k=1或k=4.
答案:1或4【总结】利用一般式直线方程判断直线位置关系的方法若直线l1:A1x+B1y+C1=0( ≠0),l2:A2x+B2y+C2=0( ≠0),则:
(1)当A1B2-A2B1≠0时,l1与l2相交.(2)当A1B2-A2B1=0且B1C2-B2C1≠0时,l1∥l2.
(3)当A1B2-A2B1=0且B1C2-B2C1=0时,l1与l2重合.
(4)当A1A2+B1B2=0时,l1⊥l2.3.直线mx+(2m-1)y+1=0和直线3x+my+3=0垂直,则实数m的值为_________.?【解析】本题主要考查两直线垂直关系.若两直线垂直,则有3m+(2m-1)m=0,
即m2+m=0,解得m=0或-1.答案:0或-14.已知三条直线l1:2x+my+2=0(m∈R):l2:2x+y+1=0,l3:x+ny+1=0(n∈R),若l1∥l2,l1⊥l3,则m+n的值为__________.?【解析】因为l1∥l2,所以 =-2,解得m=1.因为l1⊥l3,m=n=0不满足题意,舍去,所以 =-1,解得n=-2.
则m+n=-1.
答案:-1(七)直线方程的综合应用
例1.已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限.
(2)为使直线不经过第二象限,求a的取值范围.【解析】(1)将直线l的方程整理为 所以l的斜率为a,且过定点
而点 在第一象限,故l必过第一象限.(2)直线OA的斜率为 因为l不经过第二象限,
所以a≥3,故a的取值范围是[3,+∞).变式训练1.已知直线l1:2x-y+1=0和直线l2:x+y-4=0相交于点A,O是坐标原点,直线l3经过点A且与OA垂直.
(1)求直线l3的方程.
(2)若点B在直线l3上,且|OB|=10,求点B的坐标.【解析】(1) ?A(1,3),所以kOA=3,得直线l3的斜率是 ,
所以直线l3的方程:y-3= (x-1),即x+3y-10=0.(2)设B(10-3m,m),
由|OB|=10,得 得m=6或0,
所以B(10,0)或B(-8,6).例2.一条光线从点A(3,2)发出,经x轴反射,通过点B(-1,6),求入射光线和反射光线所在直线的方程.
【解析】点A关于x轴的对称点为A1(3,-2),点B关于x轴的对称
点为B1(-1,-6).
因为A1在反射光线的延长线上,B1在入射光线的延长线上,由两点式可得直线A1B的方程为 化简得2x+y-4=0;直线AB1的方程为
化简得2x-y-4=0.
所以入射光线所在直线方程为2x-y-4=0,
反射光线所在直线方程为2x+y-4=0.
变式训练2.已知有条光线从点A(-2,1)出发射向x轴点B,经过x轴反射后射向y轴上的C点,再经过y轴反射后到达点D(-2,7).求直线BC的方程.【解析】如图所示,因为A(-2,1),所以A点关于x轴的对称点为A′(-2,-1),因为D(-2,7),所以D点关于y轴的对称点D′(2,7).
由对称性可得,A′、D′所在直线方程即为BC所在
直线方程,所以直线BC的方程为
整理得2x-y+3=0.变式训练3.已知光线通过点A(2,3),经直线x+y+1=0反射,其反射光线通过点B(1,1),求入射光线和反射光线所在直线方程.【解析】求得点A(2,3)关于直线x+y+1=0的对称点A′(-4,-3).
则由两点式求得反射光线所在的直线A′B的方程为
由 求得直线A′B与直线x+y+1=0的交点
由两点式求得入射光线所在的直线AC的方程为
综上,入射光线所在直线方程为
反射光线所在直线方程为
谢谢!
