人教版必修二3.3.3交点坐标及两点间距离课件(25张)
文档属性
| 名称 | 人教版必修二3.3.3交点坐标及两点间距离课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 624.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 10:54:23 | ||
图片预览








文档简介
课件25张PPT。第三章 直线与方程
习题课 交点坐标及两点间距离
学习目标
1.能熟练求出两直线的交点坐标.
2.理解直线过定点的含义.
3.能解决简单的对称问题.
4.体会坐标法的基本思想.
知识梳理知识点一 两直线的交点坐标 已知直线:l1:A1x+B1y+C1=0;l2:A2x+B2y+C2=0,点A(a,b).
(1)若点A在直线l:Ax+By+C=0上,则有: .
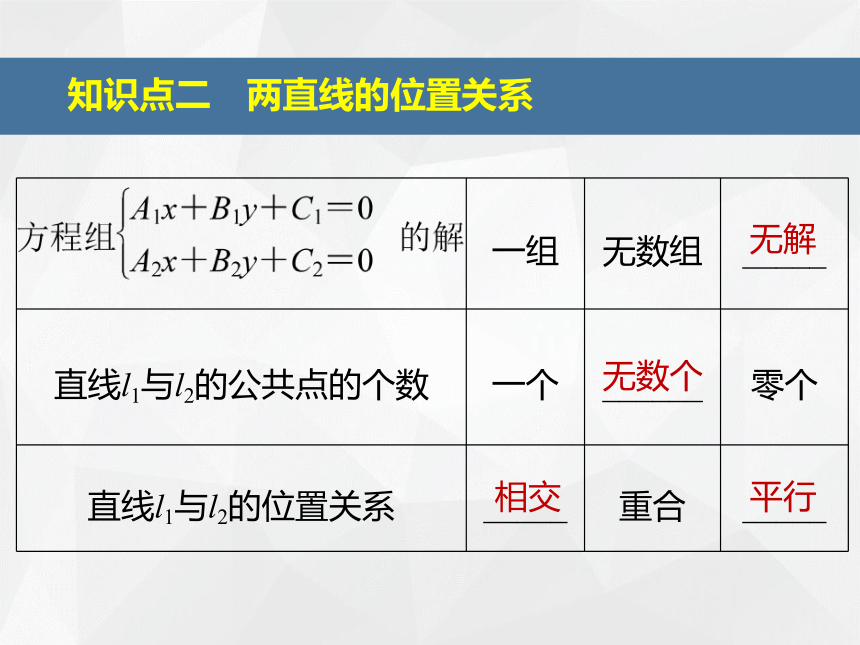
(2)若点A是直线l1与l2的交点,则有:Aa+Bb+C=0知识点二 两直线的位置关系 无解无数个相交平行知识点三 两点间的距离公式 (1)条件:点P1(x1,y1),P2(x2,y2).
(2)结论:__________________________.
(3)特例:点P(x,y)到原点O(0,0)的距离|OP|=
____ __ _.
题型探究 之对称问题命题角度1 关于点对称问题例1 (1)求点P(x0,y0)关于点A(a,b)的对称点P′的坐标;
解 根据题意可知点A(a,b)为PP′的中点,
设P′点的坐标为(x,y), 所以点P′的坐标为(2a-x0,2b-y0).(2)求直线3x-y-4=0关于点(2,-1)的对称直线l的方程.解 方法一 设直线l上任意一点M的坐标为(x,y),
则此点关于点(2,-1)的对称点为M1(4-x,-2-y),
且M1在直线3x-y-4=0上,
所以3(4-x)-(-2-y)-4=0,
即3x-y-10=0.
所以所求直线l的方程为3x-y-10=0.方法二 在直线3x-y-4=0上取两点A(0,-4),
B(1,-1),
则点A(0,-4)关于点(2,-1)的对称点为A1(4,2),
点B(1,-1)关于点(2,-1)的对称点为B1(3,-1).
可得直线A1B1的方程为3x-y-10=0,
即所求直线l的方程为3x-y-10=0. 反思与感悟(1)点关于点的对称问题:若两点A(x1,y1),B(x2,y2)关于点P(x0,y0)对称,则P是线段AB的中点,(2)直线关于点的对称问题:若两条直线l1,l2关于点P对称,则:①l1上任意一点关于点P的对称点必在l2上,反过来,l2上任意一点关于点P的对称点必在l1上;②若l1∥l2,则点P到直线l1,l2的距离相等;③过点P作一直线与l1,l2分别交于A,B两点,则点P是线段AB的中点.跟踪训练1 与直线2x+3y-6=0关于点(1,-1)对称的直线方程是
A.3x-2y+2=0
B.2x+3y+7=0
C.3x-2y-12=0
D.2x+3y+8=0D解析 由平面几何知识易知所求直线与已知直线
2x+3y-6=0平行,
则可设所求直线方程为2x+3y+C=0.
在直线2x+3y-6=0上任取一点(3,0),
关于点(1,-1)的对称点为(-1,-2),
则点(-1,-2)必在所求直线上,
∴2×(-1)+3×(-2)+C=0,C=8.
∴所求直线方程为2x+3y+8=0. 命题角度2 关于轴对称问题 例2(1)点P(-3,4)关于直线x+y-2=0的对称点Q的坐标是
A.(-2, 1) B.(-2, 5)
C.(2,-5) D.(4,-3)
解析 设对称点坐标为(a,b),(2)在平面直角坐标系中,直线y=2x+1关于y=x-2对称的直线l的方程为
A.x-4y-11=0 B.4x-y+11=0
C.x-2y+7=0 D.x-2y-7=0解析 ∵直线y=2x+1关于y=x-2对称的直线是直线l,∴直线l过点(-3,-5).
在直线y=2x+1上取一点A(0,1),
设点A关于y=x-2对称的点为B(a,b),
则点B在直线l上.反思与感悟(1)点关于直线的对称问题
求P(x0,y0)关于Ax+By+C=0的对称点P′(x,y)时,(2)直线关于直线的对称问题:若两条直线l1,l2关于直线l对称,①l1上任意一点关于直线l的对称点必在l2上,反过来,l2上任意一点关于直线l的对称点必在l1上;②过直线l上的一点P且垂直于直线l作一直线与l1,l2分别交于点A,B,则点P是线段AB的中点. 跟踪训练2:试求直线 关于直
线 对称的直线的方程。跟踪训练3 一束光线从原点O(0,0)出发,经过直线l:8x+6y=25反射后通过点P(-4,3),求反射光线的方程.规律与方法 有关对称问题的两种主要类型
(1)中心对称②直线关于点的对称可转化为点关于点的对称问题来解决.
(2)轴对称
①点A(a,b)关于直线Ax+By+C=0(B≠0)的对称点为A′
(m,n),则有②直线关于直线的对称可转化为点关于直线的对称问题来解决. 谢谢聆听!
学习目标
1.能熟练求出两直线的交点坐标.
2.理解直线过定点的含义.
3.能解决简单的对称问题.
4.体会坐标法的基本思想.
知识梳理知识点一 两直线的交点坐标 已知直线:l1:A1x+B1y+C1=0;l2:A2x+B2y+C2=0,点A(a,b).
(1)若点A在直线l:Ax+By+C=0上,则有: .
(2)若点A是直线l1与l2的交点,则有:Aa+Bb+C=0知识点二 两直线的位置关系 无解无数个相交平行知识点三 两点间的距离公式 (1)条件:点P1(x1,y1),P2(x2,y2).
(2)结论:__________________________.
(3)特例:点P(x,y)到原点O(0,0)的距离|OP|=
____ __ _.
题型探究 之对称问题命题角度1 关于点对称问题例1 (1)求点P(x0,y0)关于点A(a,b)的对称点P′的坐标;
解 根据题意可知点A(a,b)为PP′的中点,
设P′点的坐标为(x,y), 所以点P′的坐标为(2a-x0,2b-y0).(2)求直线3x-y-4=0关于点(2,-1)的对称直线l的方程.解 方法一 设直线l上任意一点M的坐标为(x,y),
则此点关于点(2,-1)的对称点为M1(4-x,-2-y),
且M1在直线3x-y-4=0上,
所以3(4-x)-(-2-y)-4=0,
即3x-y-10=0.
所以所求直线l的方程为3x-y-10=0.方法二 在直线3x-y-4=0上取两点A(0,-4),
B(1,-1),
则点A(0,-4)关于点(2,-1)的对称点为A1(4,2),
点B(1,-1)关于点(2,-1)的对称点为B1(3,-1).
可得直线A1B1的方程为3x-y-10=0,
即所求直线l的方程为3x-y-10=0. 反思与感悟(1)点关于点的对称问题:若两点A(x1,y1),B(x2,y2)关于点P(x0,y0)对称,则P是线段AB的中点,(2)直线关于点的对称问题:若两条直线l1,l2关于点P对称,则:①l1上任意一点关于点P的对称点必在l2上,反过来,l2上任意一点关于点P的对称点必在l1上;②若l1∥l2,则点P到直线l1,l2的距离相等;③过点P作一直线与l1,l2分别交于A,B两点,则点P是线段AB的中点.跟踪训练1 与直线2x+3y-6=0关于点(1,-1)对称的直线方程是
A.3x-2y+2=0
B.2x+3y+7=0
C.3x-2y-12=0
D.2x+3y+8=0D解析 由平面几何知识易知所求直线与已知直线
2x+3y-6=0平行,
则可设所求直线方程为2x+3y+C=0.
在直线2x+3y-6=0上任取一点(3,0),
关于点(1,-1)的对称点为(-1,-2),
则点(-1,-2)必在所求直线上,
∴2×(-1)+3×(-2)+C=0,C=8.
∴所求直线方程为2x+3y+8=0. 命题角度2 关于轴对称问题 例2(1)点P(-3,4)关于直线x+y-2=0的对称点Q的坐标是
A.(-2, 1) B.(-2, 5)
C.(2,-5) D.(4,-3)
解析 设对称点坐标为(a,b),(2)在平面直角坐标系中,直线y=2x+1关于y=x-2对称的直线l的方程为
A.x-4y-11=0 B.4x-y+11=0
C.x-2y+7=0 D.x-2y-7=0解析 ∵直线y=2x+1关于y=x-2对称的直线是直线l,∴直线l过点(-3,-5).
在直线y=2x+1上取一点A(0,1),
设点A关于y=x-2对称的点为B(a,b),
则点B在直线l上.反思与感悟(1)点关于直线的对称问题
求P(x0,y0)关于Ax+By+C=0的对称点P′(x,y)时,(2)直线关于直线的对称问题:若两条直线l1,l2关于直线l对称,①l1上任意一点关于直线l的对称点必在l2上,反过来,l2上任意一点关于直线l的对称点必在l1上;②过直线l上的一点P且垂直于直线l作一直线与l1,l2分别交于点A,B,则点P是线段AB的中点. 跟踪训练2:试求直线 关于直
线 对称的直线的方程。跟踪训练3 一束光线从原点O(0,0)出发,经过直线l:8x+6y=25反射后通过点P(-4,3),求反射光线的方程.规律与方法 有关对称问题的两种主要类型
(1)中心对称②直线关于点的对称可转化为点关于点的对称问题来解决.
(2)轴对称
①点A(a,b)关于直线Ax+By+C=0(B≠0)的对称点为A′
(m,n),则有②直线关于直线的对称可转化为点关于直线的对称问题来解决. 谢谢聆听!
