人教版必修二4.2.1直线与圆的位置课件(23张)
文档属性
| 名称 | 人教版必修二4.2.1直线与圆的位置课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 417.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-16 11:15:19 | ||
图片预览





文档简介
课件23张PPT。直线与圆的位置关系本节课学习目标:1、理解并能判断直线和圆的三种位置关系
2、学会在动态的问题中解决最值问题
3、能熟练的求直线的相切线方程和切线长
4、能熟练的解决直线与圆相交的有相关问题复习
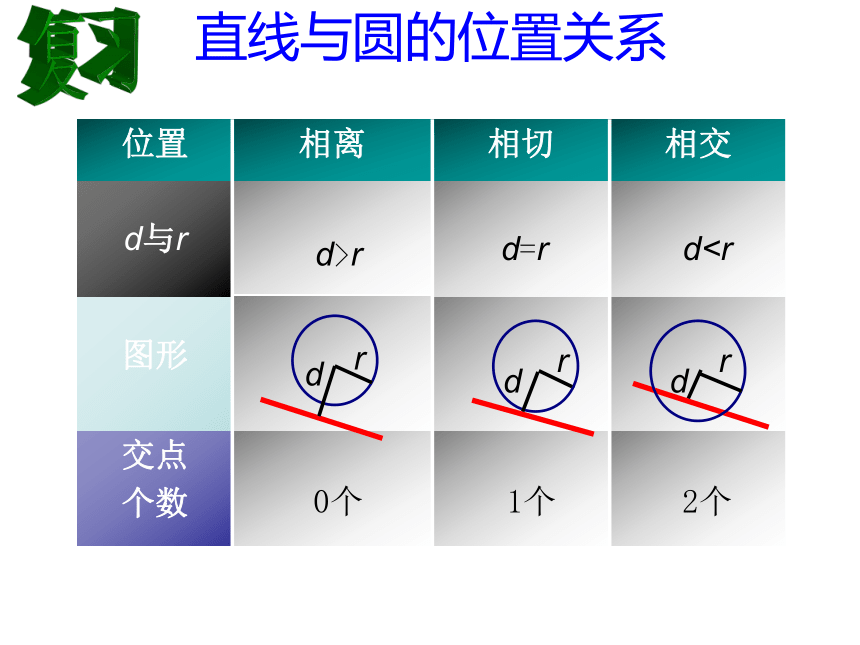
2个
1个
0个
dd=r
d>r
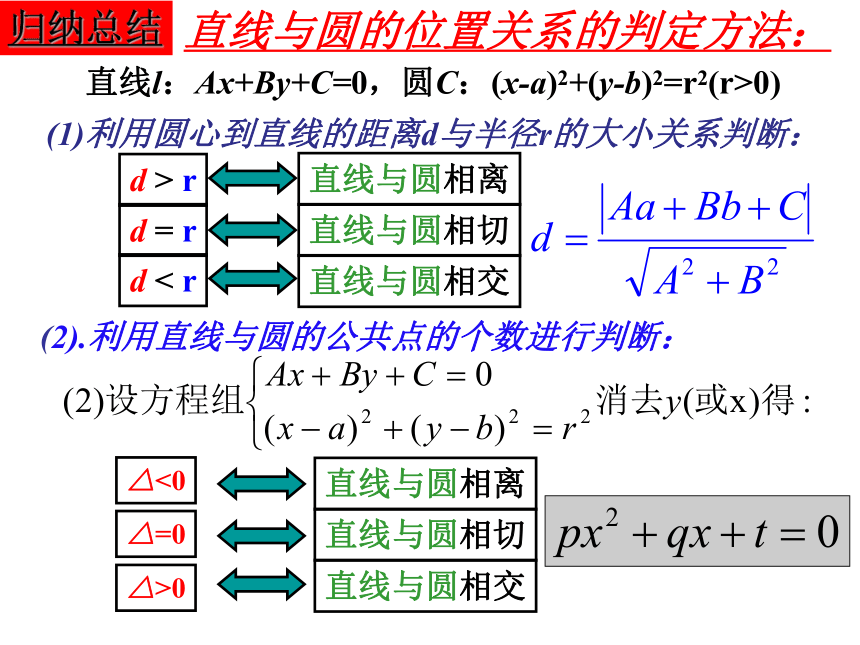
直线与圆的位置关系复习1(1)利用圆心到直线的距离d与半径r的大小关系判断:直线与圆的位置关系的判定方法:归纳总结(2).利用直线与圆的公共点的个数进行判断: 1、直线x+y+2=0与圆x2+(y+1)2=a没有公共点,则a的取值范围是________.
解析:
圆心(0,-1)到直线x+y+2=0的距离为
由题意知 .
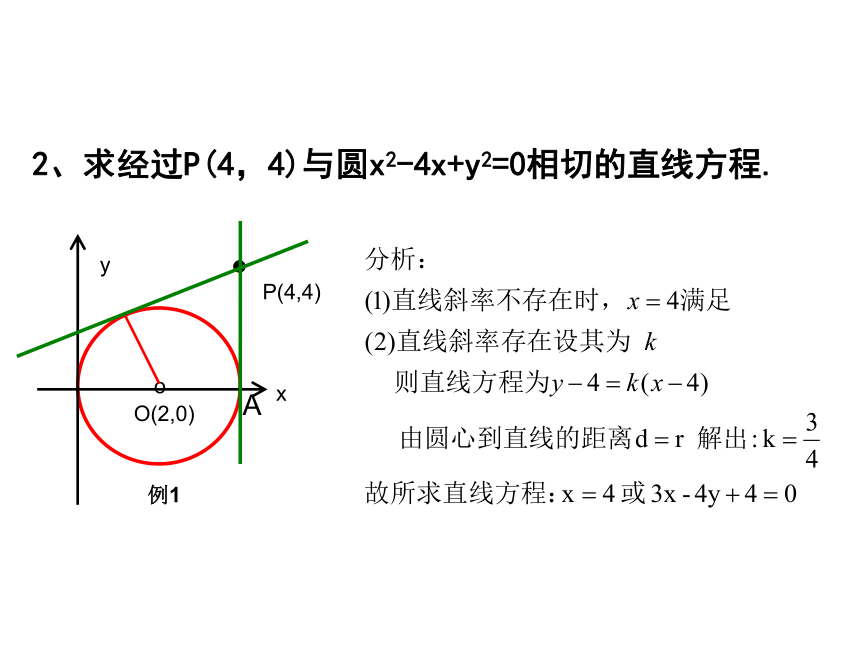
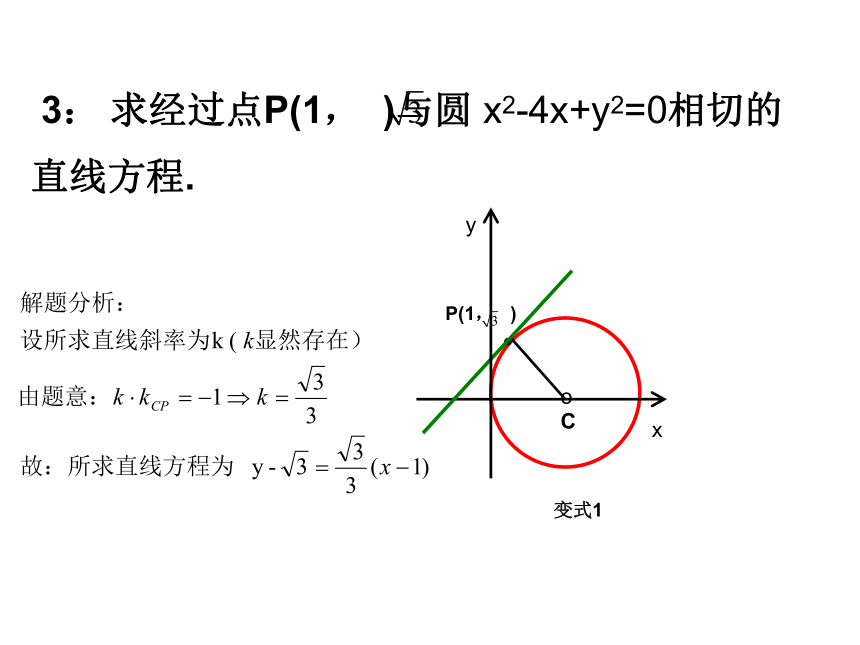
答案 【课前检测】2、求经过P(4,4)与圆x2-4x+y2=0相切的直线方程.P(4,4)oxyO(2,0)例1AxyoP(1, )变式1 3: 求经过点P(1, )与圆 x2-4x+y2=0相切的直线方程.CP(4,4)oxyC(2,0)例1xyoP(1, )变式1点在 圆外,所得切线有两条点在圆上,所得切线有一条点的位置不同归纳解题步骤②设切线方程④化简方程解出k①判断点P在圆上还是圆外③根据圆心到直线距离等于半径列等式:(注意讨论斜率不存在的情况)方法归纳:直线与圆相切问题求直线方程【例题分析】 一、直线与圆相切问题二、直线和圆相交弦长问题1.弦长的求法(1)设弦长为l,弦心距为d,半径为r,
则有 ,
即半弦长,弦心距,半径构成直角三角形,
数形结合,利用勾股定理求解.
二、直线和圆相交弦长问题1.弦长的求法(2)求出交点坐标,利用两点间距离公式,求出弦长;【例题分析】ABxyOM思路分析:1、一直线经过点P(4,5)被圆
截得的弦长为2,求此直线的方程.【当堂检测】2、一只小蚂蚁在圆(x-5)2+(y-3)2=9上环行,它走到哪个位置时与直线l :3x+4y-2=0的距离最短。请你帮小蚂蚁找到这个点并计算这个点到直线l的距离。 p.②设直线方程④化简方程解出k①判断所求直线有多少条③圆心到直线距离,半径,弦长的一半构成直角三角形。根据垂径定理列等式:(注意斜率不存在的情况)方法归纳三、小结1、本节课我们复习了哪些内容?直线与圆位置关系的定义与判定
相离最值问题、相切问题、相交弦问题2、直线与圆相交弦有什么注意事项?几何法与代数法 (体会在圆这儿几何法的简洁)
设直线方程时需要讨论直线斜率是否存在3、本节课用到哪些数学思想?数形结合、分类讨论、化归转化 等
知识像一艘船让它载着我们驶向理想的彼岸...谢谢比较:几何法比代数法运算量少,简便。
2个
1个
0个
d
d>r
直线与圆的位置关系复习1(1)利用圆心到直线的距离d与半径r的大小关系判断:直线与圆的位置关系的判定方法:归纳总结(2).利用直线与圆的公共点的个数进行判断: 1、直线x+y+2=0与圆x2+(y+1)2=a没有公共点,则a的取值范围是________.
解析:
圆心(0,-1)到直线x+y+2=0的距离为
由题意知 .
答案 【课前检测】2、求经过P(4,4)与圆x2-4x+y2=0相切的直线方程.P(4,4)oxyO(2,0)例1AxyoP(1, )变式1 3: 求经过点P(1, )与圆 x2-4x+y2=0相切的直线方程.CP(4,4)oxyC(2,0)例1xyoP(1, )变式1点在 圆外,所得切线有两条点在圆上,所得切线有一条点的位置不同归纳解题步骤②设切线方程④化简方程解出k①判断点P在圆上还是圆外③根据圆心到直线距离等于半径列等式:(注意讨论斜率不存在的情况)方法归纳:直线与圆相切问题求直线方程【例题分析】 一、直线与圆相切问题二、直线和圆相交弦长问题1.弦长的求法(1)设弦长为l,弦心距为d,半径为r,
则有 ,
即半弦长,弦心距,半径构成直角三角形,
数形结合,利用勾股定理求解.
二、直线和圆相交弦长问题1.弦长的求法(2)求出交点坐标,利用两点间距离公式,求出弦长;【例题分析】ABxyOM思路分析:1、一直线经过点P(4,5)被圆
截得的弦长为2,求此直线的方程.【当堂检测】2、一只小蚂蚁在圆(x-5)2+(y-3)2=9上环行,它走到哪个位置时与直线l :3x+4y-2=0的距离最短。请你帮小蚂蚁找到这个点并计算这个点到直线l的距离。 p.②设直线方程④化简方程解出k①判断所求直线有多少条③圆心到直线距离,半径,弦长的一半构成直角三角形。根据垂径定理列等式:(注意斜率不存在的情况)方法归纳三、小结1、本节课我们复习了哪些内容?直线与圆位置关系的定义与判定
相离最值问题、相切问题、相交弦问题2、直线与圆相交弦有什么注意事项?几何法与代数法 (体会在圆这儿几何法的简洁)
设直线方程时需要讨论直线斜率是否存在3、本节课用到哪些数学思想?数形结合、分类讨论、化归转化 等
知识像一艘船让它载着我们驶向理想的彼岸...谢谢比较:几何法比代数法运算量少,简便。
