人教版必修三阅读与思考 相关关系的强与弱课件(16张)
文档属性
| 名称 | 人教版必修三阅读与思考 相关关系的强与弱课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 949.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-17 08:37:34 | ||
图片预览




文档简介
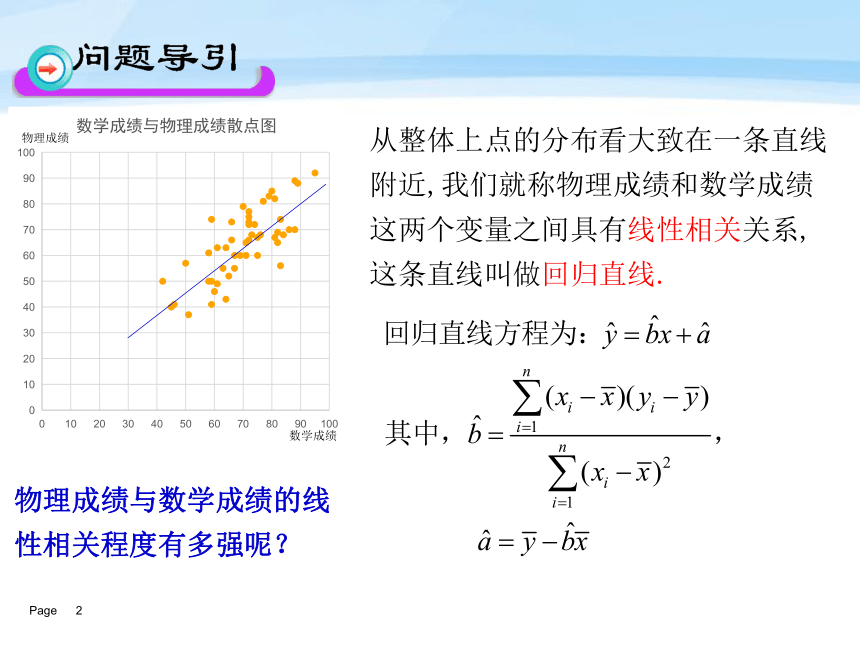
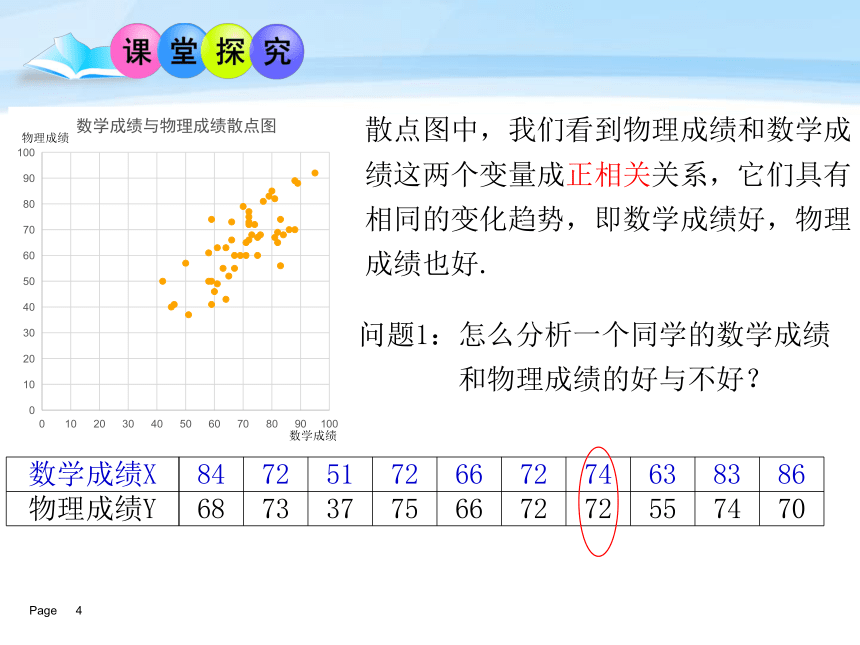
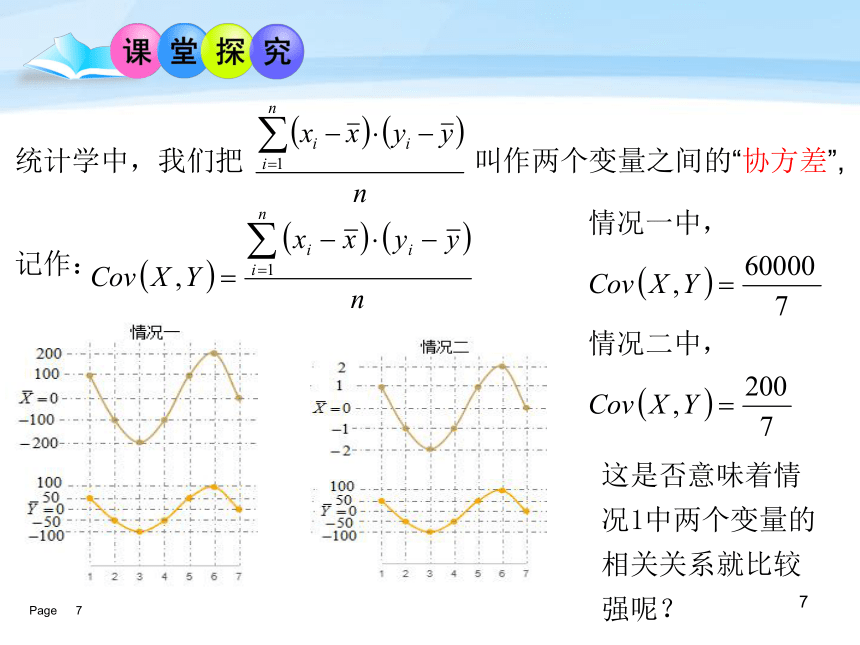
课件16张PPT。有些老师常说:“如果你的数学成绩好,那么你的物理学习就不会有什么大问题.” 按照这种说法,似乎学生的物理成绩与数学成绩之间存在着一种相关关系。为了研究数学成绩和物理成绩这种相关关系,现抽取某次考试中一个班级(共50名学生)的数学成绩与物理成绩.从整体上点的分布看大致在一条直线附近,我们就称物理成绩和数学成绩这两个变量之间具有线性相关关系,这条直线叫做回归直线.数学成绩物理成绩物理成绩与数学成绩的线性相关程度有多强呢?相关关系的强与弱散点图中,我们看到物理成绩和数学成绩这两个变量成正相关关系,它们具有相同的变化趋势,即数学成绩好,物理成绩也好.数学成绩物理成绩问题1:怎么分析一个同学的数学成绩
和物理成绩的好与不好?问题2:
怎么从数据上说明随着数学成绩的增加,物理成绩也增加呢?7统计学中,我们把 叫作两个变量之间的“协方差”,
记作:这是否意味着情况1中两个变量的相关关系就比较强呢?8相关关系的强与弱还与
每个变量整体的偏离水平有关系,即还要考虑它们各自的标准差.除以标准差,
就是把变量变化的幅度对
相关程度的影响剔除掉了.相关系数统计中用相关系数 来衡量两个变量之间线性关系的强弱.
若相应于变量 的取值 ,变量 的观测值为 ,
则两个变量的相关系数的计算公式为:(1)当 时,表明变量 与
当 时,表明变量 与 负相关.正相关.(2)当 越大时,表明变量 与 的相关关系 越强.思考:
相关系数取值
范围是多少?统计学认为,对于两个变量, 说明物理成绩与数学成绩的正相关性很强.图1的r=0.97,这些点有明显的从左下角到右上角沿直线分布趋势,
这时用线性回归模型描述两个变量之间的关系效果很好;图2的r=-0.85,这时用线性回归模型描述两个变量之间的关系效果也较好;图3的r=0.24,图4的r=-0.05,
这些点的分布几乎没有什么规则,这时不能用线性回归模型描述这两个变量之间的关系.例题讲解2.注意:(2)1.统计中用相关系数 来衡量两个变量之间线性关系的强弱.
和物理成绩的好与不好?问题2:
怎么从数据上说明随着数学成绩的增加,物理成绩也增加呢?7统计学中,我们把 叫作两个变量之间的“协方差”,
记作:这是否意味着情况1中两个变量的相关关系就比较强呢?8相关关系的强与弱还与
每个变量整体的偏离水平有关系,即还要考虑它们各自的标准差.除以标准差,
就是把变量变化的幅度对
相关程度的影响剔除掉了.相关系数统计中用相关系数 来衡量两个变量之间线性关系的强弱.
若相应于变量 的取值 ,变量 的观测值为 ,
则两个变量的相关系数的计算公式为:(1)当 时,表明变量 与
当 时,表明变量 与 负相关.正相关.(2)当 越大时,表明变量 与 的相关关系 越强.思考:
相关系数取值
范围是多少?统计学认为,对于两个变量, 说明物理成绩与数学成绩的正相关性很强.图1的r=0.97,这些点有明显的从左下角到右上角沿直线分布趋势,
这时用线性回归模型描述两个变量之间的关系效果很好;图2的r=-0.85,这时用线性回归模型描述两个变量之间的关系效果也较好;图3的r=0.24,图4的r=-0.05,
这些点的分布几乎没有什么规则,这时不能用线性回归模型描述这两个变量之间的关系.例题讲解2.注意:(2)1.统计中用相关系数 来衡量两个变量之间线性关系的强弱.
