人教版选修三2.3.1变量间的相关关系课件(22张)
文档属性
| 名称 | 人教版选修三2.3.1变量间的相关关系课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 397.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-17 08:38:08 | ||
图片预览







文档简介
课件22张PPT。变量间的相关关系一、变量之间的相关关系思考: 我们经常听到有这样的说法“如果你的数学成绩好,那么你的物理学习就不会有什么大问题。”
按照这种说法,似乎学生的物理成绩与数学成绩之间存在着一种相关关系(相互关系)。这种说法有没有根据呢?分析:
物理成绩和数学成绩是两个变量,从经验看,由于物理课程涉及比较多的数学知识。数学成绩的高低对物理成绩的高低是有一定影响的。但决非唯一因素,还有其它因素,如是否喜欢物理,用在物理学习上的时间等等。
总结:
不能通过一个人的数学成绩是多少就准确地断定他的物理成绩能达到多少。这种关系不像销售额与销售量的关系(销售额=销售量×价格)是确定型的,这两个变量之间存在一定的相互关系,它们之间是一种不确定型的关系。
要找到他们的关系,就需要收集大量的数据,对数据进行统计分析,分析其中的规律,才能对他们之间的关系作出判断.变量间的相关关系在我们的生活中广泛存在:
如: (1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系
(3)人体内脂肪含量与年龄之间的关系2、两个变量之间产生相关关系的原因是受许多不确定的随机因素的影响.1. 变量之间除了函数关系外,还有相关关系.(一)相关关系的概念:
两个变量之间的关系可能是确定的关系(如:函数关系),或非确定性关系。
当自变量取值一定时,因变量也确定,则为确定关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系。
相关关系是一种非确定性关系。
如何研究这种变量间的相关关系呢?
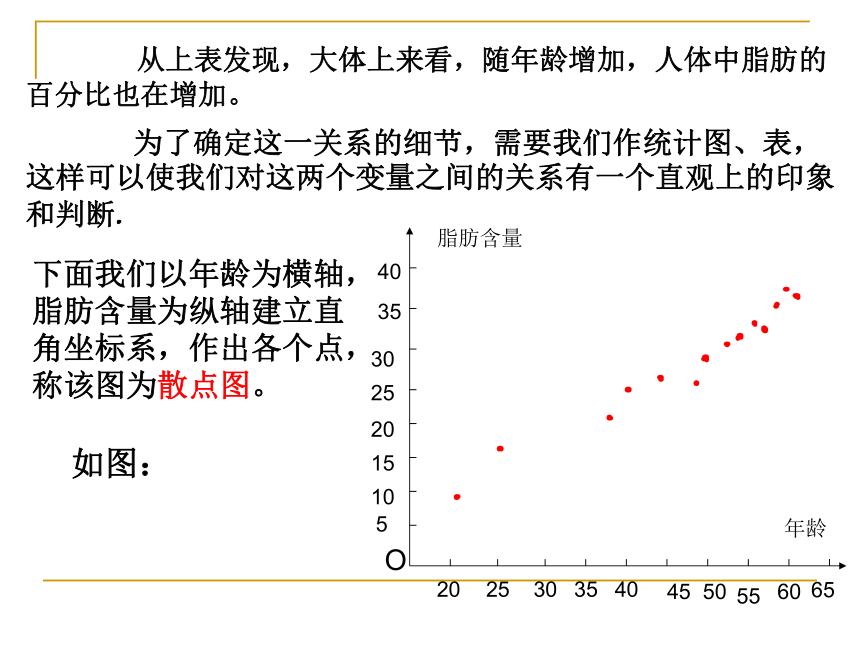
通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断.探究一 根据上述数据,人体的脂肪含量和年龄之间有怎样的关系?二、两个变量的线性相关 从上表发现,大体上来看,随年龄增加,人体中脂肪的百分比也在增加。 下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
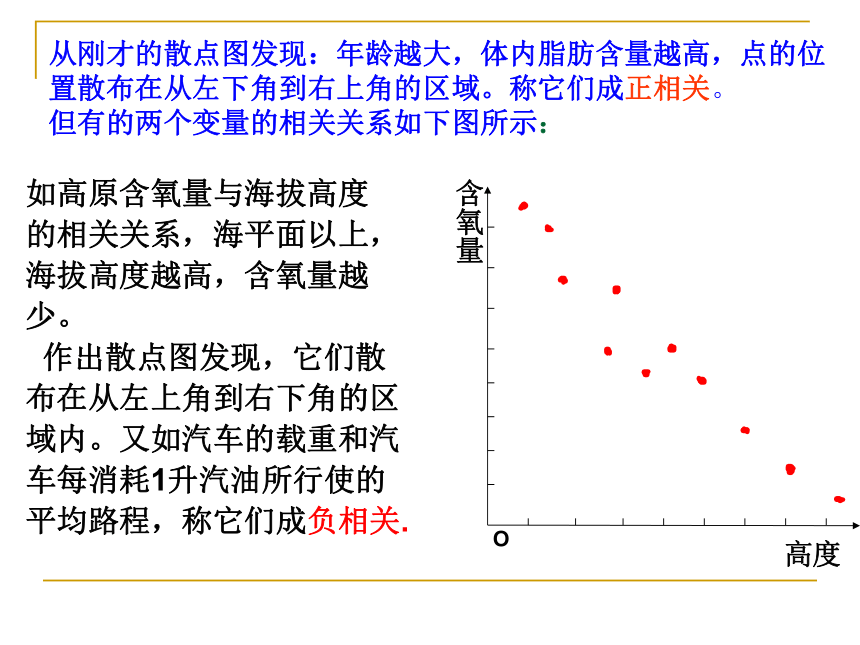
称该图为散点图。如图: 为了确定这一关系的细节,需要我们作统计图、表,这样可以使我们对这两个变量之间的关系有一个直观上的印象和判断. 从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。 但有的两个变量的相关关系如下图所示:如高原含氧量与海拔高度
的相关关系,海平面以上,
海拔高度越高,含氧量越
少。
作出散点图发现,它们散
布在从左上角到右下角的区
域内。又如汽车的载重和汽
车每消耗1升汽油所行使的
平均路程,称它们成负相关.散点图有了,又该如何寻找这个相关关系呢?
当人的年龄增加时,体内脂肪含量到底是以什么方式增加呢我们再观察它的图像发现这些点大致分布在一条直线附近, 那么,我们该怎样来求出这个回归方程?
20253035404550556065年龄脂肪含量0510152025303540像这样,如果散点图中点的分布从整体上看大致在一条直线
附近,我们就称这两个变量之间具有线性相关关系,这条直线
叫做回归直线,该直线方程简称回归方程。(二)回归直线如何求回归直线的方程探究 实际上,求回归直线的关键是如何用数学的方法来刻画”从整体上看,各点到此直线的距离最小”. 实际上,求回归直线的关键是
如何用数学的方法来刻画“从整体
上看,各点到此直线的距离最小”.为了计算方便,通常用:问题归结为:a,b取什么值时Q最小,即总体偏差最小.下面是计算回归方程的斜率和截距的一般公式.这种通过求总体偏差的最小值而得到回归直线的方法就是最小二乘法.注意:回归方程不是变量x,y之间的真实关系例1:观察两相关变量得如下表:求两变量间的回归直线方程解:例2:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:摄氏温度 -5 0 4 7 12 15 19 23 27 31 36热饮杯数 156 150 132 128 130 116 104 89 93 76 54 (1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律;
(3)求回归方程;
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。解: (1)散点图(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。(3)从散点图可以看出,这些点大致分布在一条直线附近。求样本数据的线性回归方程,可按下列步骤进行:解:(1)散点图如图:由散点图可知,年收入越高,年饮食支出越高,图中点的趋势表明两个变量间也确实存在着线性相关关系.
按照这种说法,似乎学生的物理成绩与数学成绩之间存在着一种相关关系(相互关系)。这种说法有没有根据呢?分析:
物理成绩和数学成绩是两个变量,从经验看,由于物理课程涉及比较多的数学知识。数学成绩的高低对物理成绩的高低是有一定影响的。但决非唯一因素,还有其它因素,如是否喜欢物理,用在物理学习上的时间等等。
总结:
不能通过一个人的数学成绩是多少就准确地断定他的物理成绩能达到多少。这种关系不像销售额与销售量的关系(销售额=销售量×价格)是确定型的,这两个变量之间存在一定的相互关系,它们之间是一种不确定型的关系。
要找到他们的关系,就需要收集大量的数据,对数据进行统计分析,分析其中的规律,才能对他们之间的关系作出判断.变量间的相关关系在我们的生活中广泛存在:
如: (1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系
(3)人体内脂肪含量与年龄之间的关系2、两个变量之间产生相关关系的原因是受许多不确定的随机因素的影响.1. 变量之间除了函数关系外,还有相关关系.(一)相关关系的概念:
两个变量之间的关系可能是确定的关系(如:函数关系),或非确定性关系。
当自变量取值一定时,因变量也确定,则为确定关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系。
相关关系是一种非确定性关系。
如何研究这种变量间的相关关系呢?
通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断.探究一 根据上述数据,人体的脂肪含量和年龄之间有怎样的关系?二、两个变量的线性相关 从上表发现,大体上来看,随年龄增加,人体中脂肪的百分比也在增加。 下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。如图: 为了确定这一关系的细节,需要我们作统计图、表,这样可以使我们对这两个变量之间的关系有一个直观上的印象和判断. 从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。 但有的两个变量的相关关系如下图所示:如高原含氧量与海拔高度
的相关关系,海平面以上,
海拔高度越高,含氧量越
少。
作出散点图发现,它们散
布在从左上角到右下角的区
域内。又如汽车的载重和汽
车每消耗1升汽油所行使的
平均路程,称它们成负相关.散点图有了,又该如何寻找这个相关关系呢?
当人的年龄增加时,体内脂肪含量到底是以什么方式增加呢我们再观察它的图像发现这些点大致分布在一条直线附近, 那么,我们该怎样来求出这个回归方程?
20253035404550556065年龄脂肪含量0510152025303540像这样,如果散点图中点的分布从整体上看大致在一条直线
附近,我们就称这两个变量之间具有线性相关关系,这条直线
叫做回归直线,该直线方程简称回归方程。(二)回归直线如何求回归直线的方程探究 实际上,求回归直线的关键是如何用数学的方法来刻画”从整体上看,各点到此直线的距离最小”. 实际上,求回归直线的关键是
如何用数学的方法来刻画“从整体
上看,各点到此直线的距离最小”.为了计算方便,通常用:问题归结为:a,b取什么值时Q最小,即总体偏差最小.下面是计算回归方程的斜率和截距的一般公式.这种通过求总体偏差的最小值而得到回归直线的方法就是最小二乘法.注意:回归方程不是变量x,y之间的真实关系例1:观察两相关变量得如下表:求两变量间的回归直线方程解:例2:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:摄氏温度 -5 0 4 7 12 15 19 23 27 31 36热饮杯数 156 150 132 128 130 116 104 89 93 76 54 (1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律;
(3)求回归方程;
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。解: (1)散点图(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。(3)从散点图可以看出,这些点大致分布在一条直线附近。求样本数据的线性回归方程,可按下列步骤进行:解:(1)散点图如图:由散点图可知,年收入越高,年饮食支出越高,图中点的趋势表明两个变量间也确实存在着线性相关关系.
