人教版必修三2.2.2用样本的数字特征估计总体的数字特征课件(35张)
文档属性
| 名称 | 人教版必修三2.2.2用样本的数字特征估计总体的数字特征课件(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-17 00:00:00 | ||
图片预览










文档简介
课件35张PPT。 第二章 统计
2.2.2 用样本的数字特征估计
总体的数字特征1、众数 在一组数据中,出现次数最多的数据叫做这一组数据的众数。2、中位数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。?思考1:在初中我们学过众数、中位数和平均数的概念,这些数据都是反映样本信息的数字特征,对一组样本数据如何求众数、中位数和平均数? (一):众数、中位数和平均数 (一):众数、中位数和平均数 例:某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图,分别求甲乙两人的中球众数,中位数和平均数? 甲 乙
8 0 9
3 2 1 1 3 4 8 9
7 6 5 4 2 0 2 0 1 1 3
7 3甲 无众数,中位数=平均数乙的 无众数是21,中位数=(一):众数、中位数和平均数与频率分布直方图的关系 思考2:在城市居民月均用水量样本数据的频率分布直方图中,你认为众数应在哪个小矩形内?由此估计总体的众数是什么? 思考4:在城市居民月均用水量样本数据的频率分布直
方图中,有50%的个体小于中位数,也有50%的个体大于
中位数。从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.由此
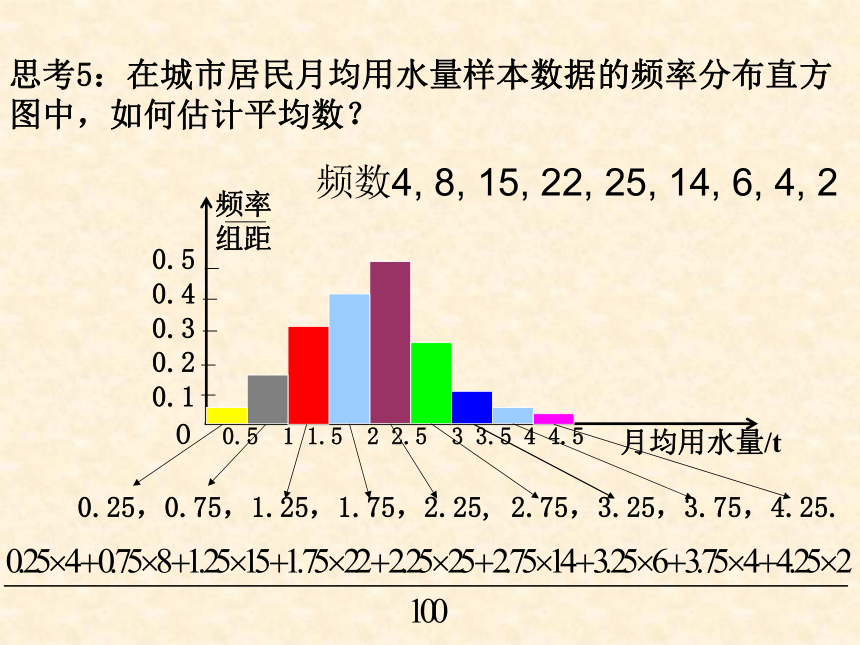
估计总体的中位数是什么? 中位数是2+0.02=2.02. 思考3:如何从频率分布直方图中估计中位数呢?中位数:表示样本数据所占频率的等分线。思考5:在城市居民月均用水量样本数据的频率分布直方图中,如何估计平均数?0.25,0.75,1.25,1.75,2.25, 2.75,3.25,3.75,4.25. 频数4, 8, 15, 22, 25, 14, 6, 4, 2=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+
4.25×0.02
=2.02(t).
平均数是2.02. 频率分布直方图中,平均数的估计值是每个小矩形的面积与小矩形底边中点的横坐标之积相加。思考6:从居民月均用水量样本数据可知,该样本的众数是2.3,中位数是2.0,平均数是1.973,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
众数2.25,中位数2.02,平均数2.02 频率分布直方图损失了一些样本数据,得到的是一个估计值,且所得估值与数据分组有关. 注:在只有样本频率分布直方图的情况下,我们可以按上述方法估计众数、中位数和平均数,并由此估计总体特征. 0 2 3 4 4 5 5 6 6 7 8 8 9
1 0 0 0 0 2 2 2 2 3 3 3 3 4 4 4 5 5 5 5 5 6 6 6 6 6 7 7 7 7 8 8 8 8 8 9 9 9
2 0 0 0 0 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 6 6 6 7 7 8 8 8 9 9
3 1 4 2 3 2 0 7 6 5 8
4 1 3
如:样本数据收集有个别差错不影响中位数;大学
毕业生凭工资中位数找单位可能收入较低.
平均数大于(或小于)中位数,说明样本数据
中存在许多较大(或较小)的极端值.
这句话具有模糊性甚至蒙骗性,其中收入水平
是员工工资的某个中心点,它可以是众数、中位数
或平均数.思考:样本中位数不受少数几个极端值的影响,这在某些情况下是一个优点,但它对极端值的不敏感有时也会成为缺点,你能举例说明吗?
探究:样本数据的平均数大于(或小于)中位数说明什么问题?你怎样理解“我们单位的收入水平比别的单位高”这句话的含义? 例. 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?分析:众数为200,中位数为220,平均数为300。
(2)因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。课堂小结
1.一组数据中的众数可能不止一个也可能没有,平均数和中位数是惟一的,求中位数时必须排序。
2.利用频率分布直方图求数字特征:
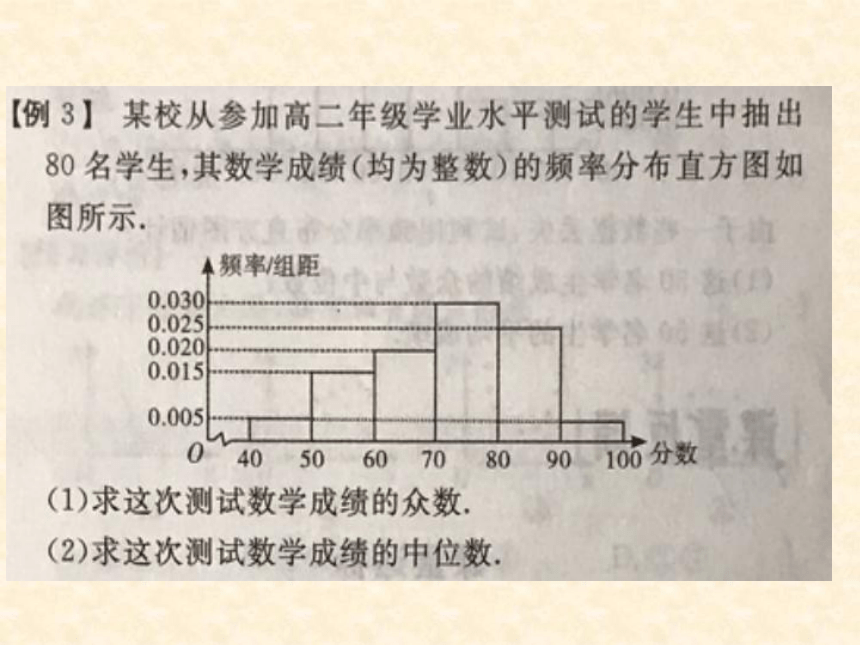
(1)众数是最高的矩形的底边中点。
(2)中位数左右两边的直方图面积之和相等都是0.5.
(3)平均数等于每个小矩形面积乘以对应小矩形底边中点的横坐标之和。
作业:创新设计P34-36(二):标准差 样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息. 平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.当样本数据质量比较差时,使用众数、中位数或平均数描述数据的中心位置,可能与实际情况产生较大的误差,难以反映样本数据的实际状况,因此,我们需要一个统计数字刻画样本数据的离散程度. 思考1:在一次射击选拔赛中,甲、乙两名运动员各射击10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
甲、乙两人本次射击的平均成绩分别为多少环?思考2:甲、乙两人射击的平均成绩相等,观察两人成绩的频率分布条形图,你能说明其水平差异在那里吗?环数甲的成绩比较分散,极差较大,乙的成绩相对集中,比较稳定.环数思考3:对于样本数据x1,x2,…,xn,设想通过各数据到其平均数的平均距离来反映样本数据的分散程度,那么这个平均距离如何计算? 思考4:反映样本数据的分散程度的大小,最常用的统计量是标准差,一般用s表示.假设样本数据x1,x2,…,xn的平均数为 ,则标准差的计算公式是: 那么标准差的取值范围是什么?标准差为0的样本数据有何特点? s≥0,标准差为0的样本数据都相等. 标准差越大离散程度越大,数据较分散;标准差越小离散程度越小,数据较集中在平均数周围. 知识补充1.标准差的平方 称为方差,有时用方差代替标准差测量样本数据的离散度.方差与标准差的测量效果是一致的,在实际应用中一般多采用标准差.2.现实中的总体所包含的个体数往往很多,总体的平均数与标准差是未知的,我们通常用样本的平均数和标准差去估计总体的平均数与标准差,但要求样本有较好的代表性.例1 画出下列四组样本数据的条形图,
说明他们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;样本数字特征例题分析(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
例2 甲、乙两人同时生产内径为25.40mm的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各随机抽取20件,量得其内径尺寸如下(单位:mm):甲 :
25.46 25.32 25.45 25.39 25.36 25.34 25.42 25.45 25.38 25.42 25.39 25.43 25.39 25.40 25.44 25.40 25.42 25.35 25.41 25.39乙:
25.40 25.43 25.44 25.48 25.48 25.47 25.49 25.49 26.36 25.34 25.33 25.43 25.43 25.32 25.47 25.31 25.32 25.32 25.32 25.48 从生产零件内径的尺寸看,谁生产的零件质量较高? 甲生产的零件内径更接近内径标准,且稳定程度较高,故甲生产的零件质量较高. 说明:1.生产质量可以从总体的平均数与标准差两个角度来衡量,但甲、乙两个总体的平均数与标准差都是不知道的,我们就用样本的平均数与标准差估计总体的平均数与标准差.
2.问题中25.40mm是内径的标准值,而不是总体的平均数.例3 以往招生统计显示,某所大学录取的新生高考总分的中位数基本稳定在550分,若某同学今年高考得了520分,他想报考这所大学还需收集哪些信息?要点:(1)查往年录取的新生的平均分数.若平均数小于中位数很多,说明最低录取线较低,可以报考;
(2)查往年录取的新生高考总分的标准差.若标准差较大,说明新生的录取分数较分散,最低录取线可能较低,可以考虑报考.例4 在去年的足球甲A联赛中,甲队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;乙队每场比赛平均失球数是2.1,全年比赛失球个数的标准差为0.4.你认为下列说法是否正确,为什么?
(1)平均来说甲队比乙队防守技术好;(2)乙队比甲队技术水平更稳定;(3)甲队有时表现很差,有时表现又非常好;(4)乙队很少不失球.小结作业1.对同一个总体,可以抽取不同的样本,相应的平均数与标准差都会发生改变.如果样本的代表性差,则对总体所作的估计就会产生偏差;如果样本没有代表性,则对总体作出错误估计的可能性就非常大,由此可见抽样方法的重要性.2.在抽样过程中,抽取的样本是具有随机性的,如从一个包含6个个体的总体中抽取一个容量为3的样本就有20中可能抽样,因此样本的数字特征也有随机性.
用样本的数字特征估计总体的数字特征,是一种统计思想,没有惟一答案.
2.2.2 用样本的数字特征估计
总体的数字特征1、众数 在一组数据中,出现次数最多的数据叫做这一组数据的众数。2、中位数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。?思考1:在初中我们学过众数、中位数和平均数的概念,这些数据都是反映样本信息的数字特征,对一组样本数据如何求众数、中位数和平均数? (一):众数、中位数和平均数 (一):众数、中位数和平均数 例:某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图,分别求甲乙两人的中球众数,中位数和平均数? 甲 乙
8 0 9
3 2 1 1 3 4 8 9
7 6 5 4 2 0 2 0 1 1 3
7 3甲 无众数,中位数=平均数乙的 无众数是21,中位数=(一):众数、中位数和平均数与频率分布直方图的关系 思考2:在城市居民月均用水量样本数据的频率分布直方图中,你认为众数应在哪个小矩形内?由此估计总体的众数是什么? 思考4:在城市居民月均用水量样本数据的频率分布直
方图中,有50%的个体小于中位数,也有50%的个体大于
中位数。从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.由此
估计总体的中位数是什么? 中位数是2+0.02=2.02. 思考3:如何从频率分布直方图中估计中位数呢?中位数:表示样本数据所占频率的等分线。思考5:在城市居民月均用水量样本数据的频率分布直方图中,如何估计平均数?0.25,0.75,1.25,1.75,2.25, 2.75,3.25,3.75,4.25. 频数4, 8, 15, 22, 25, 14, 6, 4, 2=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+
4.25×0.02
=2.02(t).
平均数是2.02. 频率分布直方图中,平均数的估计值是每个小矩形的面积与小矩形底边中点的横坐标之积相加。思考6:从居民月均用水量样本数据可知,该样本的众数是2.3,中位数是2.0,平均数是1.973,这与我们从样本频率分布直方图得出的结论有偏差,你能解释一下原因吗?
众数2.25,中位数2.02,平均数2.02 频率分布直方图损失了一些样本数据,得到的是一个估计值,且所得估值与数据分组有关. 注:在只有样本频率分布直方图的情况下,我们可以按上述方法估计众数、中位数和平均数,并由此估计总体特征. 0 2 3 4 4 5 5 6 6 7 8 8 9
1 0 0 0 0 2 2 2 2 3 3 3 3 4 4 4 5 5 5 5 5 6 6 6 6 6 7 7 7 7 8 8 8 8 8 9 9 9
2 0 0 0 0 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 6 6 6 7 7 8 8 8 9 9
3 1 4 2 3 2 0 7 6 5 8
4 1 3
如:样本数据收集有个别差错不影响中位数;大学
毕业生凭工资中位数找单位可能收入较低.
平均数大于(或小于)中位数,说明样本数据
中存在许多较大(或较小)的极端值.
这句话具有模糊性甚至蒙骗性,其中收入水平
是员工工资的某个中心点,它可以是众数、中位数
或平均数.思考:样本中位数不受少数几个极端值的影响,这在某些情况下是一个优点,但它对极端值的不敏感有时也会成为缺点,你能举例说明吗?
探究:样本数据的平均数大于(或小于)中位数说明什么问题?你怎样理解“我们单位的收入水平比别的单位高”这句话的含义? 例. 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?分析:众数为200,中位数为220,平均数为300。
(2)因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。课堂小结
1.一组数据中的众数可能不止一个也可能没有,平均数和中位数是惟一的,求中位数时必须排序。
2.利用频率分布直方图求数字特征:
(1)众数是最高的矩形的底边中点。
(2)中位数左右两边的直方图面积之和相等都是0.5.
(3)平均数等于每个小矩形面积乘以对应小矩形底边中点的横坐标之和。
作业:创新设计P34-36(二):标准差 样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息. 平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.当样本数据质量比较差时,使用众数、中位数或平均数描述数据的中心位置,可能与实际情况产生较大的误差,难以反映样本数据的实际状况,因此,我们需要一个统计数字刻画样本数据的离散程度. 思考1:在一次射击选拔赛中,甲、乙两名运动员各射击10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
甲、乙两人本次射击的平均成绩分别为多少环?思考2:甲、乙两人射击的平均成绩相等,观察两人成绩的频率分布条形图,你能说明其水平差异在那里吗?环数甲的成绩比较分散,极差较大,乙的成绩相对集中,比较稳定.环数思考3:对于样本数据x1,x2,…,xn,设想通过各数据到其平均数的平均距离来反映样本数据的分散程度,那么这个平均距离如何计算? 思考4:反映样本数据的分散程度的大小,最常用的统计量是标准差,一般用s表示.假设样本数据x1,x2,…,xn的平均数为 ,则标准差的计算公式是: 那么标准差的取值范围是什么?标准差为0的样本数据有何特点? s≥0,标准差为0的样本数据都相等. 标准差越大离散程度越大,数据较分散;标准差越小离散程度越小,数据较集中在平均数周围. 知识补充1.标准差的平方 称为方差,有时用方差代替标准差测量样本数据的离散度.方差与标准差的测量效果是一致的,在实际应用中一般多采用标准差.2.现实中的总体所包含的个体数往往很多,总体的平均数与标准差是未知的,我们通常用样本的平均数和标准差去估计总体的平均数与标准差,但要求样本有较好的代表性.例1 画出下列四组样本数据的条形图,
说明他们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;样本数字特征例题分析(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
例2 甲、乙两人同时生产内径为25.40mm的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各随机抽取20件,量得其内径尺寸如下(单位:mm):甲 :
25.46 25.32 25.45 25.39 25.36 25.34 25.42 25.45 25.38 25.42 25.39 25.43 25.39 25.40 25.44 25.40 25.42 25.35 25.41 25.39乙:
25.40 25.43 25.44 25.48 25.48 25.47 25.49 25.49 26.36 25.34 25.33 25.43 25.43 25.32 25.47 25.31 25.32 25.32 25.32 25.48 从生产零件内径的尺寸看,谁生产的零件质量较高? 甲生产的零件内径更接近内径标准,且稳定程度较高,故甲生产的零件质量较高. 说明:1.生产质量可以从总体的平均数与标准差两个角度来衡量,但甲、乙两个总体的平均数与标准差都是不知道的,我们就用样本的平均数与标准差估计总体的平均数与标准差.
2.问题中25.40mm是内径的标准值,而不是总体的平均数.例3 以往招生统计显示,某所大学录取的新生高考总分的中位数基本稳定在550分,若某同学今年高考得了520分,他想报考这所大学还需收集哪些信息?要点:(1)查往年录取的新生的平均分数.若平均数小于中位数很多,说明最低录取线较低,可以报考;
(2)查往年录取的新生高考总分的标准差.若标准差较大,说明新生的录取分数较分散,最低录取线可能较低,可以考虑报考.例4 在去年的足球甲A联赛中,甲队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;乙队每场比赛平均失球数是2.1,全年比赛失球个数的标准差为0.4.你认为下列说法是否正确,为什么?
(1)平均来说甲队比乙队防守技术好;(2)乙队比甲队技术水平更稳定;(3)甲队有时表现很差,有时表现又非常好;(4)乙队很少不失球.小结作业1.对同一个总体,可以抽取不同的样本,相应的平均数与标准差都会发生改变.如果样本的代表性差,则对总体所作的估计就会产生偏差;如果样本没有代表性,则对总体作出错误估计的可能性就非常大,由此可见抽样方法的重要性.2.在抽样过程中,抽取的样本是具有随机性的,如从一个包含6个个体的总体中抽取一个容量为3的样本就有20中可能抽样,因此样本的数字特征也有随机性.
用样本的数字特征估计总体的数字特征,是一种统计思想,没有惟一答案.
