人教版必修三3.2.2 (整数值)随机数的产生课件(26张)
文档属性
| 名称 | 人教版必修三3.2.2 (整数值)随机数的产生课件(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 186.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-17 08:39:42 | ||
图片预览







文档简介
课件26张PPT。 随机数的产生 对随机系统进行模拟,需要产生服从某种分
布的一系列随机数. ?定义 设随机变量X(总体)服从某种随机分布,对其进行了n次独立观察,得到一组简单随机样本 X1,X2,…,Xn ,满足1) X1,X2,…,Xn相互独立;2)每一个X1,X2,…,Xn都与总体X 同分布. 利用某种方法得到一串数列r1 , r2 , … , rn一.随机数的概念 在一定的统计意义下可作为随机样本
X1,X2,…,Xn
的一组样本值,称r1 , r2 , … , rn一组具有与X相同分布的随机数. 例1 设随机变量X~B(1, 0.5), 模拟该随机变
量X的一组样本值. 一种简单的方法是 抛一枚均匀硬币,观察出现正反面的情况,
出现正面记为数值“1”,否则记为“0”得:
0,0,1,0,1,1,1,0,1,0,0,0,
0,1,1,0,1,0, … 可看成总体X 的一系列样本值,或称产生了
一系列具有两点分布的随机数. 需要寻求一种简便、经济、可靠, 并能在计算机上实现的产生随机数的方法.数学软件有产生常用分布随机数的功能对特殊分布需要数据量很大时 不太有效二.均匀分布随机数的产生最常用、最基础的随
机数是在(0,1)区间
内均匀分布的随机数
(简记为RND) 理解为:随机变量X~U(0,1)的一组样本值的模拟值 一般采用某种数值计算方法产生随机数序列,在计算机上运算来得到.通常是利用递推公式:乘同余法混合同余法常用方法具有较好的
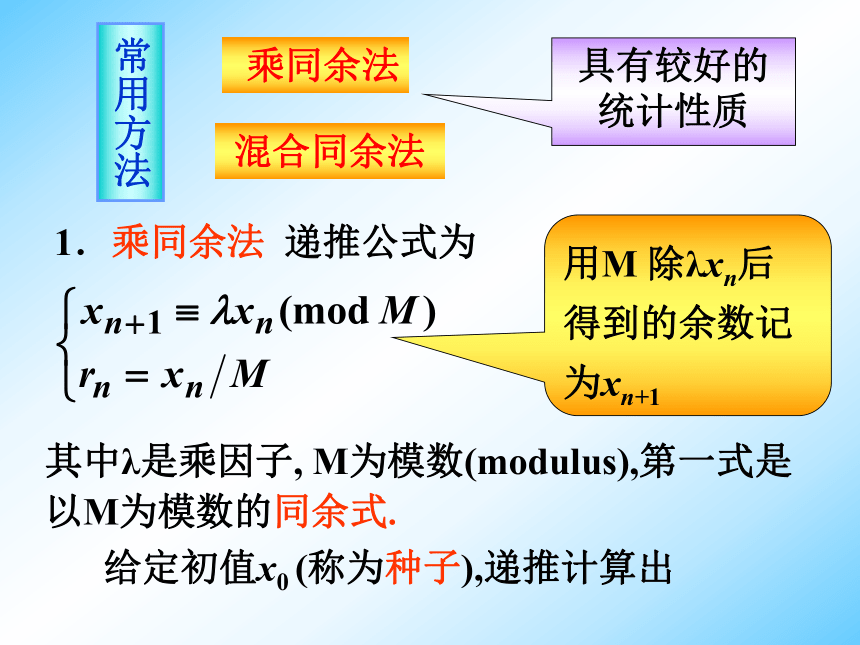
统计性质 1.乘同余法 递推公式为用M 除λxn后得到的余数记为xn+1其中λ是乘因子, M为模数(modulus),第一式是以M为模数的同余式.给定初值x0 (称为种子),递推计算出 r1,r2,…,
即在(0, 1)上均匀分布的随机数序列.例2 取x0=1,λ=7,M=103,有λx0=7×1=7 , x1=7 , r1=7/1000=0.007λx1=7×7=49 , x2=49 , r2=49/1000=0.049λx2=7×49=343 , x3=343 ,r3=343/1000=0.343λx3=7×343=2401 , x4=401 , r4=401/1000=0.401λx4=7×401=2807, x5=807 , r5=807/1000=0.807其余类推. 2.混合同余法 递推公式为用模 M 去除
λxn+C的余数其中,C是非负整数. 例3 :选λ=97,C=3,M=1000,得递推公式取定种子x0=71,得97x0+3=6890, x1=890, r1=0.89097x1+3=86333, x2=333, r2=0.33397x2+3=32304, x3=304, r3=0.30497x3+3=29491, x4=491, r4=0.49197x4+3=47830, x5=630, r5=0.630 余类推,接下来的随机数是:
0.113,0.964,0.511,0.570,0.293,0.424,
0.131,0.710,0.873,0.684,0.351,0.050,
0.853…有下述问题:1.数列{rn}是有周期的,周期L≤M(模数); 2. 数列{rn}本质上是实数列, 给定初始值由递推
公式计算出的一串确定的数列.不能简单等同于真正意义的随机数.解决方法与思路:1. 选择模拟参数2. 对数列进行统计检验 从计算机中直接调用
某种分布的随机数同样存在类似问题. x。=1,λ=513,M=236 (L=234≈2×1010)1) 周期的长度取决于参数x0, 入, M的选择; 2) 通过适当选取参数可以改善随机数的统计
性质. 几组供参考的参数值: x。=1,λ=7,M=1010 (L=5×107)1. 选择模拟参数 在计算机上编程产生随机数还应注意
浮点运算对周期的影响x。=1,λ=517,M=212 (L=240≈1012)2. 对数列进行统计检验 无论用哪一种方法产生的随机数序列 (实数列) RND, 都存在问题: 能否将其看着是在(0,1)上均匀分布的连续型随机变量X 的独立样本值? 对应的样本是否可以看成X的简单随机样本:1)X1,X2,…,Xn相互独立; 2)Xi ~U(0, 1) , (i=1, 2,…,n) 需判断是否具有较好的统计性质:独立性 均匀性进行统计检验 三. 任意分布随机数的模拟l.离散型随机数的模拟 设随机变量X 的分布律为 将{P( n)}作为区间(0, 1)的分点:P(0)P(1)P(2)P(3)01…… 若随机变量 R~U(0,1),有产生X的随机数的算法步骤 :(1) 产生一个(0, 1)区间上均匀分布随机数r(RND); (2) 若 P(n-1)<r≤P(n) ,则令X 取值为xn.例3 离散型随机变量X的分布律如下 设r1,r2,…,rN是RND随机数,令x1,x2,…,xN 即具有X 的分布律的随机数. 从理论上讲, 已解决了产生具有任何离散型分布的随机数的问题. 具体执行仍有困难,如X的取值是无穷多个的
情况. 可利用分布的自身特点,采用其他的模拟方法. 例4 随机变量X~B(n,p),其分布律为 随机变量X是 n 次独立贝努里试验中, 事件A发生的总次数, 其中p=P(A). 在计算机上模拟 n 重贝
努里试验来产生二项分布
的随机数. 当p 较大而计算精度要求较高时 2)统计ri (i=1,2,…,n)中使得 重复循环得到: n1,n2,…,nk即所求随机数列.练习题:
(1)生成100个服从B(20,0.3)的随机数
(2) 如何模拟参数为λ的泊松分布随机数?ri≤ p的个数ni. .算法步骤: 1)产生n个RND r1,r2,…,rn; 2.连续型随机数的模拟 利用在(0 , 1) 区间上均匀分布的随机数来模拟具有给定分布的连续型随机数. 两种方法反函数法 舍选法 1) 反函数法 设连续型随机变量Y的概率函数为 f(x), 需产生给定分布的随机数. 算法:1)产生n个RND 随机数r1,r2,…,rn; 所得yi, i=1,2, …,n 即所求.基本原理:
设随机变量Y的分布函数F(y)是连续函数,而且随机变量X~U(0,1),令Z=F-1(X)。
则Z与Y有相同分布. 例5 模拟服从参数为λ的指数分布的随机数,其概率密度函数为 若随机变量) X~U(0, 1)1-X ~U(0, 1)(1-ri)与ri 均为RND 随机数 模拟公式可改写为问题:请考虑如何利用此公式模拟泊松流?优点:一种普通而适用的方法; 缺点:当反函数不存在或难以求出时, 不宜于使 用.练习:生成100服从参数为10的指数分布的随机数。2)舍选法 基本思想:实质上是从许多RND随机数中选
出一部分, 使之成为具有给定分布的随机数.算法步骤: (1) 选取常数λ,使λf(x)<1,x∈(a, b); (2) 产生两个RND 随机数r1 、r2,令 y= a+(b-a)ri ; (3) 若 r2≤λf(y),则令x=y, 设随机变量X的概率密度函数为f(x),存在
实数 a分布由概率函数 f(x) 确定.舍选法算法原理分析:
设P{a<Z<b}=1,Z的概率密度为f(z),
选常数λ,使λf(z)≤1,z∈(a,b);
随机变量X1,X2相互独立Xi~U(0, 1),令 Y1=a+(b-a)X1~U(a, b);
若X2≤λf(Y1),则令 X = Y1,否则剔除X1,X2重复到(2)。
则随机变量X的分布与Z相同。注可选取有限区间(a1, b1),使得 ε是很小的正数.例如取 a1=μ-3σ,b1=μ+3σ,有 3.正态随机数的模拟产生正态分布
随机数的方法反函数法舍选法坐标变换法 中心极限定理1)坐标变换法设r1,r2 是RND随机数,令则 x1, x2是相互独立的标准正态分布的随机数. 练习:用舍选取法生成100个服从以期望μ=20,标准差σ=10的正态分布的随机数。 2)利用中心极限定理 产生服从N(μ,σ2)的算法步骤: 产生n 个RND 随机数:r1,r2,…,rn, 一般 n≥10若取n=12,简化为计算 x 是服从标准正态分布的随机数(3) 计算 y=σx+μ. y 是服从 N(μ,σ2) 分布的随机数.原理分析 设ζ1,ζ2,…,ζn是n个相互独立的随机变量,且ζi~U(0,1), i= 1,2, …,n,由中心极限定理知 渐近服从正态分布N(0, l ).
布的一系列随机数. ?定义 设随机变量X(总体)服从某种随机分布,对其进行了n次独立观察,得到一组简单随机样本 X1,X2,…,Xn ,满足1) X1,X2,…,Xn相互独立;2)每一个X1,X2,…,Xn都与总体X 同分布. 利用某种方法得到一串数列r1 , r2 , … , rn一.随机数的概念 在一定的统计意义下可作为随机样本
X1,X2,…,Xn
的一组样本值,称r1 , r2 , … , rn一组具有与X相同分布的随机数. 例1 设随机变量X~B(1, 0.5), 模拟该随机变
量X的一组样本值. 一种简单的方法是 抛一枚均匀硬币,观察出现正反面的情况,
出现正面记为数值“1”,否则记为“0”得:
0,0,1,0,1,1,1,0,1,0,0,0,
0,1,1,0,1,0, … 可看成总体X 的一系列样本值,或称产生了
一系列具有两点分布的随机数. 需要寻求一种简便、经济、可靠, 并能在计算机上实现的产生随机数的方法.数学软件有产生常用分布随机数的功能对特殊分布需要数据量很大时 不太有效二.均匀分布随机数的产生最常用、最基础的随
机数是在(0,1)区间
内均匀分布的随机数
(简记为RND) 理解为:随机变量X~U(0,1)的一组样本值的模拟值 一般采用某种数值计算方法产生随机数序列,在计算机上运算来得到.通常是利用递推公式:乘同余法混合同余法常用方法具有较好的
统计性质 1.乘同余法 递推公式为用M 除λxn后得到的余数记为xn+1其中λ是乘因子, M为模数(modulus),第一式是以M为模数的同余式.给定初值x0 (称为种子),递推计算出 r1,r2,…,
即在(0, 1)上均匀分布的随机数序列.例2 取x0=1,λ=7,M=103,有λx0=7×1=7 , x1=7 , r1=7/1000=0.007λx1=7×7=49 , x2=49 , r2=49/1000=0.049λx2=7×49=343 , x3=343 ,r3=343/1000=0.343λx3=7×343=2401 , x4=401 , r4=401/1000=0.401λx4=7×401=2807, x5=807 , r5=807/1000=0.807其余类推. 2.混合同余法 递推公式为用模 M 去除
λxn+C的余数其中,C是非负整数. 例3 :选λ=97,C=3,M=1000,得递推公式取定种子x0=71,得97x0+3=6890, x1=890, r1=0.89097x1+3=86333, x2=333, r2=0.33397x2+3=32304, x3=304, r3=0.30497x3+3=29491, x4=491, r4=0.49197x4+3=47830, x5=630, r5=0.630 余类推,接下来的随机数是:
0.113,0.964,0.511,0.570,0.293,0.424,
0.131,0.710,0.873,0.684,0.351,0.050,
0.853…有下述问题:1.数列{rn}是有周期的,周期L≤M(模数); 2. 数列{rn}本质上是实数列, 给定初始值由递推
公式计算出的一串确定的数列.不能简单等同于真正意义的随机数.解决方法与思路:1. 选择模拟参数2. 对数列进行统计检验 从计算机中直接调用
某种分布的随机数同样存在类似问题. x。=1,λ=513,M=236 (L=234≈2×1010)1) 周期的长度取决于参数x0, 入, M的选择; 2) 通过适当选取参数可以改善随机数的统计
性质. 几组供参考的参数值: x。=1,λ=7,M=1010 (L=5×107)1. 选择模拟参数 在计算机上编程产生随机数还应注意
浮点运算对周期的影响x。=1,λ=517,M=212 (L=240≈1012)2. 对数列进行统计检验 无论用哪一种方法产生的随机数序列 (实数列) RND, 都存在问题: 能否将其看着是在(0,1)上均匀分布的连续型随机变量X 的独立样本值? 对应的样本是否可以看成X的简单随机样本:1)X1,X2,…,Xn相互独立; 2)Xi ~U(0, 1) , (i=1, 2,…,n) 需判断是否具有较好的统计性质:独立性 均匀性进行统计检验 三. 任意分布随机数的模拟l.离散型随机数的模拟 设随机变量X 的分布律为 将{P( n)}作为区间(0, 1)的分点:P(0)P(1)P(2)P(3)01…… 若随机变量 R~U(0,1),有产生X的随机数的算法步骤 :(1) 产生一个(0, 1)区间上均匀分布随机数r(RND); (2) 若 P(n-1)<r≤P(n) ,则令X 取值为xn.例3 离散型随机变量X的分布律如下 设r1,r2,…,rN是RND随机数,令x1,x2,…,xN 即具有X 的分布律的随机数. 从理论上讲, 已解决了产生具有任何离散型分布的随机数的问题. 具体执行仍有困难,如X的取值是无穷多个的
情况. 可利用分布的自身特点,采用其他的模拟方法. 例4 随机变量X~B(n,p),其分布律为 随机变量X是 n 次独立贝努里试验中, 事件A发生的总次数, 其中p=P(A). 在计算机上模拟 n 重贝
努里试验来产生二项分布
的随机数. 当p 较大而计算精度要求较高时 2)统计ri (i=1,2,…,n)中使得 重复循环得到: n1,n2,…,nk即所求随机数列.练习题:
(1)生成100个服从B(20,0.3)的随机数
(2) 如何模拟参数为λ的泊松分布随机数?ri≤ p的个数ni. .算法步骤: 1)产生n个RND r1,r2,…,rn; 2.连续型随机数的模拟 利用在(0 , 1) 区间上均匀分布的随机数来模拟具有给定分布的连续型随机数. 两种方法反函数法 舍选法 1) 反函数法 设连续型随机变量Y的概率函数为 f(x), 需产生给定分布的随机数. 算法:1)产生n个RND 随机数r1,r2,…,rn; 所得yi, i=1,2, …,n 即所求.基本原理:
设随机变量Y的分布函数F(y)是连续函数,而且随机变量X~U(0,1),令Z=F-1(X)。
则Z与Y有相同分布. 例5 模拟服从参数为λ的指数分布的随机数,其概率密度函数为 若随机变量) X~U(0, 1)1-X ~U(0, 1)(1-ri)与ri 均为RND 随机数 模拟公式可改写为问题:请考虑如何利用此公式模拟泊松流?优点:一种普通而适用的方法; 缺点:当反函数不存在或难以求出时, 不宜于使 用.练习:生成100服从参数为10的指数分布的随机数。2)舍选法 基本思想:实质上是从许多RND随机数中选
出一部分, 使之成为具有给定分布的随机数.算法步骤: (1) 选取常数λ,使λf(x)<1,x∈(a, b); (2) 产生两个RND 随机数r1 、r2,令 y= a+(b-a)ri ; (3) 若 r2≤λf(y),则令x=y, 设随机变量X的概率密度函数为f(x),存在
实数 a
设P{a<Z<b}=1,Z的概率密度为f(z),
选常数λ,使λf(z)≤1,z∈(a,b);
随机变量X1,X2相互独立Xi~U(0, 1),令 Y1=a+(b-a)X1~U(a, b);
若X2≤λf(Y1),则令 X = Y1,否则剔除X1,X2重复到(2)。
则随机变量X的分布与Z相同。注可选取有限区间(a1, b1),使得 ε是很小的正数.例如取 a1=μ-3σ,b1=μ+3σ,有 3.正态随机数的模拟产生正态分布
随机数的方法反函数法舍选法坐标变换法 中心极限定理1)坐标变换法设r1,r2 是RND随机数,令则 x1, x2是相互独立的标准正态分布的随机数. 练习:用舍选取法生成100个服从以期望μ=20,标准差σ=10的正态分布的随机数。 2)利用中心极限定理 产生服从N(μ,σ2)的算法步骤: 产生n 个RND 随机数:r1,r2,…,rn, 一般 n≥10若取n=12,简化为计算 x 是服从标准正态分布的随机数(3) 计算 y=σx+μ. y 是服从 N(μ,σ2) 分布的随机数.原理分析 设ζ1,ζ2,…,ζn是n个相互独立的随机变量,且ζi~U(0,1), i= 1,2, …,n,由中心极限定理知 渐近服从正态分布N(0, l ).
