北师大版九年级上册第六章反比例函数复习课件(21张PPT)
文档属性
| 名称 | 北师大版九年级上册第六章反比例函数复习课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 695.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-17 00:00:00 | ||
图片预览





文档简介
课件21张PPT。反比例函数复习考纲要求1.概念(1)认识反比例函数
(2)求 解析式:待定系数法
2.图像:双曲线
3.性质:(1)位置
(2)对称性.
(3)增减性.
(4) K的几何意义
4.综合应用:数形结合解决实际问题四大视角看函数1、反比例函数:
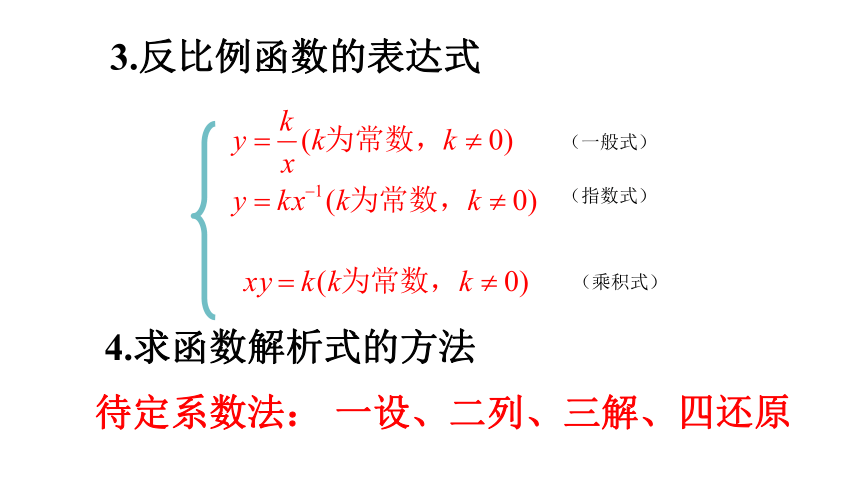
一般地,如果两个变量x,y之间的关系可以表示成:的形式,那么称y是x的反比例函数2 、反比例函数的自变量x,因变量y的取值范围:(x≠0 ,y≠0)反比例函数的概念3.反比例函数的表达式4.求函数解析式的方法待定系数法: 一设、二列、三解、四还原基础知识过关之一1.下列函数中,y是x的反比例函数的是( )
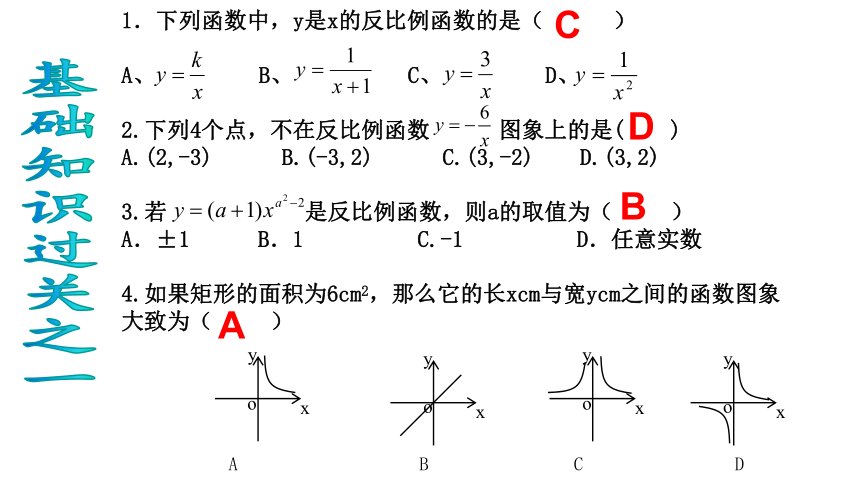
A、 B、 C、 D、
2.下列4个点,不在反比例函数 图象上的是( )
A.(2,-3) B.(-3,2) C.(3,-2) D.(3,2)
3.若 是反比例函数,则a的取值为( )
A.±1 B.1 C.-1 D.任意实数
4.如果矩形的面积为6cm2,那么它的长xcm与宽ycm之间的函数图象
大致为( ) CDBA当k>0时,y随x的增大而减小
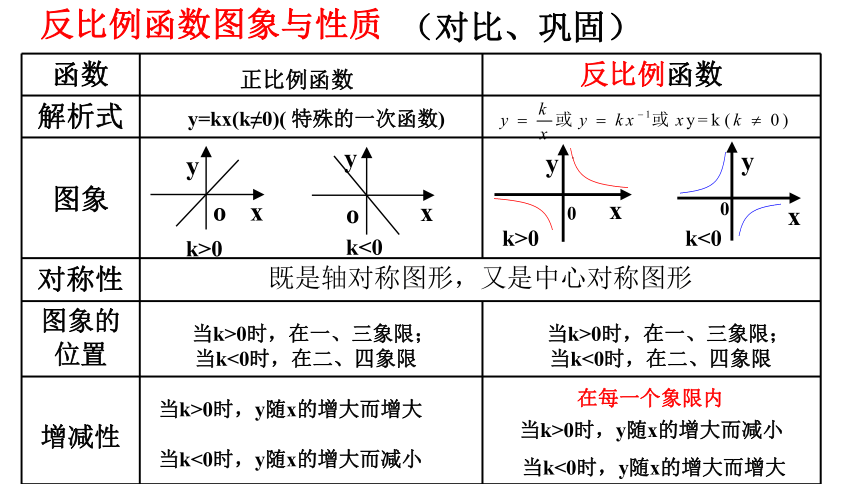
当k<0时,y随x的增大而增大反比例函数图象与性质y=kx(k≠0)( 特殊的一次函数) 当k>0时,在一、三象限;
当k<0时,在二、四象限当k>0时,y随x的增大而增大
当k<0时,y随x的增大而减小在每一个象限内 当k>0时,在一、三象限;
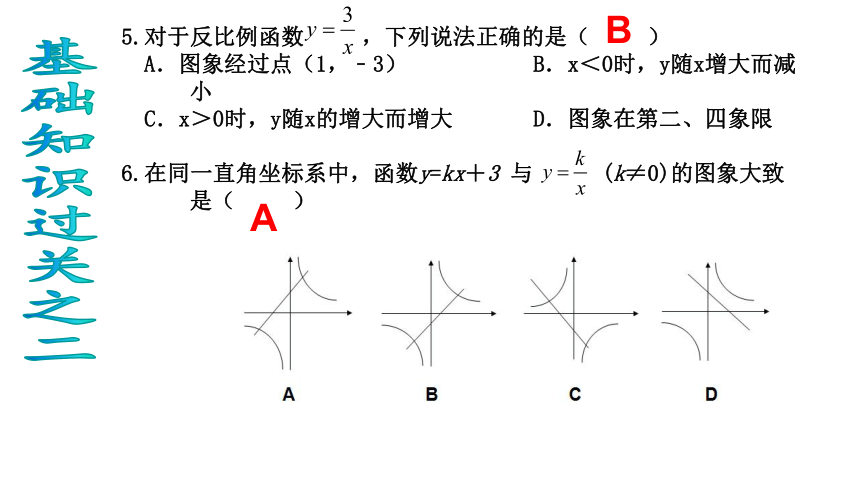
当k<0时,在二、四象限正比例函数 (对比、巩固)5.对于反比例函数 ,下列说法正确的是( )
A.图象经过点(1,﹣3) B.x<0时,y随x增大而减小
C.x>0时,y随x的增大而增大 D.图象在第二、四象限
6.在同一直角坐标系中,函数y=kx+3 与 (k≠0)的图象大致是( )
BA基础知识过关之二 已知点A(1,y1),B(2,y2 ),都在反比例函数 的图象上,
则___<___ (填y1 , y2 ).
变式2:在反比例函数 的图象上有两点A(x1, y1 ),B(x2 ,y2 ),
当x1<0< x2有y1 < y2 ,则k的取值范围是________.
变式1:已知反比例函数 ,若A(x1,y1),B(x2,y2 ),C(x3,y3)
是这个反比例函数图象上的三点,且 ,
则___<___ <___ (填y1 , y2,y3 ).k的几何意义:(x,y)(x,y)B
7.如上右图 ,A、C是函数的图象上的任意两点,过A作轴的垂
线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为
S1,RtΔCOD的面积为S2,则 ( )
A.S1 >S2 B. S1
C.S1=S2 D. S1与S2的大小关系不能确定C基础知识过关之三ByxQAQO?像这样的图形变换叫等积变换考点三:K的几何意义D请注意:不要忽略k的符号A. 6 B. -6
C.-3 D. 3综合应用题型一:反比例与三角形全等CD解: 过M作CD∥x轴,过B作BD⊥CD 易得△ACD≌△MDBA、B两点坐标分别为(0,-1),(5,0)设M坐标为(x,y),设CM=x,CO=BD=y由全等可知 AC=1+y=MD=5-x
CM=x=BD=y
解得x=y=2 ,即M坐标为(2,2),
∴ k=4
综合应用题型二:反比例与三角形相似10.已知直线 与双曲线 交于点A,将直线 向右平移4.5个单位后,与双曲线交于点B,与x轴交于点C,若 ,求k的值?
.解:作AC⊥x轴,BE⊥x轴
ED易得△ADO∽△BCE 且相似比为2 直线平移后可得C坐标为(4.5,0)解得x=3 A的坐标为(3,4)∴K=12综合应用题型三:反比例与图形变换11.如图,直线y=???12?x+1分别交x、y轴分别于A、B,
将线段AB绕点M旋转180°得线段CD,双曲线
?恰好过C、D、M三点,求k的值?. 解:由已知可得A、B两点坐标分别为(2,0)和(0,1)设M坐标为(a,b),M为AC、BD中点
可得C、D坐标分别为(2a-2,b)(2a,2b-1)∵M、C、D三点都在双曲线上
∴ab=k ,(2a-2)b=k ,2a(2b-1)=k
. 如图,反比例函数 的图像与一次函数 的图像
分别 交于M、N 两点,已知点M(-2,m),
求:(1)求反比例函数的表达式;
(2)直接写出不等式 的解集
. 综合应用题型四:反比例与一次函数解: (1)∵点M(-2,m)在一次函数图像上,
∴M(-2,1). ∵反比例函数的图象经过点M(-2,1),
∴k=-2×1=-2∴反比例函数的表达式为 12 . 如图,反比例函数 的图像与一次函数 的图像
分别 交于M、N 两点,已知点M(-2,m),
综合应用题型四:反比例与一次函数 求:(1)求反比例函数的表达式;
(2)直接写出不等式 的解集
. 解:(2) 根据对称性可知N坐标为(2,-1)结合图像可知 的解集为-2<x<0,和 x>2 12. 如图,反比例函数 的图像与一次函数 的图像
分别 交于M、N 两点,已知点M(-2,m),
综合应用题型四:反比例与一次函数 求:(3)点P为y轴上的一点,当∠MPN为直角 时,写出点P的坐标课堂小结1、反比例函数的定义(三种表达式)2、反比例函数的图象与性质3、反比例函数的综合应用作业布置第6章复习作业谢 谢
(2)求 解析式:待定系数法
2.图像:双曲线
3.性质:(1)位置
(2)对称性.
(3)增减性.
(4) K的几何意义
4.综合应用:数形结合解决实际问题四大视角看函数1、反比例函数:
一般地,如果两个变量x,y之间的关系可以表示成:的形式,那么称y是x的反比例函数2 、反比例函数的自变量x,因变量y的取值范围:(x≠0 ,y≠0)反比例函数的概念3.反比例函数的表达式4.求函数解析式的方法待定系数法: 一设、二列、三解、四还原基础知识过关之一1.下列函数中,y是x的反比例函数的是( )
A、 B、 C、 D、
2.下列4个点,不在反比例函数 图象上的是( )
A.(2,-3) B.(-3,2) C.(3,-2) D.(3,2)
3.若 是反比例函数,则a的取值为( )
A.±1 B.1 C.-1 D.任意实数
4.如果矩形的面积为6cm2,那么它的长xcm与宽ycm之间的函数图象
大致为( ) CDBA当k>0时,y随x的增大而减小
当k<0时,y随x的增大而增大反比例函数图象与性质y=kx(k≠0)( 特殊的一次函数) 当k>0时,在一、三象限;
当k<0时,在二、四象限当k>0时,y随x的增大而增大
当k<0时,y随x的增大而减小在每一个象限内 当k>0时,在一、三象限;
当k<0时,在二、四象限正比例函数 (对比、巩固)5.对于反比例函数 ,下列说法正确的是( )
A.图象经过点(1,﹣3) B.x<0时,y随x增大而减小
C.x>0时,y随x的增大而增大 D.图象在第二、四象限
6.在同一直角坐标系中,函数y=kx+3 与 (k≠0)的图象大致是( )
BA基础知识过关之二 已知点A(1,y1),B(2,y2 ),都在反比例函数 的图象上,
则___<___ (填y1 , y2 ).
变式2:在反比例函数 的图象上有两点A(x1, y1 ),B(x2 ,y2 ),
当x1<0< x2有y1 < y2 ,则k的取值范围是________.
变式1:已知反比例函数 ,若A(x1,y1),B(x2,y2 ),C(x3,y3)
是这个反比例函数图象上的三点,且 ,
则___<___ <___ (填y1 , y2,y3 ).k的几何意义:(x,y)(x,y)B
7.如上右图 ,A、C是函数的图象上的任意两点,过A作轴的垂
线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为
S1,RtΔCOD的面积为S2,则 ( )
A.S1 >S2 B. S1
C.S1=S2 D. S1与S2的大小关系不能确定C基础知识过关之三ByxQAQO?像这样的图形变换叫等积变换考点三:K的几何意义D请注意:不要忽略k的符号A. 6 B. -6
C.-3 D. 3综合应用题型一:反比例与三角形全等CD解: 过M作CD∥x轴,过B作BD⊥CD 易得△ACD≌△MDBA、B两点坐标分别为(0,-1),(5,0)设M坐标为(x,y),设CM=x,CO=BD=y由全等可知 AC=1+y=MD=5-x
CM=x=BD=y
解得x=y=2 ,即M坐标为(2,2),
∴ k=4
综合应用题型二:反比例与三角形相似10.已知直线 与双曲线 交于点A,将直线 向右平移4.5个单位后,与双曲线交于点B,与x轴交于点C,若 ,求k的值?
.解:作AC⊥x轴,BE⊥x轴
ED易得△ADO∽△BCE 且相似比为2 直线平移后可得C坐标为(4.5,0)解得x=3 A的坐标为(3,4)∴K=12综合应用题型三:反比例与图形变换11.如图,直线y=???12?x+1分别交x、y轴分别于A、B,
将线段AB绕点M旋转180°得线段CD,双曲线
?恰好过C、D、M三点,求k的值?. 解:由已知可得A、B两点坐标分别为(2,0)和(0,1)设M坐标为(a,b),M为AC、BD中点
可得C、D坐标分别为(2a-2,b)(2a,2b-1)∵M、C、D三点都在双曲线上
∴ab=k ,(2a-2)b=k ,2a(2b-1)=k
. 如图,反比例函数 的图像与一次函数 的图像
分别 交于M、N 两点,已知点M(-2,m),
求:(1)求反比例函数的表达式;
(2)直接写出不等式 的解集
. 综合应用题型四:反比例与一次函数解: (1)∵点M(-2,m)在一次函数图像上,
∴M(-2,1). ∵反比例函数的图象经过点M(-2,1),
∴k=-2×1=-2∴反比例函数的表达式为 12 . 如图,反比例函数 的图像与一次函数 的图像
分别 交于M、N 两点,已知点M(-2,m),
综合应用题型四:反比例与一次函数 求:(1)求反比例函数的表达式;
(2)直接写出不等式 的解集
. 解:(2) 根据对称性可知N坐标为(2,-1)结合图像可知 的解集为-2<x<0,和 x>2 12. 如图,反比例函数 的图像与一次函数 的图像
分别 交于M、N 两点,已知点M(-2,m),
综合应用题型四:反比例与一次函数 求:(3)点P为y轴上的一点,当∠MPN为直角 时,写出点P的坐标课堂小结1、反比例函数的定义(三种表达式)2、反比例函数的图象与性质3、反比例函数的综合应用作业布置第6章复习作业谢 谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
