2.1.2 指数函数及其性质(3) 同步练习 含答案
文档属性
| 名称 | 2.1.2 指数函数及其性质(3) 同步练习 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 998.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.1.2指数函数及其性质(3)
一、选择题
已知集合A={x|x2-2x-3<0},集合B={x|2x+1>1},则?BA=( )
A. [3,+∞) B. (3,+∞)
C. (-∞,-1]∪[3,+∞) D. (-∞,-1)∪(3,+∞)
函数f(x)=-3|x|+1的图象大致是( )
A. B. C. D.
函数的值域是( )
[0,+∞) B. [0,2] C. [0,2) D. (0,2)
已知函数f(x)=4+ax-1(a>0且a≠1)的图象恒过定点P,则定点P的坐标是( )
A. (4,0) B. (1,4) C. (0,4) D. (1,5)
若不等式恒成立,则实数a的取值范围是( )
A. (0,1) B. C. D.
二次函数y=-x2-4x(x>-2)与指数函数的交点个数有( )
A. 3个 B. 2个 C. 1个 D. 0个
已知实数a>b,则下列结论正确的是
A. B. a2>b2 C. D. 2a>2b
若函数单调递增,则实数的取值范围是( )
A. B. C. D. (2,3)
二、填空题
9.不等式的解集为________
10.已知函数,若方程有3个不等的实根,则实数m的取值范围是___
三、解答题
11.已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2)
(1)求g(x)的解析式及定义域;
(2)若x∈[0,1],求函数g(x)的最大值和最小值.
答案和解析
1.A
解:A={x|x2-2x-3<0}={x|-1<x<3},B={x|2x+1>1}={x|x>-1},?BA=[3,+∞).
2.A
解:∵函数f(x)=-3|x|+1 ∴f(-x)=-3|-x|+1=-3|x|+1=f(x), 即函数为偶函数,其图象关于y轴对称,故排除BD 当x=0时,f(0)=-30+1=0,即函数图象过原点,故排除C
3.C 解:∵函数的值域, ∴4-2x≥0,∴x≤2 当x=2时,y=0,∵0≤4-2x<4, ∴0≤y<2, ∴函数的值域为:[0,2),
4.D
5.B
解:不等式恒成立,即<恒成立,即x2-2ax>-(3x+a2)恒成立,即x2-(2a-3)x+a2>0恒成立,∴△=(2a-3)2-4a2<0,即(2a-3+2a)(2a-3-2a)<0,解得a>,
6.C
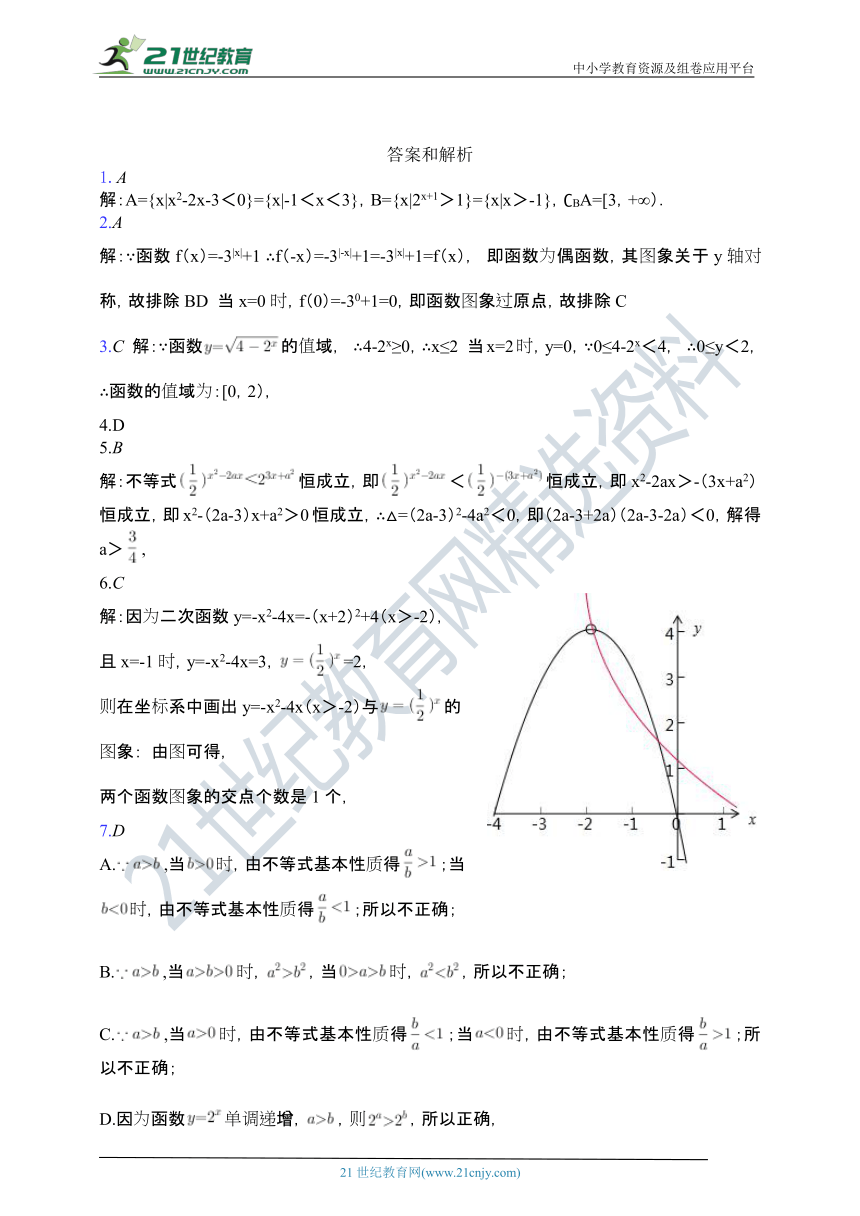
解:因为二次函数y=-x2-4x=-(x+2)2+4(x>-2),
且x=-1时,y=-x2-4x=3,=2,
则在坐标系中画出y=-x2-4x(x>-2)与的图象: 由图可得,
两个函数图象的交点个数是1个,
7.D
A.,当时,由不等式基本性质得;当时,由不等式基本性质得;所以不正确;
B.,当时,,当时,,所以不正确;
C.,当时,由不等式基本性质得;当时,由不等式基本性质得;所以不正确;
D.因为函数单调递增,,则,所以正确,
8.B
解:∵函数单调递增,由指数函数以及一次函数的单调性的性质,可得3-a>0且a>1.但应当注意两段函数在衔接点x=7处的函数值大小的比较,即(3-a)×7-3≤a,可以解得a≥,综上,实数a的取值范围是[,3).
9
10. 如图
11.解:(1)g(x)=f(2x)-f(x+2)=22x-2x+2,∵f(x)=2x的定义域是[0,3],
∴,解得0≤x≤1,∴g(x)的定义域为[0,1].
(2)由(1)得g(x)=22x-2x+2,设2x=t,则t∈[1,2],∴g(t)=t2-4t,∴g(t)在[1,2]上单调递减,∴g(t)max=g(1)=-3,g(t)min=g(2)=-4.∴函数g(x)的最大值为-3,最小值为-4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.1.2指数函数及其性质(3)
一、选择题
已知集合A={x|x2-2x-3<0},集合B={x|2x+1>1},则?BA=( )
A. [3,+∞) B. (3,+∞)
C. (-∞,-1]∪[3,+∞) D. (-∞,-1)∪(3,+∞)
函数f(x)=-3|x|+1的图象大致是( )
A. B. C. D.
函数的值域是( )
[0,+∞) B. [0,2] C. [0,2) D. (0,2)
已知函数f(x)=4+ax-1(a>0且a≠1)的图象恒过定点P,则定点P的坐标是( )
A. (4,0) B. (1,4) C. (0,4) D. (1,5)
若不等式恒成立,则实数a的取值范围是( )
A. (0,1) B. C. D.
二次函数y=-x2-4x(x>-2)与指数函数的交点个数有( )
A. 3个 B. 2个 C. 1个 D. 0个
已知实数a>b,则下列结论正确的是
A. B. a2>b2 C. D. 2a>2b
若函数单调递增,则实数的取值范围是( )
A. B. C. D. (2,3)
二、填空题
9.不等式的解集为________
10.已知函数,若方程有3个不等的实根,则实数m的取值范围是___
三、解答题
11.已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2)
(1)求g(x)的解析式及定义域;
(2)若x∈[0,1],求函数g(x)的最大值和最小值.
答案和解析
1.A
解:A={x|x2-2x-3<0}={x|-1<x<3},B={x|2x+1>1}={x|x>-1},?BA=[3,+∞).
2.A
解:∵函数f(x)=-3|x|+1 ∴f(-x)=-3|-x|+1=-3|x|+1=f(x), 即函数为偶函数,其图象关于y轴对称,故排除BD 当x=0时,f(0)=-30+1=0,即函数图象过原点,故排除C
3.C 解:∵函数的值域, ∴4-2x≥0,∴x≤2 当x=2时,y=0,∵0≤4-2x<4, ∴0≤y<2, ∴函数的值域为:[0,2),
4.D
5.B
解:不等式恒成立,即<恒成立,即x2-2ax>-(3x+a2)恒成立,即x2-(2a-3)x+a2>0恒成立,∴△=(2a-3)2-4a2<0,即(2a-3+2a)(2a-3-2a)<0,解得a>,
6.C
解:因为二次函数y=-x2-4x=-(x+2)2+4(x>-2),
且x=-1时,y=-x2-4x=3,=2,
则在坐标系中画出y=-x2-4x(x>-2)与的图象: 由图可得,
两个函数图象的交点个数是1个,
7.D
A.,当时,由不等式基本性质得;当时,由不等式基本性质得;所以不正确;
B.,当时,,当时,,所以不正确;
C.,当时,由不等式基本性质得;当时,由不等式基本性质得;所以不正确;
D.因为函数单调递增,,则,所以正确,
8.B
解:∵函数单调递增,由指数函数以及一次函数的单调性的性质,可得3-a>0且a>1.但应当注意两段函数在衔接点x=7处的函数值大小的比较,即(3-a)×7-3≤a,可以解得a≥,综上,实数a的取值范围是[,3).
9
10. 如图
11.解:(1)g(x)=f(2x)-f(x+2)=22x-2x+2,∵f(x)=2x的定义域是[0,3],
∴,解得0≤x≤1,∴g(x)的定义域为[0,1].
(2)由(1)得g(x)=22x-2x+2,设2x=t,则t∈[1,2],∴g(t)=t2-4t,∴g(t)在[1,2]上单调递减,∴g(t)max=g(1)=-3,g(t)min=g(2)=-4.∴函数g(x)的最大值为-3,最小值为-4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
