高数选修2-1同步1对1复习课程10空间向量数量积运算(无答案)
文档属性
| 名称 | 高数选修2-1同步1对1复习课程10空间向量数量积运算(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 568.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-18 11:35:40 | ||
图片预览



文档简介
全方位教学辅导教案
学 科 数 学 任课老师 授课时间 ****年**月** 日 星期**[来源:学,科,网]
姓 名 性别 年级 高二 课次:第**次课
教 学 内 容 10空间向量及其运算2
考 点 难 点 空间向量的数量积空间向量的正交分解
知识点剖析和例题精讲
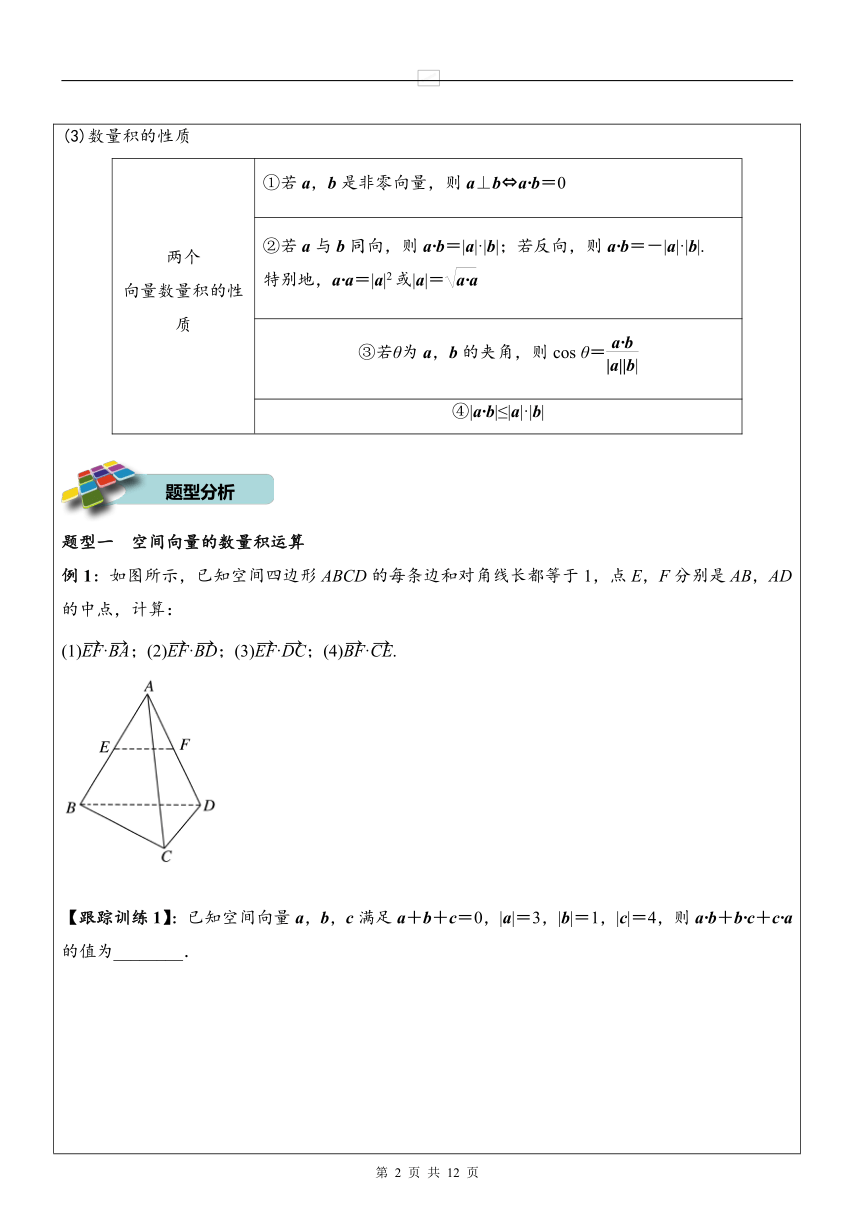
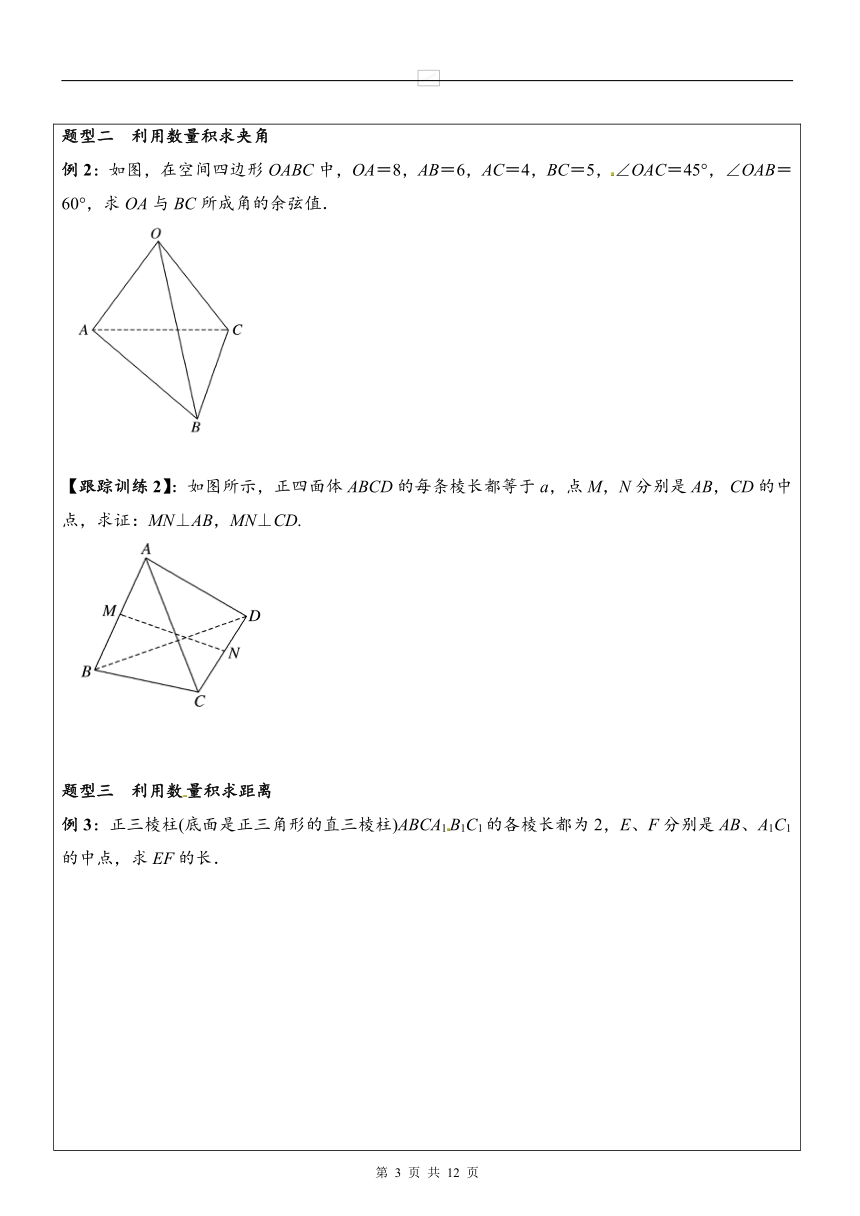
一、空间向量的数量积知识点一 空间向量的夹角定义已知两个非零向量a,b,在空间任取一点O,作=a,=b,则∠AOB叫做向量a,b的夹角 记法[来源:学*科*网Z*X*X*K]〈a,b〉 范围〈a,b〉∈[0,π].当〈a,b〉=时,a_⊥_b 知识点二 空间向量的数量积 (1)定义已知两个非零向量a,b,则则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.(2)数量积的运算律数乘向量与向量数量积的结合律(λa)·b=λ(a·b) 交换律a·b=b·a 分配律a·(b+c)=a·b+a·c (3)数量积的性质 两个 向量数量积的性质①若a,b是非零向量,则a⊥b?a·b=0 ②若a与b同向,则a·b=|a|·|b|;若反向,则a·b=-|a|·|b|. 特别地,a·a=|a|2或|a|= ③若θ为a,b的夹角,则cos θ= ④|a·b|≤|a|·|b| 题型一 空间向量的数量积运算 例1:如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算: (1)·;(2)·;(3)·;(4)·. 【跟踪训练1】:已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为________. 题型二 利用数量积求夹角 例2:如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值. 【跟踪训练2】:如图所示,正四面体ABCD的每条棱长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD. 题型三 利用数量积求距离 例3:正三棱柱(底面是正三角形的直三棱柱)ABCA1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长. 【跟踪训练3】如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长. 【课堂训练】1.若a,b均为非零向量,则a·b=|a||b|是a与b共线的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 2.已知a,b均为单位向量,它们的夹角为60°,那么|a-3b|等于( ) A. B. C. D.4 3.对于向量a、b、c和实数λ,下列命题中的真命题是( ) A.若a·b=0,则a=0或b=0 B.若λa=0,则λ=0或a=0 C.若a2=b2,则a=b或a=-b D.若a·b=a·c,则b=c 4.设向量a,b满足|a+b|=,|a-b|=,则a·b等于( ) A.1 B.2 C.3 D.5 5.若向量a,b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|等于( ) A.2 B. C.1 D. 一、选择题 1.下列命题中,不正确的有( ) ①=|a|;②m(λa)·b=(mλ)a·b;③a·(b+c)=(b+c)·a;④a2b=b2a. A.4个 B.3个 C.2个 D.1个 2.下列命题中正确的是( ) A.(a·b)2=a2·b2 B.|a·b|≤|a||b| C.(a·b)·c=a·(b·c) D.若a⊥(b-c),则a·b=a·c=0 3.空间四边形ABCD的各边和对角线均相等,E是BC的中点,那么( ) A.·<· B.·=· C.·>· D.·与·的大小不能比较 4.已知|a|=2,|b|=3,〈a,b〉=60°,则|2a-3b|等于( ) A. B.97 C. D.61 5.已知向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a-b)·a等于( ) A.12 B.8+ C.4 D.13 6.已知|a|=1,|b|=,且a-b与a垂直,则a与b的夹角为( ) A.60° B.30° C.135° D.45° 7.设A、B、C、D是空间不共面的四点,且满足·=0,·=0,·=0,则△BCD是( ) A.钝角三角形 B.锐角三角形 C.直角三角形 D.不确定 二、填空题 8.空间向量a,b之间的夹角为30°,且|a|=3,|b|=4,则a·b=________,a2=________,b2=________,(a+2b)·(a-b)=________. 9.在四面体OABC中,棱OA,OB,OC两两垂直,且OA=1,OB=2,OC=3,G为△ABC的重心,则·(++)=________. 10.已知|a|=3,|b|=4,m=a+b,n=a+λb,〈a,b〉=135°,且m⊥n,则实数λ等于________. 11.如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是________.三、解答题 12.已知正四面体OABC的棱长为1.求: (1)·; (2)(+)·(+); (3)|++|. 13.如图所示,在正方体ABCD-A1B1C1D1中,求异面直线A1B与AC所成的角. 二、空间向量的正交分解及其坐标表示知识点一 空间向量基本定理定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc. 其中{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量.知识点二 空间向量的正交分解及其坐标表示 (1)单位正交基底三个有公共起点O的两两垂直的单位向量e1,e2,e3称为单位正交基底.(2)空间直角坐标系以e1,e2,e3的公共起点O为原点,分别以e1,e2,e3的方向为x轴,y轴,z轴的正方向建立空间直角坐标系Oxyz.(3)空间向量的坐标表示对于空间任意一个向量p,一定可以把它平移,使它的起点与原点O重合,得到向量=p.由空间向量基本定理可知,存在有序实数组{x,y,z},使得p=xe1+ye2+ze3把x,y,z称作向量p在单位正交基底e1,e2,e3下的坐标,记作p=(x,y,z).题型一 空间向量的基底 例1:已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{,,}能否作为空间的一个基底. 【跟踪训练1】已知点O,A,B,C为空间不共面的四点,且向量a=++,向量b=+-,则与a,b不能构成空间基底的向量是( ) A. B. C. D.或题型二 用基底表示向量 例2:如图,四棱锥POABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,试用a,b,c表示,,,. 【跟踪训练2】如图所示,已知平行六面体ABCD-A1B1C1D1,设=a,=b,=c,P是CA1的中点,M是CD1的中点.用基底{a,b,c}表示以下向量:;(2). 题型三 空间向量的坐标表示 例3:已知PA垂直于正方形ABCD所在的平面,M、N分别是AB、PC的中点,并且PA=AD=1,建立适当坐标系,求向量的坐标. [来源:学科网ZXXK] 【跟踪训练3】已知PA垂直于正方形ABCD所在的平面,M、N分别是AB、PC的中点,并且PA=AD=1,建立适当坐标系,求向量、的坐标. 【课堂训练】[来源:Z&xx&k.Com]1.已知A(2,3-μ,-1+v)关于x轴的对称点是A′(λ,7,-6),则λ,μ,v的值为( ) A.λ=-2,μ=-4,v=-5 B.λ=2,μ=-4,v=-5 C.λ=-2,μ=10,v=8 D.λ=2,μ=10,v=7 2.与向量m=(0,1,-2)共线的向量是( ) A.(2,0,-4) B.(3,6,-12) C.(1,1,-2) D.(0,,-1) 3.已知向量a,b,c是空间的一个基底,下列向量中可以与p=2a-b,q=a+b构成空间的另一个基底的是________.(填序号) ①2a;②-b;③c;④a+c. 4.如图在边长为2的正方体ABCD-A1B1C1D1中,取D点为原点建立空间直角坐标系,O,M分别是AC,DD1的中点,写出下列向量的坐标.=________,=________. 5.如图,在梯形ABCD中,AB∥CD,AB=2CD,点O为空间任一点,设=a,=b,=c,则向量用a,b,c表示为________. 一、选择题 1.下列命题中正确的是( ) A.若a∥b,b∥c,则a∥c B.任意两个相等的非零向量的始点与终点是一个平行四边形的四个顶点 C.向量a与b不共线,则a与b都是非零向量 D.有相同起点的两个非零向量不平行 2.已知{a,b,c}是空间的一个基底,则可以与向量p=a+b,q=a-b构成基底的向量是( ) A.a B.b C.a+2b D.a+2c 3.在空间直角坐标系Oxyz中,下列说法正确的是( ) A.向量与点B的坐标相同 B.向量与点A的坐标相同 C.向量与向量的坐标相同 D.向量与向量-的坐标相同4.正方体ABCDA1B1C1D1的棱长为a,=,点N为B1B的中点,则||等于( ) A.a B.a C.a D.a [来源:Zxxk.Com]5.在以下三个命题中,真命题的个数是( ) ①三个非零向量a,b,c不能构成空间的一个基底,则a,b,c共面; ②若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a、b共线; ③若a,b是两个不共线的向量,而c=λa+μb(λ,μ∈R且λμ≠0),则{a,b,c}构成空间的一个基底. A.0 B.1 C.2 D.3 6.设向量a、b、c不共面,则下列集合可作为空间的一个基底的是( ) A.{a+b,b-a,a} B.{a+b,b-a,b} C.{a+b,b-a,c} D.{a+b+c,a+b,c} 7.在△ABC中,=c,=b,若点D满足=2,若将b与c作为基底,则等于( ) A.b+c B.c-b C.b-c D.b+c 二、填空题 8.已知A,B,C三点共线,则对空间任一点O,存在三个不为0的实数λ,m,n,使λ+m+n=0,那么λ+m+n的值为________. 9.已知在四面体ABCD中,=a-2c,=5a+6b-8c,对角线AC,BD的中点分别为点E,F,则=________.(用a,b,c表示) 10.在平行六面体ABCD-A1B1C1D1中,若=x+2y+3z,则x+y+z=________. 三、解答题11.平行六面体OABC O′A′B′C′,且=a,=b,=c. (1)用a,b,c表示向量; (2)设G,H分别是侧面BB′C′C和O′A′B′C′的中心,用a,b,c表示. 12.如图所示,在△ABO中,=,=,AD与BC相交于点M,设=a,=b.试用a和b表示向量.
知识点睛
题型分析
达标检测
知识点睛
题型分析
达标检测
