高数选修2-1同步1对1复习课程11空间向量坐标运算(无答案)
文档属性
| 名称 | 高数选修2-1同步1对1复习课程11空间向量坐标运算(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 341.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-18 11:34:59 | ||
图片预览



文档简介
全方位教学辅导教案
学 科 数 学 任课老师 授课时间 ****年**月** 日 星期**
姓 名 性别 年级 高二 课次:第**次课
教 学 内 容 11空间向量的坐标运算
考 点 难 点 空间向量的数量积空间向量的坐标运算
知识点剖析和例题精讲
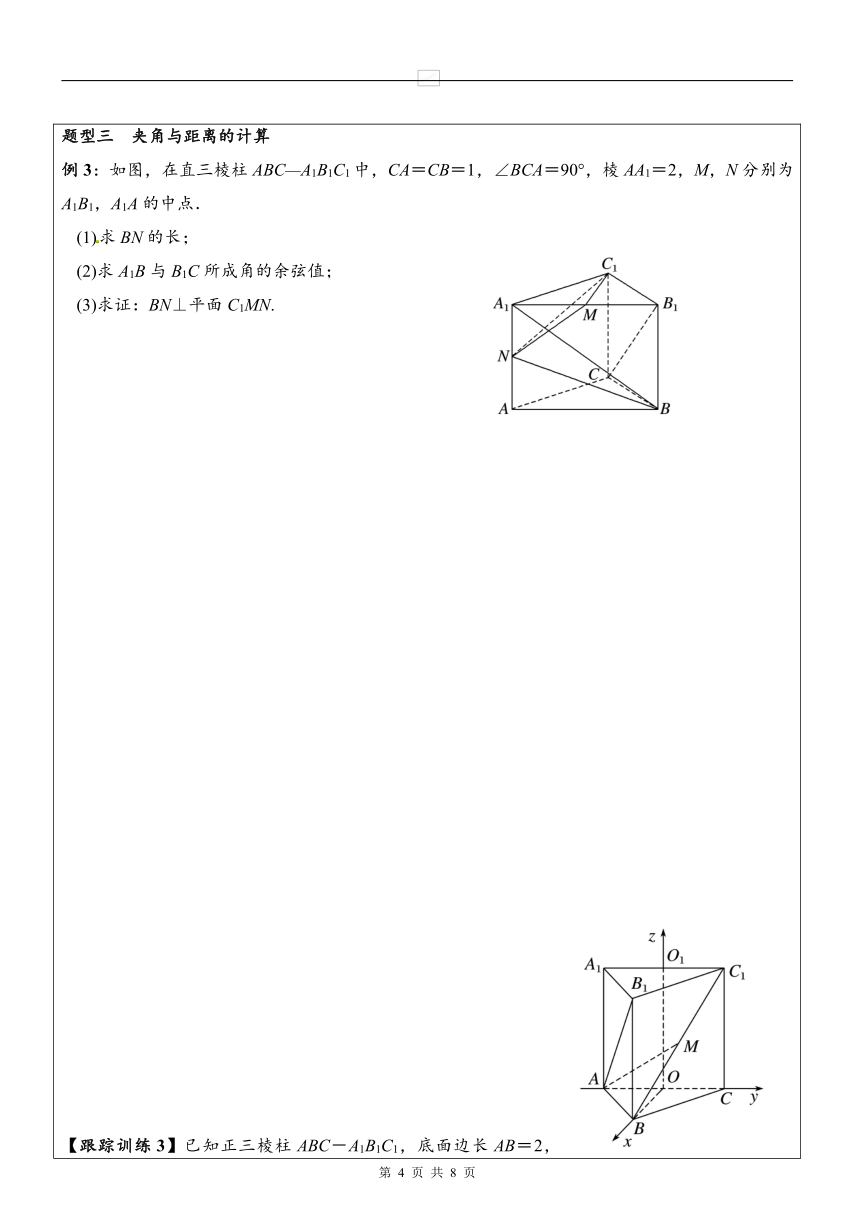
一、空间向量的坐标运算知识点一 空间向量的坐标运算设a=(a1,a2,a3),b=(b1,b2,b3),a+b=(a1+b1,a2+b2,a3+b3),a-b=(a1-b1,a2-b2,a3-b3),λa=(λa1,λa2,λa3),a·b=a1b1+a2b2+a3b3.知识点二 空间向量的平行、垂直及模、夹角设a=(a1,a2,a3),b=(b1,b2,b3), 则a∥b?a=λb?a1=λb1,a2=λb2,a3=λb3 (λ∈R);a⊥b?a·b=0?a1b1+a2b2+a3b3=0; |a|==; cos〈a,b〉==.知识点三 空间两点间的距离已知点A(a1,b1,c1),B(a2,b2,c2),则A,B两点间的距离dAB=||=.题型一 空间直角坐标系与空间向量的坐标表示 例1:设O为坐标原点,向量=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则当·取得最小值时,求点Q的坐标. [来源:学&科&网Z&X&X&K] 【跟踪训练1】设正四棱锥SP1P2P3P4的所有棱长均为2,建立适当的空间直角坐标系,求、的坐标. 题型二 向量的平行与垂直 例2:如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点. 求证:(1)AM∥平面BDE; (2)AM⊥平面BDF. 【跟踪训练2】在正三棱锥P-ABC中,三条侧棱两两互相垂直,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2. 求证:(1)平面GEF⊥平面PBC;(2)EG⊥BC,PG⊥EG. 题型三 夹角与距离的计算 例3:如图,在直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点.(1)求BN的长; (2)求A1B与B1C所成角的余弦值; (3)求证:BN⊥平面C1MN.[来源:学+科+网] 【跟踪训练3】已知正三棱柱ABC-A1B1C1,底面边长AB=2,AB1⊥BC1,点O,O1分别是边AC,A1C1的中点.建立如图所示的空间直角坐标系. (1)求三棱柱的侧棱长. (2)M为BC1的中点,试用基向量,,表示向量. (3)求异面直线AB1与BC所成角的余弦值. 【课堂训练】1.已知向量a=(0,2,1),b=(-1,1,-2),则a与b的夹角为( ) A.0° B.45° C.90° D.180° 2.设A(3,3,1)、B(1,0,5)、C(0,1,0),则AB的中点M到C的距离CM的值为( ) A. B. C. D. 3.设O为坐标原点,M(5,-1,2),A(4,2,-1),若=,则点B应为( ) A.(-1,3,-3) B.(9,1,1) C.(1,-3,3) D.(-9,-1,-1) 4.若向量a=(1,1,x),b=(1,2,1),c=(1,1,1)满足条件(c-a)·(2b)=-2,则x的值为( ) A.2 B.-2 C.0 D.1 5.已知a=(1-t,1-t,t),b=(2,t,t),则|a-b|的最小值为( ) A. B. C. D.一、选择题 1.在空间直角坐标系Oxyz中,已知点A的坐标为(-1,2,1),点B的坐标为(1,3,4),则( ) A.=(-1,2,1) B.=(1,3,4) C.=(2,1,3) D.=(-2,-1,-3) 2.已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( ) A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)[来源:学科网]3.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( ) A.等腰三角形 B.等边三角形[来源:学科网]C.直角三角形 D.等腰直角三角形 4.已知向量a=(4,-2,-4),b=(6,-3,2),则下列结论正确的是( ) A.a+b=(10,-5,-6) B.a-b=(2,-1,-6) C.a·b=10 D.|a|=6 5.设O是正方形的中心,则向量,,是( ) A.有相同起点的向量 B.有相同终点的向量 C.相等的向量 D.模相等的向量 6.△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1),则AC边上的高BD等于( ) A.5 B. C.4 D.2 7.在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,则sin〈,〉的值为( ) A. B. C. D. 二、填空题 8.已知点A(1,2,1),B(-1,3,4),D(1,1,1),若=2,则||=________. 9.若a=(x,2,-4),b=(-1,y,3),c=(1,-2,z),且a,b,c两两垂直,则x=________,y=________,z=________. 10.与a=(2,-1,2)共线且满足a·z=-18的向量z的坐标为________. 11.已知2a+b=(0,-5,10),c=(1,-2,-2),a·c=4,|b|=12,则〈b,c〉=________. 三、解答题 12.已知A(1,0,0),B(0,-1,1),O(0,0,0),+λ与的夹角为120°,求λ的值. 13.如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=,CE=EF=1. (1)求证:AF∥平面BDE; (2)求证:CF⊥平面BDE. [来源:学_科_网]
知识点睛
题型分析
达标检测
