高数选修2-1同步1对1复习课程13 空间向量与空间角(无答案)
文档属性
| 名称 | 高数选修2-1同步1对1复习课程13 空间向量与空间角(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-18 11:35:58 | ||
图片预览



文档简介
全方位教学辅导教案
学 科 数 学 任课老师 [来源:学*科*网] 授课时间 ****年**月** 日 星期**
姓 名 性别 年级 高二 课次:第**次课
教 学 内 容 13空间向量与空间角
考 点 难 点 空间向量线线角,线面角空间向量与面面角,二面角的求法
知识点剖析和例题精讲
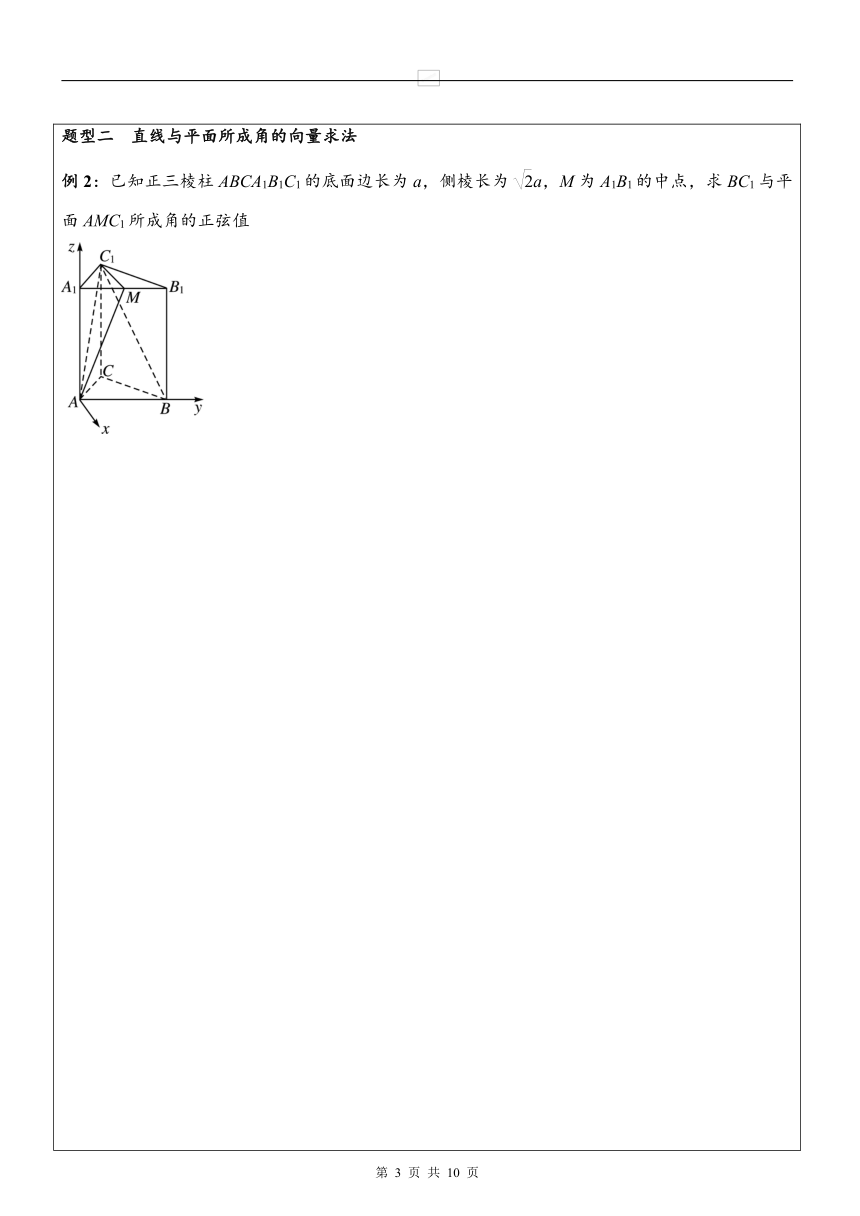
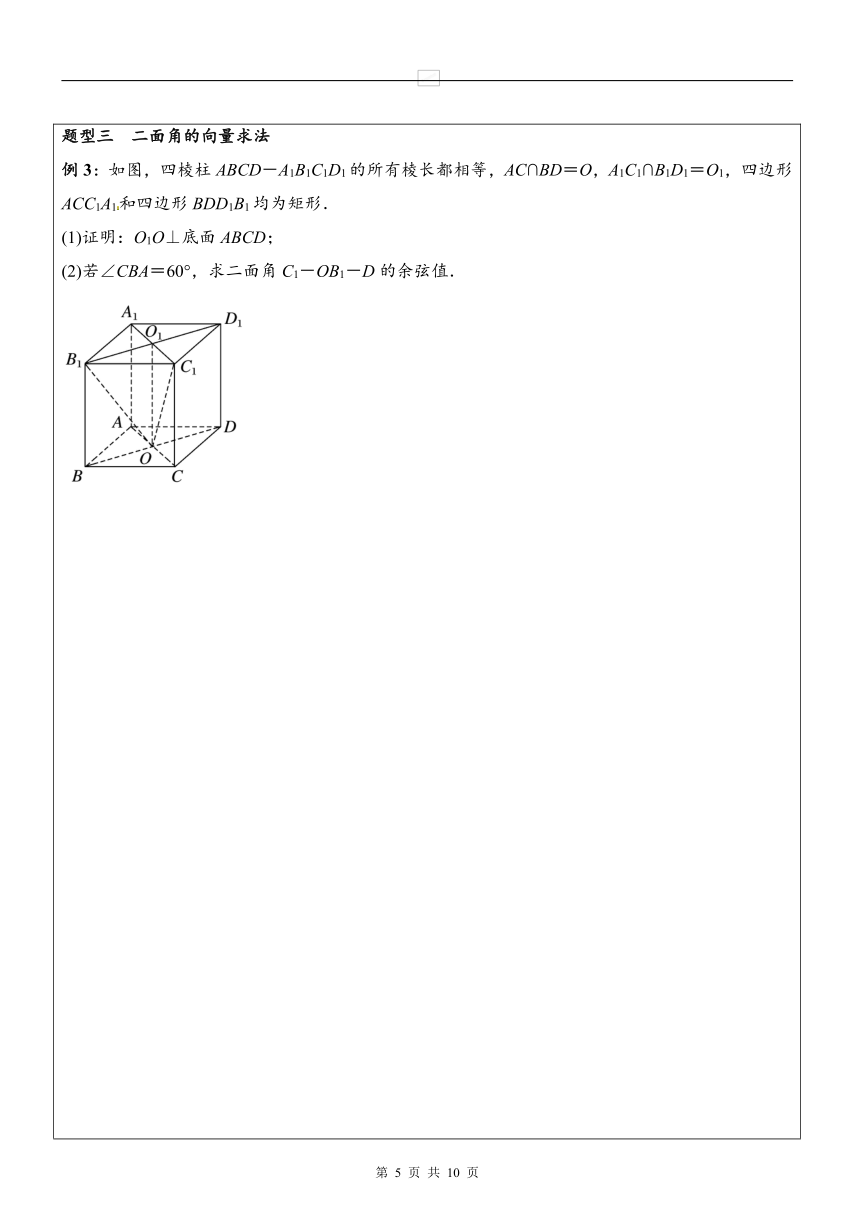
空间向量与空间角知识点一 两条异面直线所成的角①传统方法:解三角形②向量方法:; 知识点二 直线和平面所成的角①传统方法:解三角形②向量方法:;知识点三 二面角的平面角①传统方法:解三角形②向量方法:; 题型一 两条异面直线所成角的向量求法 例1:如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.求异面直线A1B与C1D所成角的余弦值. 【跟踪训练1】如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上的动点.若异面直线AD1与EC所成角为60°,试确定此时动点E的位置. 题型二 直线与平面所成角的向量求法 例2:已知正三棱柱ABCA1B1C1的底面边长为a,侧棱长为a,M为A1B1的中点,求BC1与平面AMC1所成角的正弦值 【跟踪训练2】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H. (1)求证:AB∥FG; (2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长. [来源:Z&xx&k.Com] [来源:学|科|网]题型三 二面角的向量求法 例3:如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形. (1)证明:O1O⊥底面ABCD; (2)若∠CBA=60°,求二面角C1-OB1-D的余弦值. 【跟踪训练3】如图所示,正三棱柱ABC—A1B1C1的所有棱长都为2,D为CC1的中点,求二面角AA1DB的余弦值. 【课堂训练】1.已知向量m,n分别是直线l和平面α的方向向量和法向量,若cos〈m,n〉=-,则直线l与平面α所成的角为( ) A.30° B.60° C.120° D.150° 2.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角的大小为( ) A.45° B.135° C.45°或135° D.90° 3.在正三棱柱ABCA1B1C1中,若AB=BB1,则AB1与C1B所成角的大小为( ) A.60° B.90° C.105° D.75° 4.正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的余弦值为( ) A. B. C. D. 5.在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,则异面直线A1B与B1C所成角的余弦值为________.一、选择题 1.若直线l的方向向量与平面α的法向量的夹角等于150°,则直线l与平面α所成的角等于( ) A.30° B.60° C.150° D.以上均错 2.直线l1,l2的方向向量分别是v1,v2,若v1与v2所成的角为θ,直线l1,l2所成的角为α,则( ) A.α=θ B.α=π-θ C.cos θ=|cos α| D.cos α=|cos θ| 3.在长方体ABCDA1B1C1D1中,AB=2,BC=2,DD1=3,则AC与BD1所成角的余弦值是( ) A.0 B. C.- D. 4.在正方体ABCD-A1B1C1D1中,M是AB的中点,则sin〈,〉的值等于( ) A. B. C. D. 5.已知正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于( ) A. B. C. D. 6.已知正四棱锥S-ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE、SD所成角的余弦值为( )A. B. C. D. 二、填空题 7.二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为________. 8.已知点A(1,0,0),B(0,2,0),C(0,0,3),则平面ABC与平面xOy所成锐二面角的余弦值为________. 9.已知正△ABC与正△BCD所在平面垂直,则二面角A-BD-C的正弦值为________. 10.已知直角△ABC的两条直角边BC=3,AC=4,PC⊥平面ABC,PC=,则点P到斜边AB的距离是________. 三、解答题[来源:学科网ZXXK]11.如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=AD. (1)求异面直线BF与DE所成的角的大小; (2)证明平面AMD⊥平面CDE; (3)求二面角ACDE的余弦值. 12.如图所示,在四面体ABCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=.求异面直线AB与CD所成角的余弦值. [来源:Z#xx#k.Com] 13.如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2. (1)证明:BD⊥AE; (2)求平面ADE和平面CDE所成角(锐角)的余弦值.
题型分析
达标检测
