高数选修2-1同步1对1复习课程14空间向量与立体几何本章复习(无答案)
文档属性
| 名称 | 高数选修2-1同步1对1复习课程14空间向量与立体几何本章复习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 567.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-18 11:35:20 | ||
图片预览




文档简介
全方位教学辅导教案
学 科 数 学 任课老师 授课时间 ****年**月** 日 星期**
姓 名 性别 年级 高二 课次:第**次课
教 学 内 容 14空间向量与立体几何本章复习
考 点 难 点 空间向量线线角,线面角空间向量与面面角,二面角的求法
知识点剖析和例题精讲
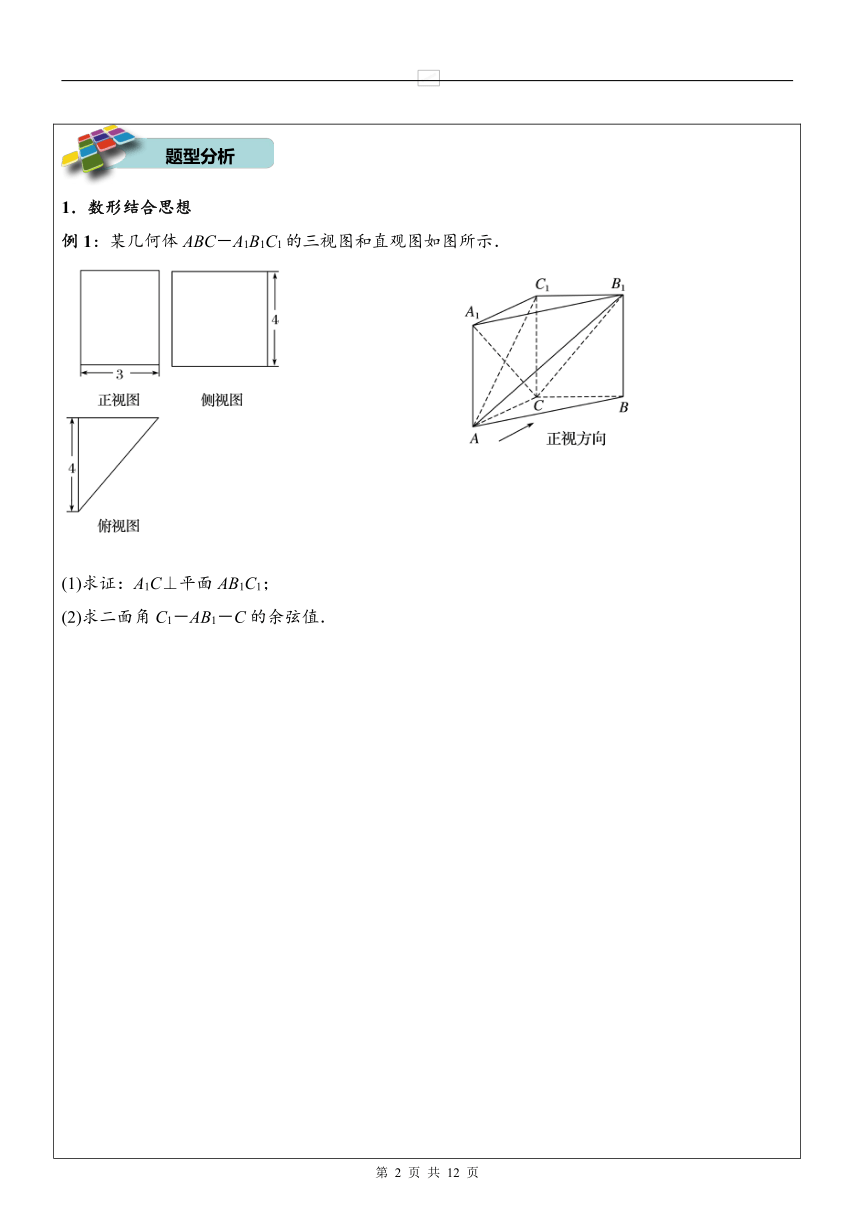
要点归纳1.空间向量的运算及运算律 空间向量加法、减法、数乘、向量的意义及运算律与平面向量类似,空间任意两个向量都可以通过平移转化为平面向量,两个向量相加的三角形法则与平行四边形法则仍然成立. 2.两个向量的数量积的计算 向量的数量积运算要遵循数量积的性质和运算律,常用于有关向量相等、两向量垂直、射影、夹角等问题中. 3.空间向量的坐标运算,关键是建立恰当的空间直角坐标系,然后再利用有关公式计算求解.常用向量的坐标运算来证明向量的垂直和平行问题,利用向量的夹角公式和距离公式求解空间角与空间距离的问题. 4.空间向量的基本定理说明:用三个不共面的已知向量{a,b,c}可以线性表示出空间任意一个向量,而且表示的结果是惟一的. 5.利用向量解决几何问题具有快捷、有效的特征.一般方法如下:先将原问题转化为等价的向量问题,即将已知条件中的角转化为向量的夹角,线段长度转化为向量的模,并用已知向量表示出未知向量,然后利用向量的运算解决该向量问题,从而原问题得解. 6.利用向量坐标解决立体几何问题的关键在于找准位置,建立适当、正确的空间直角坐标系,难点是在已建好的坐标系中表示出已知点的坐标,只有正确表示出已知点的坐标,才能通过向量的坐标运算,实现几何问题的代数化解法. 1.数形结合思想 例1:某几何体ABC-A1B1C1的三视图和直观图如图所示. (1)求证:A1C⊥平面AB1C1; (2)求二面角C1-AB1-C的余弦值. 【跟踪训练1】已知正方体ABCDA1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证: (1)FC1∥平面ADE; (2)平面ADE∥平面B1C1F. 2.转化和化归思想 例2:如图所示,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=EA=1. (1)求多面体EABCDF的体积; (2)求直线EB与平面ECF所成角的正弦值; (3)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明. 【跟踪训练2】如图,四棱锥FABCD的底面ABCD是菱形,其对角线AC=2,BD=.CF与平面ABCD垂直,CF=2.求二面角BAFD的大小. [来源:学,科,网] 3.方程思想 例3:如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点. (1)求直线AC与PB所成角的余弦值; (2)在侧面PAB内找一点N,使NE⊥平面PAC,并求出点N到AB的距离和点N到AP的距离. 【跟踪训练3】如图,在直三棱柱ABCA1B1C1中,AB=4,AC=BC=3,D为AB的中点. (1)求点C到平面A1ABB1的距离; (2)若AB1⊥A1C,求二面角A1CDC1的平面角的余弦值.[来源:学科网ZXXK] 1.如图,在三棱锥A-BCD中,AB=AC=AD=2,∠BAD=90°,∠BAC=60°,则·等于( ) A.-2 B.2 C.-2 D.2 2.在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=,则平面SCD与平面SAB所成二面角的余弦值为( ) A. B. C. D. 3.如图,AB=AC=BD=1,AB?平面M,AC⊥平面M,BD⊥AB,BD与平面M成30°角,则C、D间的距离为( ) A.1 B.2 D. [来源:学科网]4.如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是________. 5.如图,在四棱柱ABCDA1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和D1D的中点. (1)求证:MN∥平面ABCD;[来源:学科网ZXXK](2)求二面角D1ACB1的正弦值; (3)设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为,求线段A1E的长. 6.如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点. (1)证明:平面PAD⊥平面PCD; (2)求AC与PB的夹角的余弦值; (3)求二面角A-MC-B的余弦值. 6.如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.证明:PQ∥平面BCD. 7.如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点. (1)求证:AC⊥SD; (2)若SD⊥平面PAC,求二面角P-AC-D的大小; (3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值?若不存在,试说明理由. [来源:学+科+网Z+X+X+K]
题型分析
达标检测
