人教版必修四第一单元阅读与思考三角学与天文学课件(20张)
文档属性
| 名称 | 人教版必修四第一单元阅读与思考三角学与天文学课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览

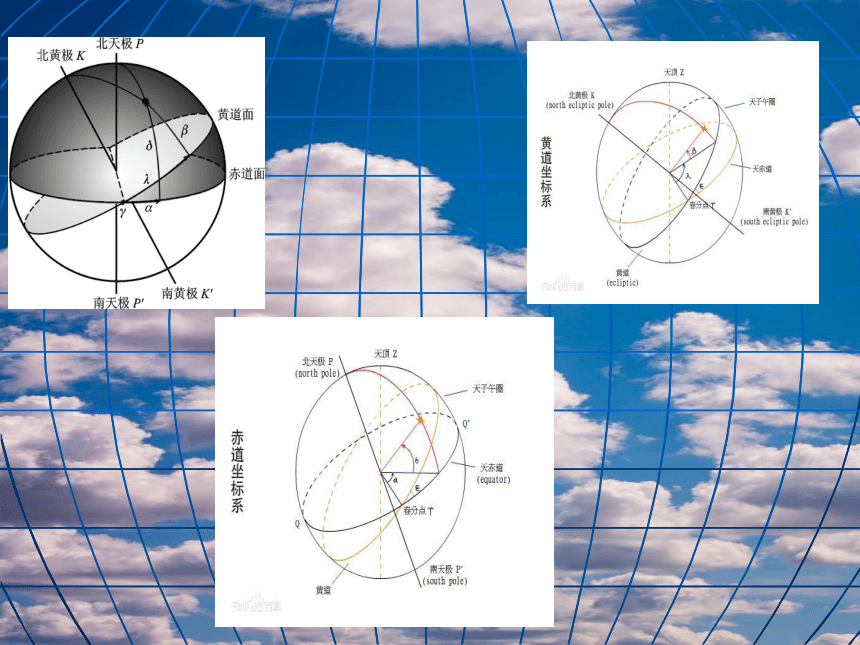







文档简介
课件20张PPT。高中数学必修四 人教A版
阅读与思考
三角学与天文学一、什么是三角学 三角学是以研究三角形的边和角的关系为基础,应用于测量为目的,同时也研究三角函数的性质及其应用的一门学科。三角学分为平面三角学与球面三角学。它们都是研究三角形中边与角之间的关系的学科。八大
星球二、三角学的分支及应用 三角学分为平面三角学与球面三角学。它们都是研究三角形中边与角之间的关系的学科。平面三角学分为角的度量、三角函数与反三角函数、诱导公式、和与差的公式、倍角、半角公式、和差化积与积化和差公式、解三角形等内容;球面三角学研究球面上由大圆弧构成的球面三角形的边与角之间的关系,在天文学、测量学、制图学、结晶学、仪器学等方面有广泛的应用。
雷格蒙塔努斯(Regiomontanus Johannes,1436—1476)德国数学家、天文学家。 弗朗索瓦·韦达(Fran?ois Viète,1540-1603)现代数学之父 约翰尼斯·开普勒(Johanns Kpler,1571—1630),杰出的德国天文学家第谷·布拉赫(Tycho Brah1546-1601),丹麦天文学家和占星学家 莱昂哈德·欧拉(Leonhard Euler ,1707年4月15日~1783年9月18日),瑞士数学家、自然科学家 三、不同时期著名人物简介在希腊 古希腊的自然科学家泰勒斯(公元前7世纪)的理论,可以认为是三角学的萌芽,但历史上都认为古希腊的天文学家喜帕恰斯是三角学的创始者。他著有三角学12卷,并作成弦表。可大都是天文观测的副产品.例如,古希腊门纳劳斯在公元100年左右著《球面学》,提出了三角学的基础问题和基本概念,特别是提出了球面三角学的门纳劳斯定理;50年后,另一个古希腊学者托勒密著《天文学大成》,初步发展了三角学。
喜帕恰斯 三角测量在中国也很早出现,公元前一百多年的《周髀算经》就有较详细的说明,例如它的首章记录“周公曰,大哉言数,请问用矩之道。商高曰,平矩以正绳,偃矩以望高,复矩以测深,卧矩以知远。”(商高说的矩就是今天工人用的两边互相垂直的曲尺,商高说的大意是将曲尺置于不同的位置可以测目标物的高度、深度与广度)。1世纪时的《九章算术》中有
专门研究测量问题的篇章。在中国中国古代在天文学方面的成就 在公元499年,印度数学家阿耶波多也表述出古代印度的三角学思想;其后的瓦拉哈米希拉最早引入正弦概念,并给出最早的正弦表;公元10世纪的一些阿拉伯学者进一步探讨了三角学。当然,所有这些工作都是天文学研究的组成部分。在印度阿耶波多 直到13世纪伊朗数学家纳西尔丁的《横截线原理书》才开始使三角学脱离天文学,成为纯粹数学的一个独立分支;而在欧洲,最早将三角学从天文学独立出来的数学家是15世纪的德国人雷格蒙塔努斯。他的主要著作是1464年完成的《论各种三角形》。著作。全书共5卷,前2卷论述平面三角学,后3卷讨论球面三角学,是欧洲传播三角学的源泉。雷格蒙塔努斯还较早地制成了一些三角函数表。雷格蒙塔努斯在欧洲四、三角学名称的来历 三角学一词的英文是trigonometry,来自拉丁文tuigonometuia。最先使用该词的是文艺复兴时期的德国数学家皮蒂斯楚斯,他在1595年出版的《三角学:解三角形的简明处理》中创造出这个词。它的构成法是由三角形(tuiangulum)和测量(metuicus)两字凑合而成。要测量计算离不开三角函数表和三角学公式,它们是作为三角学的主要内容而发展的。五、三角函数表 16世纪三角函数表的制作首推奥地利数学家雷蒂库斯(哥白尼的学生)。雷蒂库斯首次编制出全部6种三角函数的数表,包括第一张详尽的正切表和第一张印刷的正割表。
雷蒂库斯的主要贡献在三角学和天文学方面.1542年制作过半弦表,半径为1015,角度间隔以10'到1'不等,在表中雷蒂库斯首次给出余弦.他的《三角学准则》(1551)首次给出了六种三角函数表,包括正弦、余弦、正切、余切和正割、余割;重新定义了三角函数。即为直角三角形边与边的比,并指出比与角度有关,从而脱离了过去那种必须依赖圆弧的作法.他还给出大于45°角的函数与其余角(小于45°角)的函数相等.1562年,雷蒂库斯着手编制了更为精密的正弦、正切、正割表.计算这些表的数据,工作量相当大,雷蒂库斯工作12年之久,仍未在生前完成,后由他的学生奥托(Otto V.或Otho V.)完成出版.此外,他还深入研究过地理、天文、医学等。六、集大成者 文艺复兴后期,法国数学家韦达成为三角公式的集大成者。他的《应用于三角形的数学定律》(1579年)是较早系统论述平面和球面三角学的专著之一。给出精确到5位和10位小数的三角函数值,还附有与三角值有关的乘法表、商表等。第二部分给出造表的方法,解释了三角形中诸三角线量值关系的运算公式。除汇总前人的成果外,还补充了自己发现的新公式。如正切定律、和差化积公式等等。该书以直角三角形为基础。对斜三角形,韦达仿效古人的方法化为直角三角形来解决。对球面直角三角形,给出计算的完整公式及其记忆法则,如余弦定理,1591年韦达又得到多倍角关系式,1593 年又用三角方法推导出余弦定理。
。韦达七、对数的力量 17世纪初对数发明后大大简化了三角函数的计算,制作三角函数表已不再是很难的事,人们的注意力转向了三角学的理论研究。不过三角函数表的应用却一直占据重要地位,在科学研究与生产生活中发挥着不可替代的作用。对数发明者:纳皮尔八、棣莫弗定理和欧拉公式 1722年英国数学家棣莫弗得到以他的名字命名的三角学定理(cosθ±isinθ)^n=cosnθ+isinnθ,并证明了n是正有理数时公式成立;1748年欧拉证明了n是任意实数时公式也成立,他还给出另一个著名公式e^(iθ)=cosθ+isinθ,对三角学的发展起到了重要的推动作用。
近代三角学是从欧拉的《无穷分析引论》开始的.他定义了单位圆,并以函数线与半径的比值定义三角函数,他还创用小写拉丁字母a、b、c表示三角形三条边,大写拉丁字母A、B、C表示三角形三个角,从而简化了三角公式.使三角学从研究三角形 解法进一步转化为研究三角函数及其应用,成为一个比较完整的数学分支学科.而由于上述诸人及 19 世纪许多数学家的努力,形成了现代的三角函数符号和三角学的完整的理论。棣莫弗定理和欧拉公式棣莫弗欧拉具体应用厉害了,我的国
阅读与思考
三角学与天文学一、什么是三角学 三角学是以研究三角形的边和角的关系为基础,应用于测量为目的,同时也研究三角函数的性质及其应用的一门学科。三角学分为平面三角学与球面三角学。它们都是研究三角形中边与角之间的关系的学科。八大
星球二、三角学的分支及应用 三角学分为平面三角学与球面三角学。它们都是研究三角形中边与角之间的关系的学科。平面三角学分为角的度量、三角函数与反三角函数、诱导公式、和与差的公式、倍角、半角公式、和差化积与积化和差公式、解三角形等内容;球面三角学研究球面上由大圆弧构成的球面三角形的边与角之间的关系,在天文学、测量学、制图学、结晶学、仪器学等方面有广泛的应用。
雷格蒙塔努斯(Regiomontanus Johannes,1436—1476)德国数学家、天文学家。 弗朗索瓦·韦达(Fran?ois Viète,1540-1603)现代数学之父 约翰尼斯·开普勒(Johanns Kpler,1571—1630),杰出的德国天文学家第谷·布拉赫(Tycho Brah1546-1601),丹麦天文学家和占星学家 莱昂哈德·欧拉(Leonhard Euler ,1707年4月15日~1783年9月18日),瑞士数学家、自然科学家 三、不同时期著名人物简介在希腊 古希腊的自然科学家泰勒斯(公元前7世纪)的理论,可以认为是三角学的萌芽,但历史上都认为古希腊的天文学家喜帕恰斯是三角学的创始者。他著有三角学12卷,并作成弦表。可大都是天文观测的副产品.例如,古希腊门纳劳斯在公元100年左右著《球面学》,提出了三角学的基础问题和基本概念,特别是提出了球面三角学的门纳劳斯定理;50年后,另一个古希腊学者托勒密著《天文学大成》,初步发展了三角学。
喜帕恰斯 三角测量在中国也很早出现,公元前一百多年的《周髀算经》就有较详细的说明,例如它的首章记录“周公曰,大哉言数,请问用矩之道。商高曰,平矩以正绳,偃矩以望高,复矩以测深,卧矩以知远。”(商高说的矩就是今天工人用的两边互相垂直的曲尺,商高说的大意是将曲尺置于不同的位置可以测目标物的高度、深度与广度)。1世纪时的《九章算术》中有
专门研究测量问题的篇章。在中国中国古代在天文学方面的成就 在公元499年,印度数学家阿耶波多也表述出古代印度的三角学思想;其后的瓦拉哈米希拉最早引入正弦概念,并给出最早的正弦表;公元10世纪的一些阿拉伯学者进一步探讨了三角学。当然,所有这些工作都是天文学研究的组成部分。在印度阿耶波多 直到13世纪伊朗数学家纳西尔丁的《横截线原理书》才开始使三角学脱离天文学,成为纯粹数学的一个独立分支;而在欧洲,最早将三角学从天文学独立出来的数学家是15世纪的德国人雷格蒙塔努斯。他的主要著作是1464年完成的《论各种三角形》。著作。全书共5卷,前2卷论述平面三角学,后3卷讨论球面三角学,是欧洲传播三角学的源泉。雷格蒙塔努斯还较早地制成了一些三角函数表。雷格蒙塔努斯在欧洲四、三角学名称的来历 三角学一词的英文是trigonometry,来自拉丁文tuigonometuia。最先使用该词的是文艺复兴时期的德国数学家皮蒂斯楚斯,他在1595年出版的《三角学:解三角形的简明处理》中创造出这个词。它的构成法是由三角形(tuiangulum)和测量(metuicus)两字凑合而成。要测量计算离不开三角函数表和三角学公式,它们是作为三角学的主要内容而发展的。五、三角函数表 16世纪三角函数表的制作首推奥地利数学家雷蒂库斯(哥白尼的学生)。雷蒂库斯首次编制出全部6种三角函数的数表,包括第一张详尽的正切表和第一张印刷的正割表。
雷蒂库斯的主要贡献在三角学和天文学方面.1542年制作过半弦表,半径为1015,角度间隔以10'到1'不等,在表中雷蒂库斯首次给出余弦.他的《三角学准则》(1551)首次给出了六种三角函数表,包括正弦、余弦、正切、余切和正割、余割;重新定义了三角函数。即为直角三角形边与边的比,并指出比与角度有关,从而脱离了过去那种必须依赖圆弧的作法.他还给出大于45°角的函数与其余角(小于45°角)的函数相等.1562年,雷蒂库斯着手编制了更为精密的正弦、正切、正割表.计算这些表的数据,工作量相当大,雷蒂库斯工作12年之久,仍未在生前完成,后由他的学生奥托(Otto V.或Otho V.)完成出版.此外,他还深入研究过地理、天文、医学等。六、集大成者 文艺复兴后期,法国数学家韦达成为三角公式的集大成者。他的《应用于三角形的数学定律》(1579年)是较早系统论述平面和球面三角学的专著之一。给出精确到5位和10位小数的三角函数值,还附有与三角值有关的乘法表、商表等。第二部分给出造表的方法,解释了三角形中诸三角线量值关系的运算公式。除汇总前人的成果外,还补充了自己发现的新公式。如正切定律、和差化积公式等等。该书以直角三角形为基础。对斜三角形,韦达仿效古人的方法化为直角三角形来解决。对球面直角三角形,给出计算的完整公式及其记忆法则,如余弦定理,1591年韦达又得到多倍角关系式,1593 年又用三角方法推导出余弦定理。
。韦达七、对数的力量 17世纪初对数发明后大大简化了三角函数的计算,制作三角函数表已不再是很难的事,人们的注意力转向了三角学的理论研究。不过三角函数表的应用却一直占据重要地位,在科学研究与生产生活中发挥着不可替代的作用。对数发明者:纳皮尔八、棣莫弗定理和欧拉公式 1722年英国数学家棣莫弗得到以他的名字命名的三角学定理(cosθ±isinθ)^n=cosnθ+isinnθ,并证明了n是正有理数时公式成立;1748年欧拉证明了n是任意实数时公式也成立,他还给出另一个著名公式e^(iθ)=cosθ+isinθ,对三角学的发展起到了重要的推动作用。
近代三角学是从欧拉的《无穷分析引论》开始的.他定义了单位圆,并以函数线与半径的比值定义三角函数,他还创用小写拉丁字母a、b、c表示三角形三条边,大写拉丁字母A、B、C表示三角形三个角,从而简化了三角公式.使三角学从研究三角形 解法进一步转化为研究三角函数及其应用,成为一个比较完整的数学分支学科.而由于上述诸人及 19 世纪许多数学家的努力,形成了现代的三角函数符号和三角学的完整的理论。棣莫弗定理和欧拉公式棣莫弗欧拉具体应用厉害了,我的国
