人教版必修四1.1.4正弦余弦函数的图像课件(23张)
文档属性
| 名称 | 人教版必修四1.1.4正弦余弦函数的图像课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 742.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览




文档简介
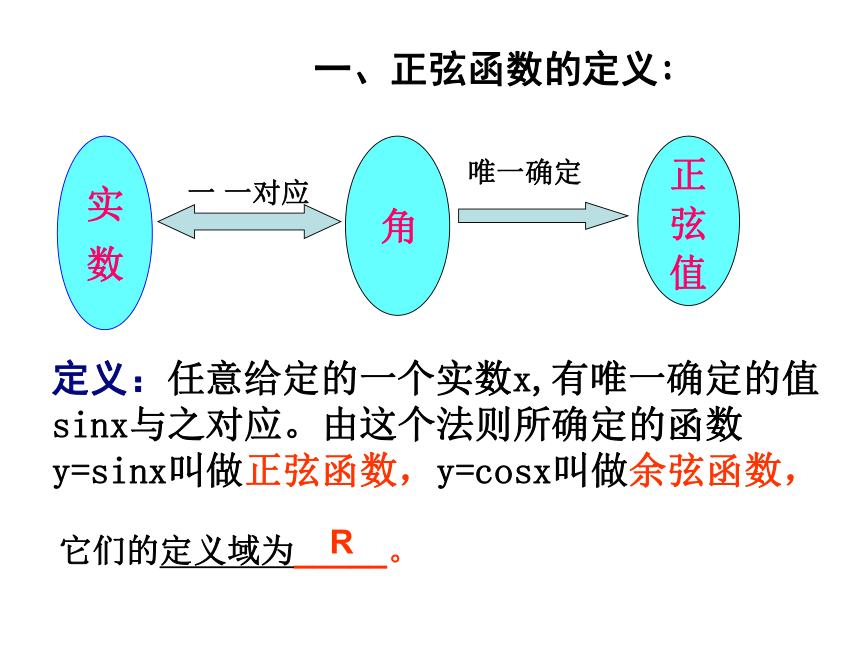
课件23张PPT。y=sinxy=cosx§1.4.1正弦余弦函数的图像定义:任意给定的一个实数x,有唯一确定的值sinx与之对应。由这个法则所确定的函数 y=sinx叫做正弦函数,y=cosx叫做余弦函数,实 数唯一确定一、正弦函数的定义:它们的定义域为_____。R遇到一个新的函数,先画出它的图象,然后通
过观察图象获得对它性质的直观认识, 是研
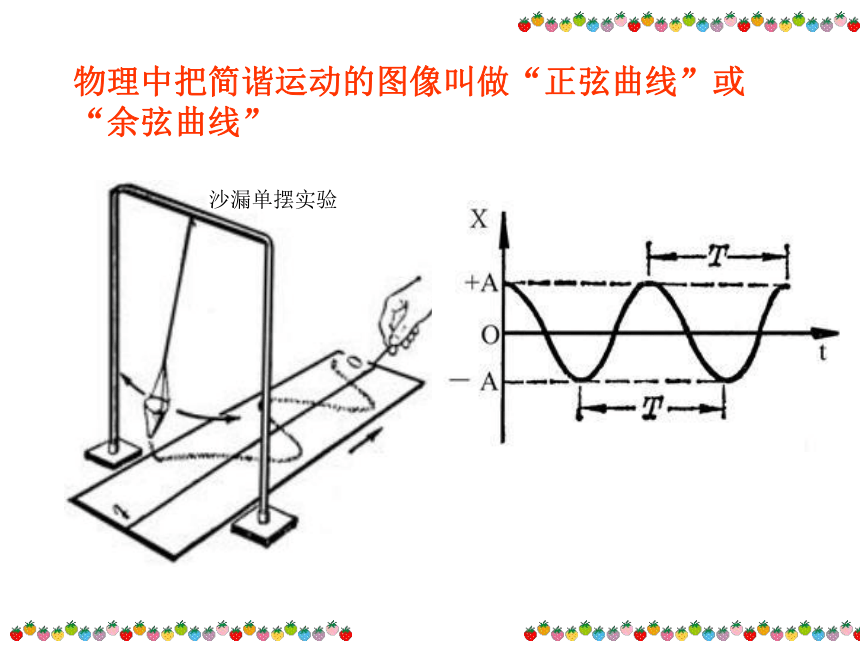
究函数的基本方法.正弦函数、余弦函数的图象物理中把简谐运动的图像叫做“正弦曲线”或“余弦曲线”沙漏单摆实验探究1:如何画出正弦函数 的图象?1、描点法作图的三个步骤:______、_______、_______。2、取哪些点?作图准确吗?3、为了得到比较精确的正弦函数图象,如何从几何的角
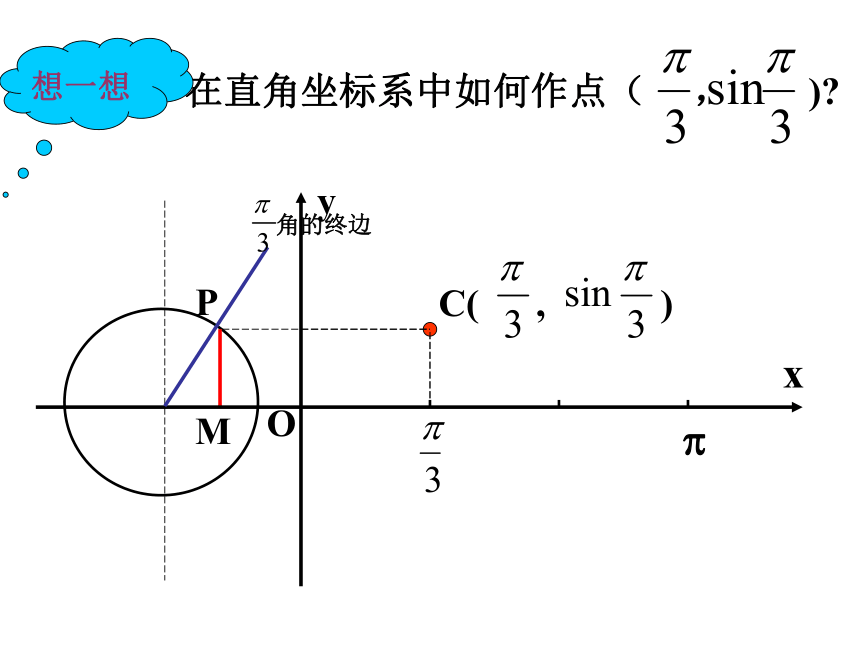
度用图形表示纵坐标?列表描点连线 在直角坐标系中如何作点( , )?
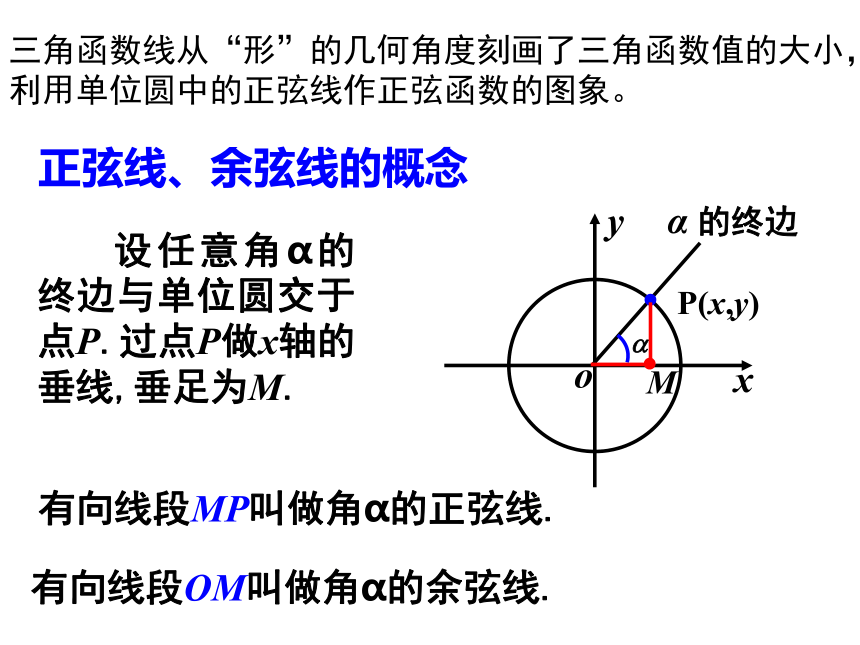
PM想一想正弦线、余弦线的概念 设任意角α的终边与单位圆交于点P.过点P做x轴的垂线,垂足为M.α 的终边P(x,y)M有向线段MP叫做角α的正弦线.有向线段OM叫做角α的余弦线.三角函数线从“形”的几何角度刻画了三角函数值的大小,
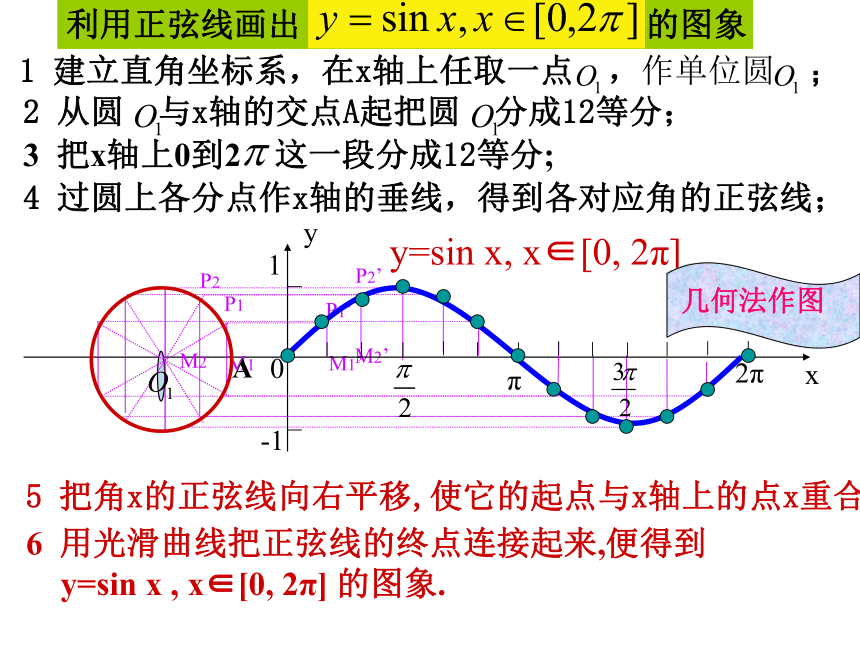
利用单位圆中的正弦线作正弦函数的图象。y=sin x, x∈[0, 2π]5 把角x的正弦线向右平移,使它的起点与x轴上的点x重合; 6 用光滑曲线把正弦线的终点连接起来,便得到
y=sin x , x∈[0, 2π] 的图象. 4 过圆上各分点作x轴的垂线,得到各对应角的正弦线; 利用正弦线画出 的图象y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z正弦函数y=sinx, x?R的图象叫正弦曲线.探究2:如何画出正弦函数 的图象?沿x轴左右平移余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同------平移变换我们在作正弦函数y=sinx ,x∈[0,2π]的图象时,描出了12个点,但其中起关键作用的点是哪些?分别说出它们的坐标。(0,0)( ? ,0)( 2? ,0)五个关键点—010-10最高点、最低点、与x轴的三个交点在精确度要求不高的情况下,我们常用“五点画图法”
作出正弦函数和余弦函数的简图。与x轴的交点图象的最高点图象的最低点图象中关键点正弦曲线与x轴的交点图象的最高点图象的最低点余弦曲线的五个关键点:10-101?五点作图法的步骤
①列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)“五点作图法”是我们画三角函数简图的基本方法。描点作图10-101-1010-1典型例题思考:能否从图象变换的角度出发得到(1)(2)的图象?列表(2)描点连线Y2X0 y=2sinx1y=sinx2.用图象变换法画出y=sin( -x),x∈[0, ]的简图;变式训练2.用图象变换法画出y=sin( -x),x∈[0, ]的简图;由诱导公式知1-1xyo思考:如何画出函数 的简图解法二:五点法作图解法一:图象变换:关于x轴作对称翻折2.注意与诱导公式、三角函数线等知识的联系y=sinx, x∈R的图象y=cosx, x∈R的图像.y=sinx, x∈R的图象 【课堂小结 】1. 正弦曲线、余弦曲线作法几何作图法(三角函数线)五点作图法图象变换法数形结合巧解题1若函数 的图象与直线
有且仅有两个不同的交点,求 的取值范围。
过观察图象获得对它性质的直观认识, 是研
究函数的基本方法.正弦函数、余弦函数的图象物理中把简谐运动的图像叫做“正弦曲线”或“余弦曲线”沙漏单摆实验探究1:如何画出正弦函数 的图象?1、描点法作图的三个步骤:______、_______、_______。2、取哪些点?作图准确吗?3、为了得到比较精确的正弦函数图象,如何从几何的角
度用图形表示纵坐标?列表描点连线 在直角坐标系中如何作点( , )?
PM想一想正弦线、余弦线的概念 设任意角α的终边与单位圆交于点P.过点P做x轴的垂线,垂足为M.α 的终边P(x,y)M有向线段MP叫做角α的正弦线.有向线段OM叫做角α的余弦线.三角函数线从“形”的几何角度刻画了三角函数值的大小,
利用单位圆中的正弦线作正弦函数的图象。y=sin x, x∈[0, 2π]5 把角x的正弦线向右平移,使它的起点与x轴上的点x重合; 6 用光滑曲线把正弦线的终点连接起来,便得到
y=sin x , x∈[0, 2π] 的图象. 4 过圆上各分点作x轴的垂线,得到各对应角的正弦线; 利用正弦线画出 的图象y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z正弦函数y=sinx, x?R的图象叫正弦曲线.探究2:如何画出正弦函数 的图象?沿x轴左右平移余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同------平移变换我们在作正弦函数y=sinx ,x∈[0,2π]的图象时,描出了12个点,但其中起关键作用的点是哪些?分别说出它们的坐标。(0,0)( ? ,0)( 2? ,0)五个关键点—010-10最高点、最低点、与x轴的三个交点在精确度要求不高的情况下,我们常用“五点画图法”
作出正弦函数和余弦函数的简图。与x轴的交点图象的最高点图象的最低点图象中关键点正弦曲线与x轴的交点图象的最高点图象的最低点余弦曲线的五个关键点:10-101?五点作图法的步骤
①列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)“五点作图法”是我们画三角函数简图的基本方法。描点作图10-101-1010-1典型例题思考:能否从图象变换的角度出发得到(1)(2)的图象?列表(2)描点连线Y2X0 y=2sinx1y=sinx2.用图象变换法画出y=sin( -x),x∈[0, ]的简图;变式训练2.用图象变换法画出y=sin( -x),x∈[0, ]的简图;由诱导公式知1-1xyo思考:如何画出函数 的简图解法二:五点法作图解法一:图象变换:关于x轴作对称翻折2.注意与诱导公式、三角函数线等知识的联系y=sinx, x∈R的图象y=cosx, x∈R的图像.y=sinx, x∈R的图象 【课堂小结 】1. 正弦曲线、余弦曲线作法几何作图法(三角函数线)五点作图法图象变换法数形结合巧解题1若函数 的图象与直线
有且仅有两个不同的交点,求 的取值范围。
