人教版必修五第一章解斜三角形应用举例课件(17张)
文档属性
| 名称 | 人教版必修五第一章解斜三角形应用举例课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 489.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览





文档简介
课件17张PPT。解斜三角形应用举例知 识 点 小 结1、正弦定理: 可以解决的有关解三角形问题:
(1)已知两角和任一边;
(2)已知两边和其中一边的对角。2、余弦定理:a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC可以解决的有关解三角形的问题:
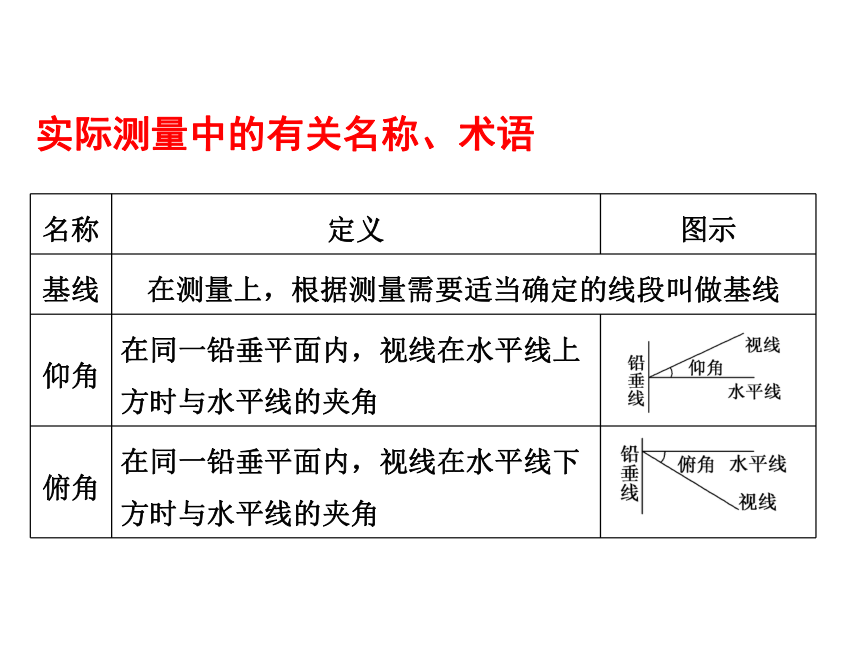
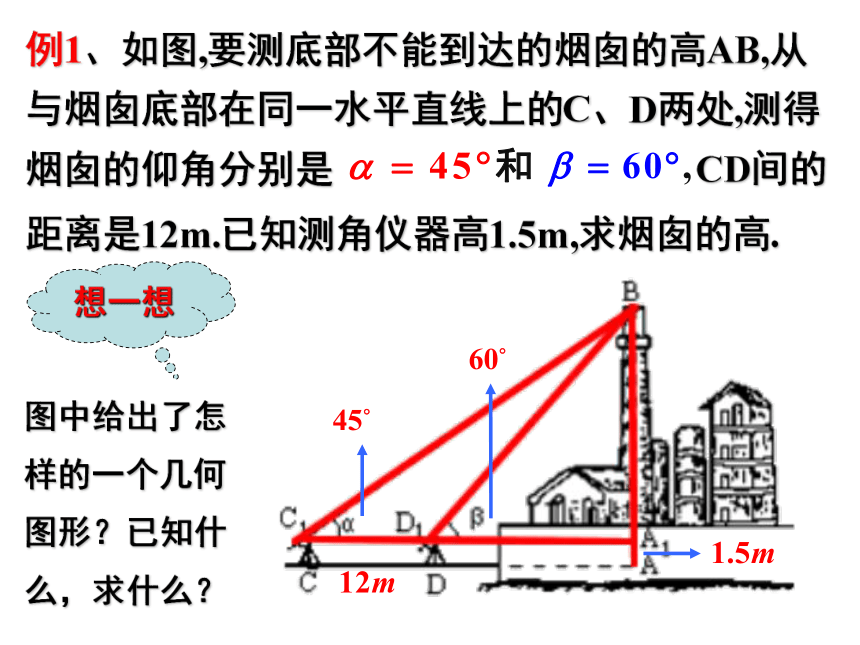
(1)已知三边;(2)已知两边和他们的夹角。实际测量中的有关名称、术语 例1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在同一水平直线上的C、D两处,测得烟囱的仰角分别是 CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高.图中给出了怎样的一个几何图形?已知什么,求什么?想一想分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:例2.我舰在敌岛A南偏西50?相距20海里的B处,发现敌舰正由岛A沿北偏西10?的方向以10海里/h的速度航行.问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰?解:故我舰行的方向为北偏东20?例3.如图,海中小岛A周围38海里内有暗礁,船正向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?解斜三角形应用题常见的几种情况:小结: 1.实际问题经抽象概括后,已知与未知量全部集中在一个三角形中,一次可用正弦定理或余弦定理解之. 2.实际问题经抽象概括后,已知量与未知量涉及两个三角形,这时需按顺序逐步在两个三角形中求出问题的解. 3.实际问题经抽象概括后,涉及的三角形只有一个, 但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.
(1)已知两角和任一边;
(2)已知两边和其中一边的对角。2、余弦定理:a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC可以解决的有关解三角形的问题:
(1)已知三边;(2)已知两边和他们的夹角。实际测量中的有关名称、术语 例1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在同一水平直线上的C、D两处,测得烟囱的仰角分别是 CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高.图中给出了怎样的一个几何图形?已知什么,求什么?想一想分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:例2.我舰在敌岛A南偏西50?相距20海里的B处,发现敌舰正由岛A沿北偏西10?的方向以10海里/h的速度航行.问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰?解:故我舰行的方向为北偏东20?例3.如图,海中小岛A周围38海里内有暗礁,船正向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?解斜三角形应用题常见的几种情况:小结: 1.实际问题经抽象概括后,已知与未知量全部集中在一个三角形中,一次可用正弦定理或余弦定理解之. 2.实际问题经抽象概括后,已知量与未知量涉及两个三角形,这时需按顺序逐步在两个三角形中求出问题的解. 3.实际问题经抽象概括后,涉及的三角形只有一个, 但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.
