人教版2.2.1向量的物理背景与概念及几何表示课件(24张)
文档属性
| 名称 | 人教版2.2.1向量的物理背景与概念及几何表示课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 154.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览





文档简介
课件24张PPT。2.1向量的物理背景与
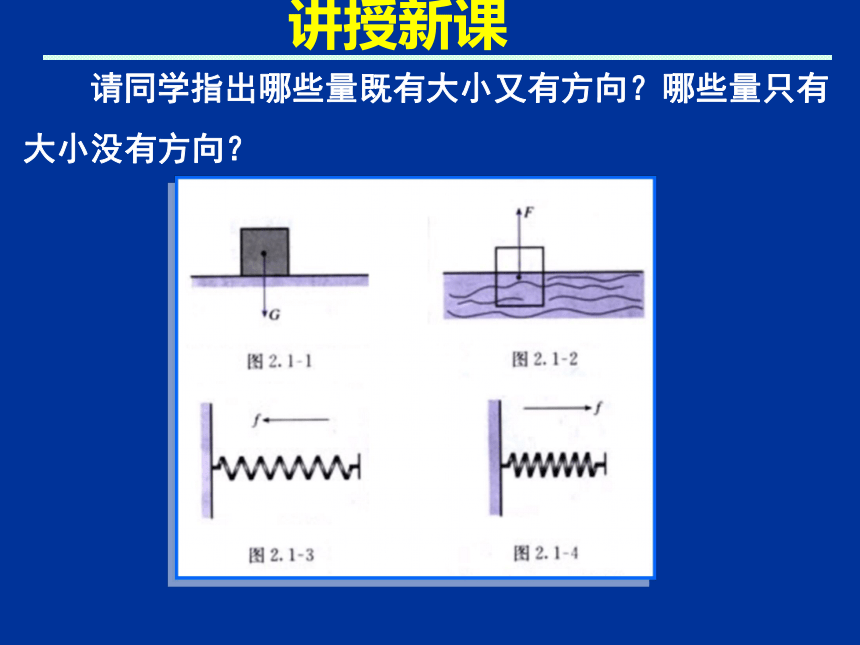
概念及几何表示 老鼠由A向西北逃窜,猫在B处向东追去,设问:猫能否追到老鼠? ABCD情境设置ABCD 猫的速度再快也没用,因为方向错了.结论:情境设置 老鼠由A向西北逃窜,猫在B处向东追去,设问:猫能否追到老鼠? 请同学指出哪些量既有大小又有方向?哪些量只有大小没有方向?讲授新课讲授新课1. 向量的概念:
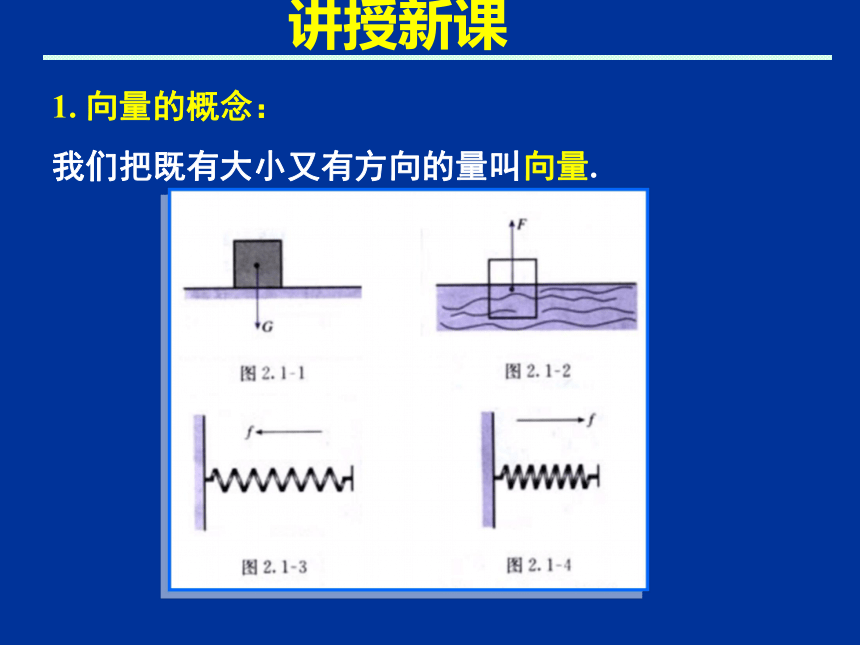
我们把既有大小又有方向的量叫向量.讲授新课1. 向量的概念:
我们把既有大小又有方向的量叫向量.讲授新课(1)数量与向量有何区别?
(2)如何表示向量?
(3)有向线段和线段有何区别和联系?分别可以表示向量的什么?
(4)长度为零的向量叫什么向量?长度为1的向量叫什么向量?阅读教材,回答下列问题:讲授新课(5)满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
(6)有一组向量,它们的方向相同或相反,这组向量有什么关系?
(7)如果把一组平行向量的起点全部移到一点O,这是它们是不是平行向量?这时各向量的终点之间有什么关系?阅读教材,回答下列问题:讲授新课A(起点) B
(终点)a 数量只有大小,是一个代数量,可以进行代数运算、比较大小;向量有方向,大小,双重性,不能比较大小. 2. 数量与向量的区别:讲授新课3. 向量的表示方法:①用有向线段表示;
②用字母a、b(黑体,印刷用)等表示;
③用有向线段的起点与终点字母:的大小——长度称为向量的模,向量记作.;讲授新课 具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.4. 有向线段:讲授新课 具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.
向量与有向线段的区别:4. 有向线段:讲授新课 具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.
向量与有向线段的区别:
(1)向量只有大小和方向两个要素,与起点无关,只要大小和方向相同,这两个向量就是相同的向量;
(2)有向线段有起点、大小和方向三个素,起点不同,尽管大小和方向相同,也是 不同的有向线段.4. 有向线段:讲授新课5. 零向量、单位向量概念:②长度为1个单位长度的向量, 叫单位向量.①长度为0的向量叫零向量,记作0.
0的方向是任意的.
注意0与0的含义与书写区别.讲授新课说明:
零向量、单位向量的定义都只是限制了大小.5. 零向量、单位向量概念:②长度为1个单位长度的向量, 叫单位向量.①长度为0的向量叫零向量,记作0.
0的方向是任意的.
注意0与0的含义与书写区别.讲授新课abc6.平行向量定义:①方向相同或相反的非零向量叫平行向量;
②我们规定0与任一向量平行.讲授新课abc说明:
(1) 综合①、②才是平行向量的完整定义;
(2) 向量a、b、c平行,记作a∥b∥c.6.平行向量定义:①方向相同或相反的非零向量叫平行向量;
②我们规定0与任一向量平行.讲授新课 例1. 如图,试根据图中的比例尺以及三地的位置,在图中分别用向量表示A地至B、C两地的位移,并求出A地至B、C两地的实际距离(精确到1km).ABC讲授新课例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?讲授新课例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?不一定讲授新课零向量例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?不一定讲授新课平行向量零向量例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?不一定讲授新课平行向量零向量不一定例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?描述向量的两个指标:模和方向.
2. 平面向量的概念和向量的几何表示;
3. 向量的模、零向量、单位向量、平行
向量等概念.课堂小结
概念及几何表示 老鼠由A向西北逃窜,猫在B处向东追去,设问:猫能否追到老鼠? ABCD情境设置ABCD 猫的速度再快也没用,因为方向错了.结论:情境设置 老鼠由A向西北逃窜,猫在B处向东追去,设问:猫能否追到老鼠? 请同学指出哪些量既有大小又有方向?哪些量只有大小没有方向?讲授新课讲授新课1. 向量的概念:
我们把既有大小又有方向的量叫向量.讲授新课1. 向量的概念:
我们把既有大小又有方向的量叫向量.讲授新课(1)数量与向量有何区别?
(2)如何表示向量?
(3)有向线段和线段有何区别和联系?分别可以表示向量的什么?
(4)长度为零的向量叫什么向量?长度为1的向量叫什么向量?阅读教材,回答下列问题:讲授新课(5)满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
(6)有一组向量,它们的方向相同或相反,这组向量有什么关系?
(7)如果把一组平行向量的起点全部移到一点O,这是它们是不是平行向量?这时各向量的终点之间有什么关系?阅读教材,回答下列问题:讲授新课A(起点) B
(终点)a 数量只有大小,是一个代数量,可以进行代数运算、比较大小;向量有方向,大小,双重性,不能比较大小. 2. 数量与向量的区别:讲授新课3. 向量的表示方法:①用有向线段表示;
②用字母a、b(黑体,印刷用)等表示;
③用有向线段的起点与终点字母:的大小——长度称为向量的模,向量记作.;讲授新课 具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.4. 有向线段:讲授新课 具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.
向量与有向线段的区别:4. 有向线段:讲授新课 具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.
向量与有向线段的区别:
(1)向量只有大小和方向两个要素,与起点无关,只要大小和方向相同,这两个向量就是相同的向量;
(2)有向线段有起点、大小和方向三个素,起点不同,尽管大小和方向相同,也是 不同的有向线段.4. 有向线段:讲授新课5. 零向量、单位向量概念:②长度为1个单位长度的向量, 叫单位向量.①长度为0的向量叫零向量,记作0.
0的方向是任意的.
注意0与0的含义与书写区别.讲授新课说明:
零向量、单位向量的定义都只是限制了大小.5. 零向量、单位向量概念:②长度为1个单位长度的向量, 叫单位向量.①长度为0的向量叫零向量,记作0.
0的方向是任意的.
注意0与0的含义与书写区别.讲授新课abc6.平行向量定义:①方向相同或相反的非零向量叫平行向量;
②我们规定0与任一向量平行.讲授新课abc说明:
(1) 综合①、②才是平行向量的完整定义;
(2) 向量a、b、c平行,记作a∥b∥c.6.平行向量定义:①方向相同或相反的非零向量叫平行向量;
②我们规定0与任一向量平行.讲授新课 例1. 如图,试根据图中的比例尺以及三地的位置,在图中分别用向量表示A地至B、C两地的位移,并求出A地至B、C两地的实际距离(精确到1km).ABC讲授新课例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?讲授新课例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?不一定讲授新课零向量例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?不一定讲授新课平行向量零向量例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?不一定讲授新课平行向量零向量不一定例2. 判断:
(1) 平行向量是否一定方向相同?
(2) 与任意向量都平行的向量是什么向量?
(3) 若两个向量在同一直线上,则这两个向量一定是什么向量?描述向量的两个指标:模和方向.
2. 平面向量的概念和向量的几何表示;
3. 向量的模、零向量、单位向量、平行
向量等概念.课堂小结
