人教版必修四2.2.5 向量在物理中的应用举例 课件(16张)
文档属性
| 名称 | 人教版必修四2.2.5 向量在物理中的应用举例 课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 256.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览






文档简介
课件16张PPT。2.5 平面向量应用举例 2.5.2 向量在物理中的应用举例 问题提出1.用向量方法解决平面几何问题的基本思路是什么?2.向量概念源于物理中的矢量,物理中的力、位移、速度等都是向量,功是向量的数量积,从而使得向量与物理学建立了有机的内在联系,物理中具有矢量意义的问题也可以转化为向量问题来解决.因此,在实际问题中,如何运用向量方法分析和解决物理问题,又是一个值得探讨的课题.向量在物理
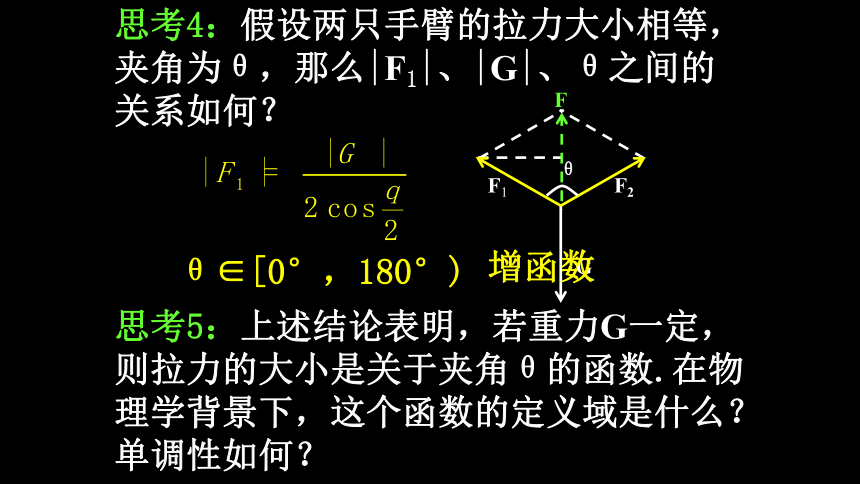
中的应用探究(一):向量在力学中的应用|F1|=|F2|=10NF1+F2+G=0思考2:两个人共提一个旅行包,或在单杠上做引体向上运动,根据生活经验,两只手臂的夹角大小与所耗力气的大小有什么关系?夹角越大越费力.思考3:若两只手臂的拉力为F1、F2,物体的重力为G,那么F1、F2、G三个力之间具有什么关系? F1+F2+G=0. 思考4:假设两只手臂的拉力大小相等,夹角为θ,那么|F1|、|G|、θ之间的关系如何?思考5:上述结论表明,若重力G一定,则拉力的大小是关于夹角θ的函数.在物理学背景下,这个函数的定义域是什么?单调性如何?θ∈[0°,180°)增函数 思考6:|F1|有最大值或最小值吗?|F1|与|G|可能相等吗?θ∈[0°,180°)当θ=0°时,|F1|有最小值,但没有最大值; 当θ=120°时,|F1|=|G|.探究(二):向量在运动学中的应用思考2:如果船沿与上游河岸成60°方向行驶,那么船的实际速度v的大小是多少? |v|2=| v1+v2|2=(v1+v2)2=84. 思考3:船应沿什么方向行驶,才能使航程最短?与上游河岸的夹角为78.73°.思考4:如果河的宽度d=500m,当航程最短时船行驶到对岸需要几分钟? 理论迁移 例1 一架飞机从A地向北偏西60°方向飞行1000km到达B地,然后向C地飞行,若C地在A地的南偏西60°方向,并且A、C两地相距2000km,求飞机从B地到C地的位移. 例2 一个物体受到同一平面内三个力F1、F2、F3的作用,沿北偏东45°方向移动了8m,已知|F1|=2N,方向为北偏东30°,|F2|=4N,方向为东偏北30°, |F3|=6N,方向为西偏北60°,求这三个力的合力所做的功.小结作业1.利用向量解决物理问题的基本步骤:①问题转化,即把物理问题转化为数学问题;②建立模型,即建立以向量为载体的数学模型;③求解参数,即求向量的模、夹角、数量积等;④回答问题,即把所得的数学结论回归到物理问题.2.用向量知识解决物理问题时,要注意数形结合.一般先要作出向量示意图,必要时可建立直角坐标系,再通过解三角形或坐标运算,求有关量的值. 3.向量源于物理中的矢量,运用向量方法可以解决物理中的矢量问题,这体现了认识来源于实践又服务于实践的辩证观点.作业
中的应用探究(一):向量在力学中的应用|F1|=|F2|=10NF1+F2+G=0思考2:两个人共提一个旅行包,或在单杠上做引体向上运动,根据生活经验,两只手臂的夹角大小与所耗力气的大小有什么关系?夹角越大越费力.思考3:若两只手臂的拉力为F1、F2,物体的重力为G,那么F1、F2、G三个力之间具有什么关系? F1+F2+G=0. 思考4:假设两只手臂的拉力大小相等,夹角为θ,那么|F1|、|G|、θ之间的关系如何?思考5:上述结论表明,若重力G一定,则拉力的大小是关于夹角θ的函数.在物理学背景下,这个函数的定义域是什么?单调性如何?θ∈[0°,180°)增函数 思考6:|F1|有最大值或最小值吗?|F1|与|G|可能相等吗?θ∈[0°,180°)当θ=0°时,|F1|有最小值,但没有最大值; 当θ=120°时,|F1|=|G|.探究(二):向量在运动学中的应用思考2:如果船沿与上游河岸成60°方向行驶,那么船的实际速度v的大小是多少? |v|2=| v1+v2|2=(v1+v2)2=84. 思考3:船应沿什么方向行驶,才能使航程最短?与上游河岸的夹角为78.73°.思考4:如果河的宽度d=500m,当航程最短时船行驶到对岸需要几分钟? 理论迁移 例1 一架飞机从A地向北偏西60°方向飞行1000km到达B地,然后向C地飞行,若C地在A地的南偏西60°方向,并且A、C两地相距2000km,求飞机从B地到C地的位移. 例2 一个物体受到同一平面内三个力F1、F2、F3的作用,沿北偏东45°方向移动了8m,已知|F1|=2N,方向为北偏东30°,|F2|=4N,方向为东偏北30°, |F3|=6N,方向为西偏北60°,求这三个力的合力所做的功.小结作业1.利用向量解决物理问题的基本步骤:①问题转化,即把物理问题转化为数学问题;②建立模型,即建立以向量为载体的数学模型;③求解参数,即求向量的模、夹角、数量积等;④回答问题,即把所得的数学结论回归到物理问题.2.用向量知识解决物理问题时,要注意数形结合.一般先要作出向量示意图,必要时可建立直角坐标系,再通过解三角形或坐标运算,求有关量的值. 3.向量源于物理中的矢量,运用向量方法可以解决物理中的矢量问题,这体现了认识来源于实践又服务于实践的辩证观点.作业
