人教版必修四第二单元平面向量复习课件(27张)
文档属性
| 名称 | 人教版必修四第二单元平面向量复习课件(27张) | 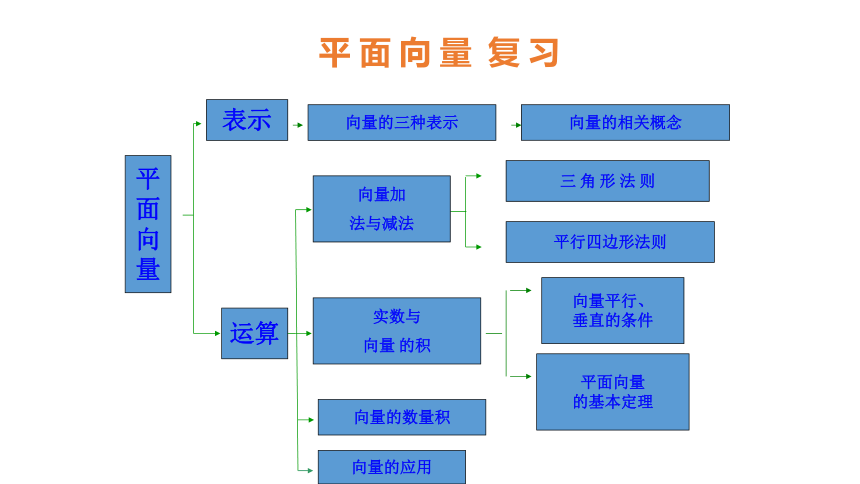 | |
| 格式 | zip | ||
| 文件大小 | 360.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 12:37:31 | ||
图片预览






文档简介
课件27张PPT。平 面 向 量 复 习向量的三种表示表示运算向量加
法与减法向量的相关概念实数与
向量 的积三 角 形 法 则平行四边形法则向量平行、
垂直的条件平面向量
的基本定理平
面
向
量向量的数量积向量的应用几何表示 : 有向线段向量的表示字母表示 坐标表示 : (x,y)若 A(x1,y1), B(x2,y2)则 AB = (x2 - x1 , y2 - y1)1.向量的概念:
2.向量的表示:
3.零向量:
4.单位向量:
5.平行向量:
6.相等向量:
7.共线向量:既有大小又有方向的量1.有向线段 2.字母
3.有向线段起点和终点字母长度为零的向量(零向量与任意向量都平行长度为1个单位的向量1.方向相同或相反的非零向量
2.零向量与任一向量平行长度相等且方向相同的向量平行向量就是共线向量向量的模(长度)1. 设 a = ( x , y ),则2. 若表示向量 a 的起点和终点的坐标分别
为A(x1,y1)、B (x2,y2) ,则例1:思考下列问题:1、下列命题正确的是
(1)共线向量都相等
(2)单位向量都相等
(3)平行向量不一定是共线向量
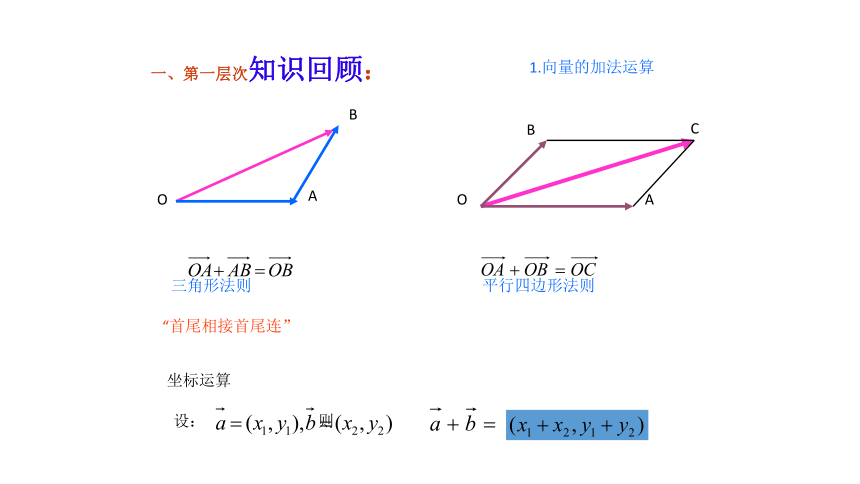
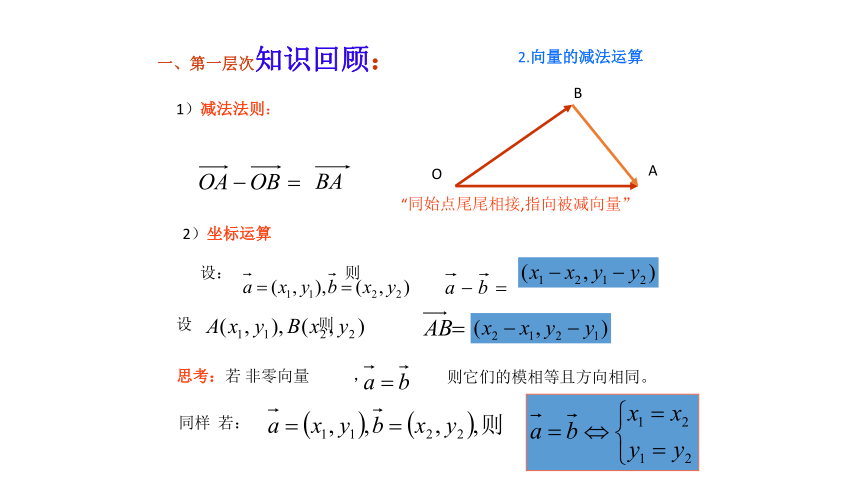
(4)零向量与任一向量平行四、例题一、第一层次知识回顾:1.向量的加法运算“首尾相接首尾连”2.向量的减法运算思考:若 非零向量 ,则它们的模相等且方向相同。
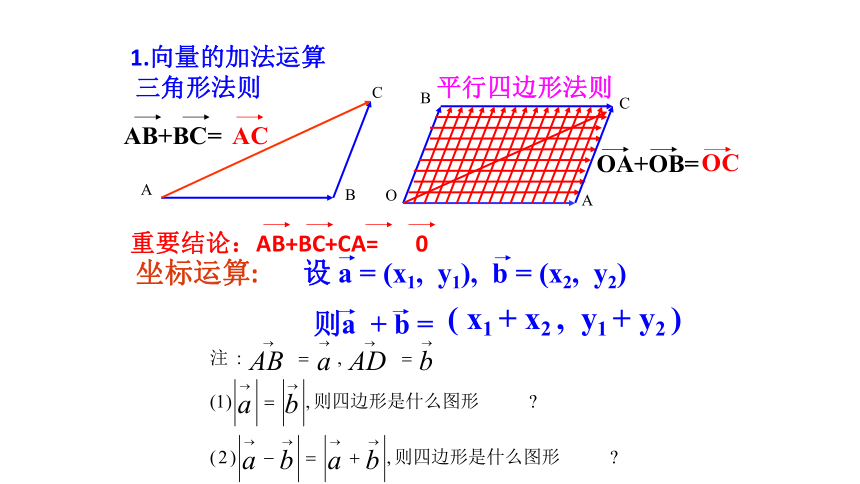
同样 若:“同始点尾尾相接,指向被减向量”一、第一层次知识回顾:1.向量的加法运算ABC AB+BC=三角形法则OABC OA+OB=平行四边形法则坐标运算:则a + b =重要结论:AB+BC+CA= 0设 a = (x1, y1), b = (x2, y2)( x1 + x2 , y1 + y2 )AC OC例题:实数λ与向量 a 的积定义:坐标运算:其实质就是向量的伸长或缩短!λa是一个向量.它的长度 |λa| =|λ| |a|;它的方向(1) 当λ≥0时,λa 的方向与a方向相同;(2) 当λ<0时,λa 的方向与a方向相反.若a = (x , y), 则λa = λ (x , y)= (λ x , λ y)平面向量的数量积
(1)a与b的夹角:
(2)向量夹角的范围:
(3)向量垂直:
[00 ,1800]共同的起点(4)两个非零向量的数量积: 规定:零向量与任一向量的数量积为0a · b = |a| |b| cosθ几何意义:数量积 a ·b 等于 a 的长度 |a|与 b 在 a 的方向上的投影 |b| cosθ的乘积。若 a=( x1, y1 ), b=( x2, y2 )则a · b= x1 · x2 + y1 · y25、数量积的运算律:⑴交换律:⑵对数乘的结合律:⑶分配律:注意:数量积不满足结合律5、重要定理和公式:
二、平面向量之间关系向量平行(共线)条件的两种形式:向量垂直条件的两种形式:3、平面向量的坐标运算—知识回忆知识回忆典例分析例5例6例题解这个方程组得k=-(1/3), λ=-(1/3),即当k=-(1/3)时,
ka+b与a-3b平行,这时
ka+b=-a/3+b.
因为λ=-(1/3)<0,所以-a/3+b与a-3b反向。 在本例中,也可以根据向量平行充分条件的坐标
形式,从(k-3)?(-4)-10?(2k+2)=0,先解出
k=-(1/3),然后再求λ。注例2 设a,b是两个不共线向量。
AB=2a+kb BC=a+b CD=a-2b
A、B、D共线则k=_____(k∈R)知识回忆典例分析例2例3例42、实数与向量的积—典例分析-例21.与平面几何的结合: CC四边形ABCD是菱形四边形ABCD是矩形ODMOM外心重心重心第一层次例题分析类型四:三角形中的向量问题重要结论:ABCO第一层次例题分析类型四:三角形中的向量问题练习1:判断正误,并简述理由。( √ )( √ )( √ )( × )( × )( × )平 面 向 量 复 习2.设AB=2(a+5b),BC= ?2a + 8b,CD=3(a ?b),
求证:A、B、D 三点共线。 分析要证A、B、D三点共线,可证AB=λBD关键是找到λ解:∵BD=BC+CD= ?2a + 8b+ 3(a ?b)=a+5b∴AB=2 BD且AB与BD有公共点B∴ A、B、D 三点共线AB∥ BD
法与减法向量的相关概念实数与
向量 的积三 角 形 法 则平行四边形法则向量平行、
垂直的条件平面向量
的基本定理平
面
向
量向量的数量积向量的应用几何表示 : 有向线段向量的表示字母表示 坐标表示 : (x,y)若 A(x1,y1), B(x2,y2)则 AB = (x2 - x1 , y2 - y1)1.向量的概念:
2.向量的表示:
3.零向量:
4.单位向量:
5.平行向量:
6.相等向量:
7.共线向量:既有大小又有方向的量1.有向线段 2.字母
3.有向线段起点和终点字母长度为零的向量(零向量与任意向量都平行长度为1个单位的向量1.方向相同或相反的非零向量
2.零向量与任一向量平行长度相等且方向相同的向量平行向量就是共线向量向量的模(长度)1. 设 a = ( x , y ),则2. 若表示向量 a 的起点和终点的坐标分别
为A(x1,y1)、B (x2,y2) ,则例1:思考下列问题:1、下列命题正确的是
(1)共线向量都相等
(2)单位向量都相等
(3)平行向量不一定是共线向量
(4)零向量与任一向量平行四、例题一、第一层次知识回顾:1.向量的加法运算“首尾相接首尾连”2.向量的减法运算思考:若 非零向量 ,则它们的模相等且方向相同。
同样 若:“同始点尾尾相接,指向被减向量”一、第一层次知识回顾:1.向量的加法运算ABC AB+BC=三角形法则OABC OA+OB=平行四边形法则坐标运算:则a + b =重要结论:AB+BC+CA= 0设 a = (x1, y1), b = (x2, y2)( x1 + x2 , y1 + y2 )AC OC例题:实数λ与向量 a 的积定义:坐标运算:其实质就是向量的伸长或缩短!λa是一个向量.它的长度 |λa| =|λ| |a|;它的方向(1) 当λ≥0时,λa 的方向与a方向相同;(2) 当λ<0时,λa 的方向与a方向相反.若a = (x , y), 则λa = λ (x , y)= (λ x , λ y)平面向量的数量积
(1)a与b的夹角:
(2)向量夹角的范围:
(3)向量垂直:
[00 ,1800]共同的起点(4)两个非零向量的数量积: 规定:零向量与任一向量的数量积为0a · b = |a| |b| cosθ几何意义:数量积 a ·b 等于 a 的长度 |a|与 b 在 a 的方向上的投影 |b| cosθ的乘积。若 a=( x1, y1 ), b=( x2, y2 )则a · b= x1 · x2 + y1 · y25、数量积的运算律:⑴交换律:⑵对数乘的结合律:⑶分配律:注意:数量积不满足结合律5、重要定理和公式:
二、平面向量之间关系向量平行(共线)条件的两种形式:向量垂直条件的两种形式:3、平面向量的坐标运算—知识回忆知识回忆典例分析例5例6例题解这个方程组得k=-(1/3), λ=-(1/3),即当k=-(1/3)时,
ka+b与a-3b平行,这时
ka+b=-a/3+b.
因为λ=-(1/3)<0,所以-a/3+b与a-3b反向。 在本例中,也可以根据向量平行充分条件的坐标
形式,从(k-3)?(-4)-10?(2k+2)=0,先解出
k=-(1/3),然后再求λ。注例2 设a,b是两个不共线向量。
AB=2a+kb BC=a+b CD=a-2b
A、B、D共线则k=_____(k∈R)知识回忆典例分析例2例3例42、实数与向量的积—典例分析-例21.与平面几何的结合: CC四边形ABCD是菱形四边形ABCD是矩形ODMOM外心重心重心第一层次例题分析类型四:三角形中的向量问题重要结论:ABCO第一层次例题分析类型四:三角形中的向量问题练习1:判断正误,并简述理由。( √ )( √ )( √ )( × )( × )( × )平 面 向 量 复 习2.设AB=2(a+5b),BC= ?2a + 8b,CD=3(a ?b),
求证:A、B、D 三点共线。 分析要证A、B、D三点共线,可证AB=λBD关键是找到λ解:∵BD=BC+CD= ?2a + 8b+ 3(a ?b)=a+5b∴AB=2 BD且AB与BD有公共点B∴ A、B、D 三点共线AB∥ BD
