人教版必修四1.1.4正弦函数的图像课件(17张)
文档属性
| 名称 | 人教版必修四1.1.4正弦函数的图像课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 429.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览


文档简介
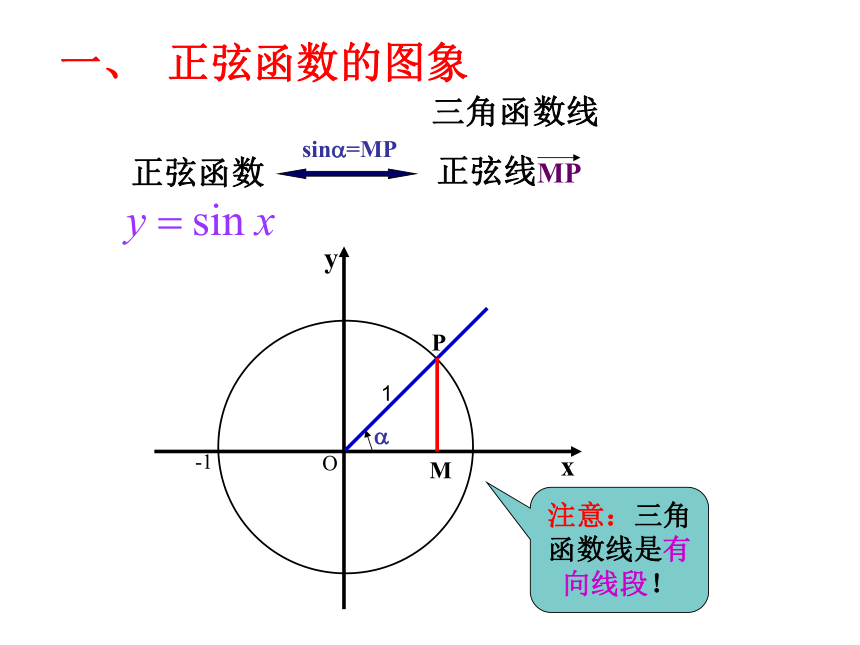
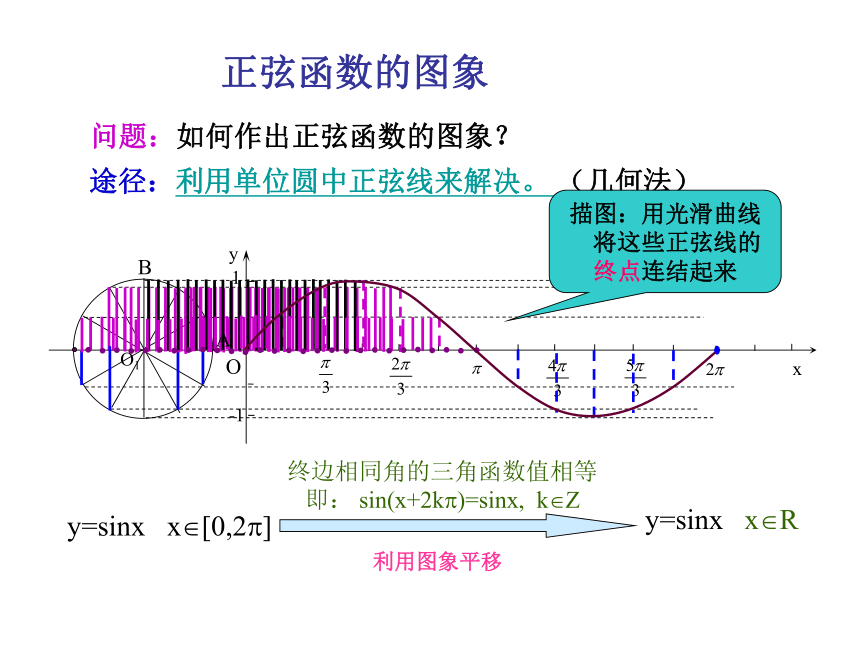
课件17张PPT。三角函数的图象与性质正弦函数的图象三角函数线正弦函数一、 正弦函数的图象 PMsin?=MP注意:三角函数线是有向线段!1 正弦函数的图象 问题:如何作出正弦函数的图象?途径:利用单位圆中正弦线来解决。 (几何法)y=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 描图:用光滑曲线
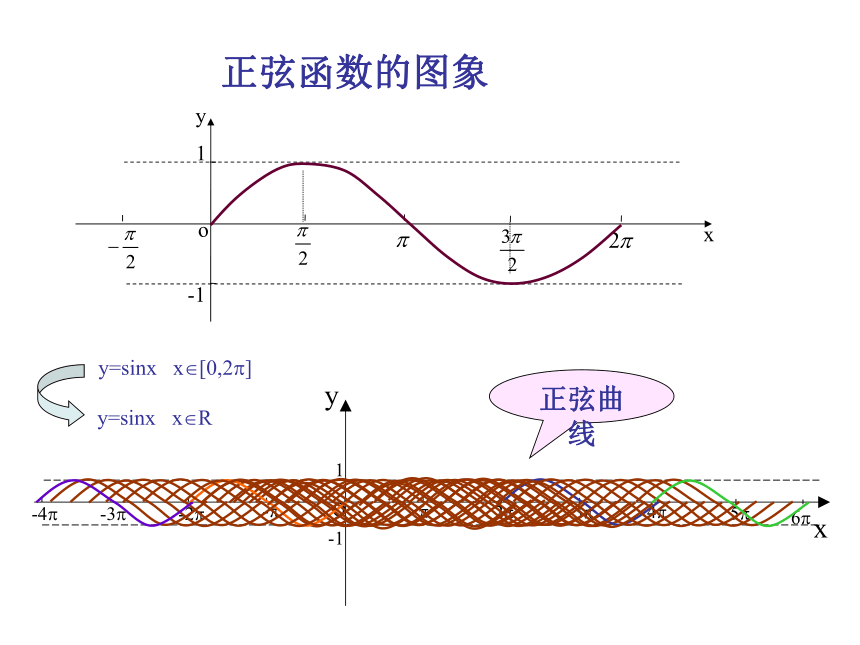
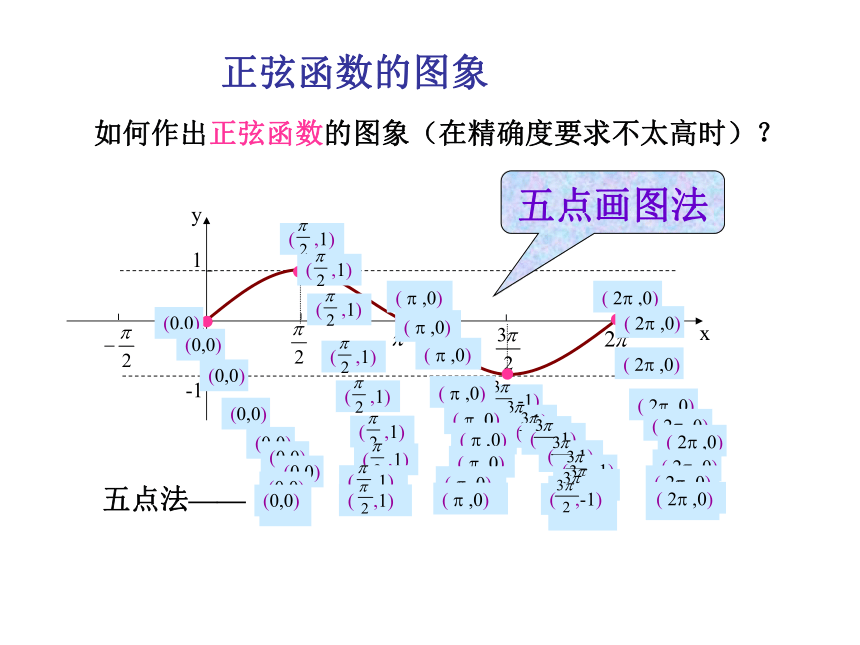
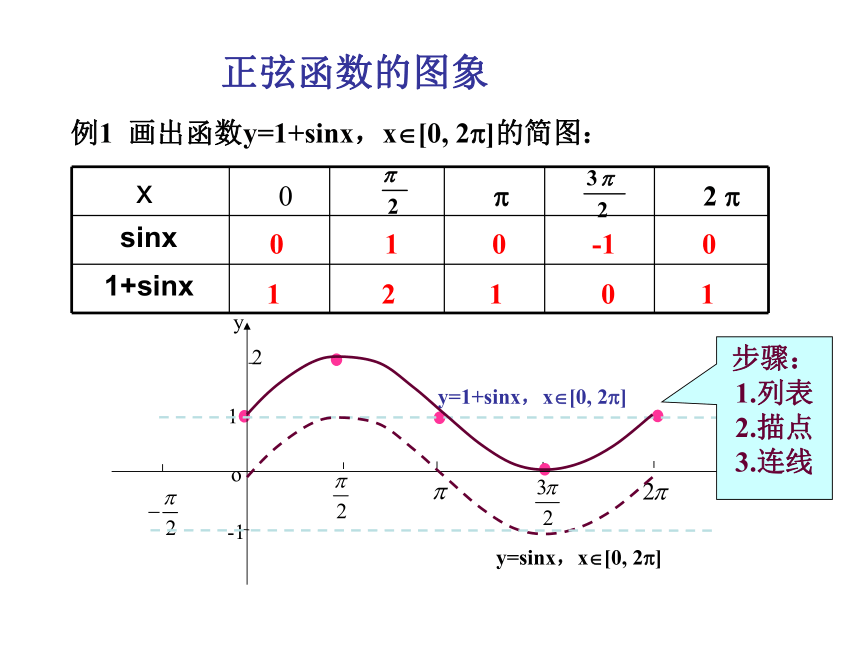
将这些正弦线的终点连结起来利用图象平移AB 正弦函数的图象 y=sinx x?[0,2?]y=sinx x?R正弦曲线 正弦函数的图象 如何作出正弦函数的图象(在精确度要求不太高时)?(0,0)( ? ,0)( 2? ,0)五点画图法五点法—— 正弦函数的图象 例1 画出函数y=1+sinx,x?[0, 2?]的简图:12101 0 1 0 -1 0 xo1y-12y=sinx,x?[0, 2?]y=1+sinx,x?[0, 2?]步骤:
1.列表
2.描点
3.连线 正弦函数的图象 小
结1. 正弦曲线2.注意与诱导公式、三角函数线等知识的联系y=sinx,x?[0, 2?] 二、 正弦函数的性质 y=sinx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2? 正弦函数的奇偶性sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数定义域关于原点对称 正弦函数的奇偶性、单调性 y=sinxy=sinx (x?R) 图象关于原点对称 正弦函数的单调性 y=sinx (x?R)-1 0 1 0 -1 正弦函数的单调性 y=cosx (x?R)-1 0 1 0 -1 正弦函数的奇偶性、单调性的例解:例2 求下列函数的单调区间: (1) y=2sin(-x )解: y=2sin(-x )= -2sinx 所以:解:解:则 y= -|sinu| 大致图象如下:减区间为增区间为即:小 结: 正弦、余弦函数的奇偶性、单调性 奇偶性 单调性(单调区间)奇函数偶函数单调递增单调递减函数求函数的单调区间:1. 直接利用相关性质2. 复合函数的单调性3. 利用图象寻找单调区间
将这些正弦线的终点连结起来利用图象平移AB 正弦函数的图象 y=sinx x?[0,2?]y=sinx x?R正弦曲线 正弦函数的图象 如何作出正弦函数的图象(在精确度要求不太高时)?(0,0)( ? ,0)( 2? ,0)五点画图法五点法—— 正弦函数的图象 例1 画出函数y=1+sinx,x?[0, 2?]的简图:12101 0 1 0 -1 0 xo1y-12y=sinx,x?[0, 2?]y=1+sinx,x?[0, 2?]步骤:
1.列表
2.描点
3.连线 正弦函数的图象 小
结1. 正弦曲线2.注意与诱导公式、三角函数线等知识的联系y=sinx,x?[0, 2?] 二、 正弦函数的性质 y=sinx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2? 正弦函数的奇偶性sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数定义域关于原点对称 正弦函数的奇偶性、单调性 y=sinxy=sinx (x?R) 图象关于原点对称 正弦函数的单调性 y=sinx (x?R)-1 0 1 0 -1 正弦函数的单调性 y=cosx (x?R)-1 0 1 0 -1 正弦函数的奇偶性、单调性的例解:例2 求下列函数的单调区间: (1) y=2sin(-x )解: y=2sin(-x )= -2sinx 所以:解:解:则 y= -|sinu| 大致图象如下:减区间为增区间为即:小 结: 正弦、余弦函数的奇偶性、单调性 奇偶性 单调性(单调区间)奇函数偶函数单调递增单调递减函数求函数的单调区间:1. 直接利用相关性质2. 复合函数的单调性3. 利用图象寻找单调区间
