人教版必修四3.3.1两角差的余弦公式课件(19张)
文档属性
| 名称 | 人教版必修四3.3.1两角差的余弦公式课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 351.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览



文档简介
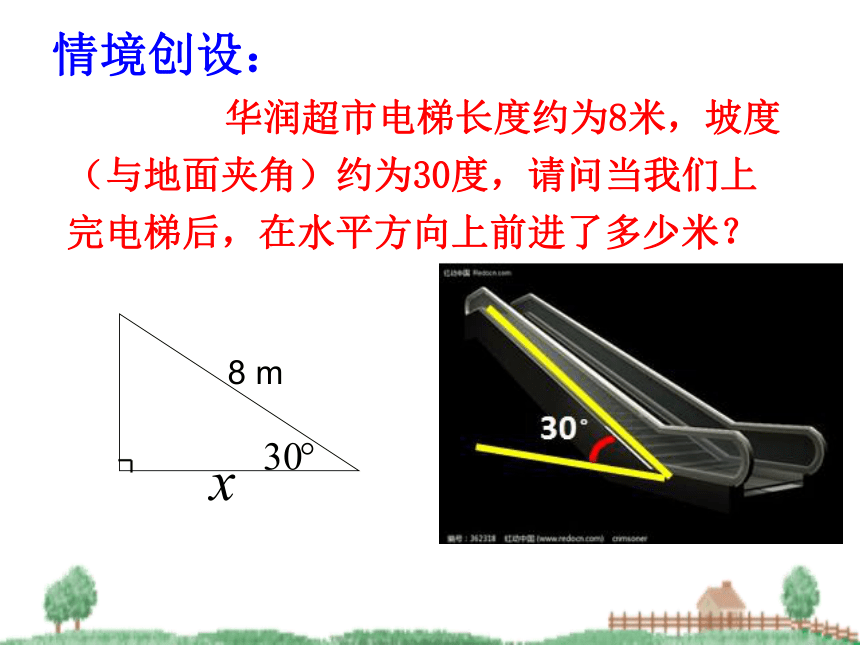
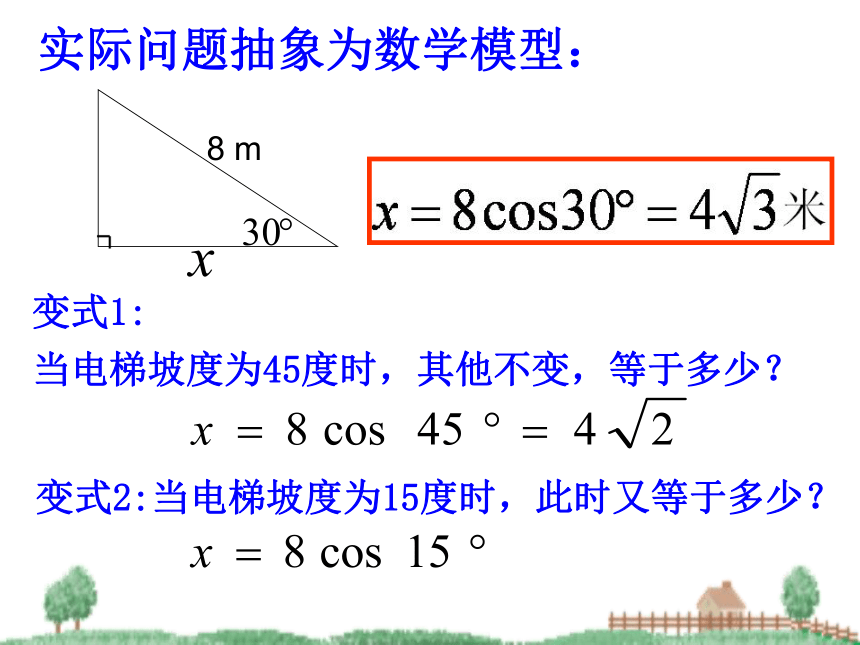
课件19张PPT。第三章 三角恒等变换3.1.1两角和与差的余弦公式 华润超市电梯长度约为8米,坡度(与地面夹角)约为30度,请问当我们上完电梯后,在水平方向上前进了多少米?情境创设:实际问题抽象为数学模型:变式1:
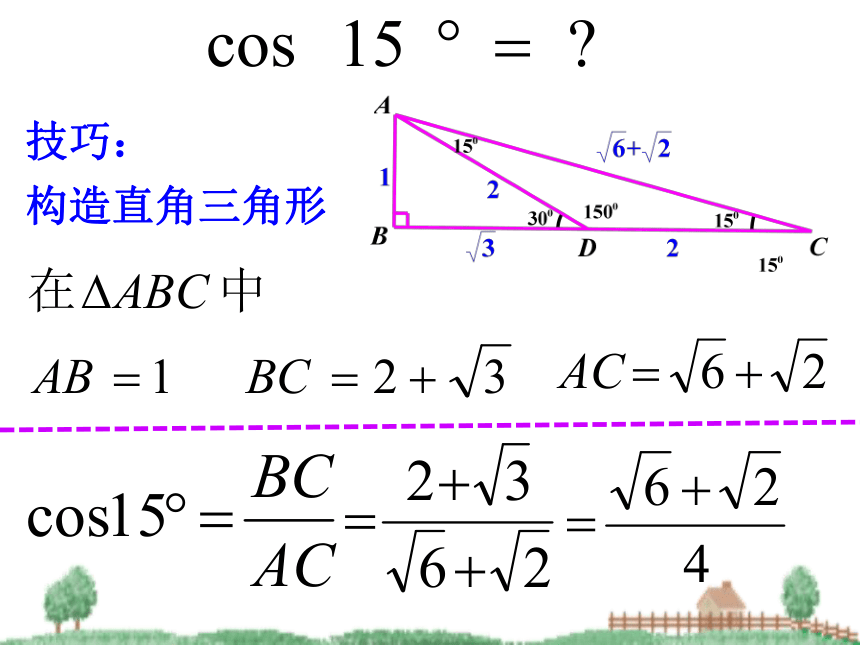
当电梯坡度为45度时,其他不变,等于多少?变式2:当电梯坡度为15度时,此时又等于多少?技巧:
构造直角三角形
小组合作探究
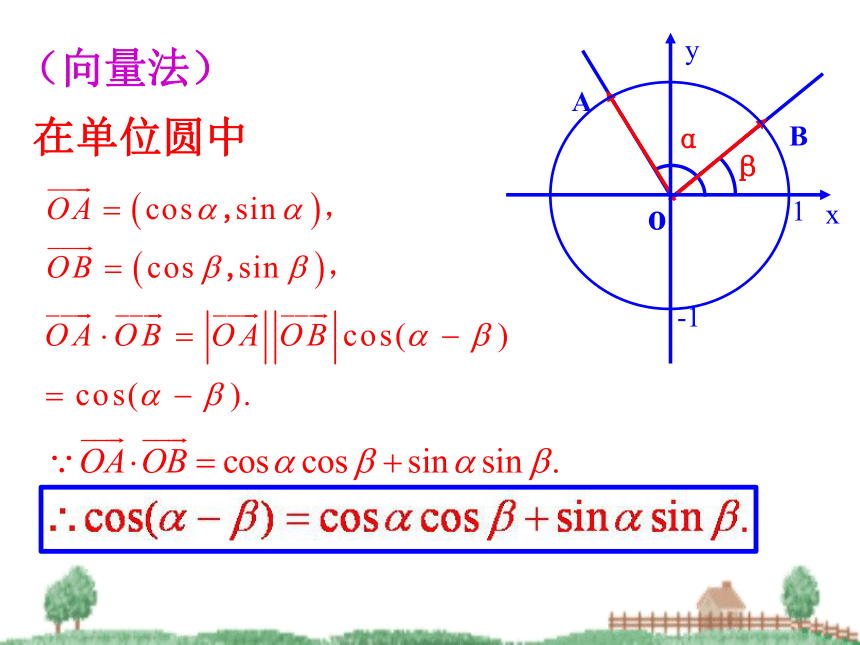
小组展示成果特殊值验证观察联想在单位圆中(向量法)称为差角的余弦公式说明: 1.公式中两边的符号正好相反.
2.公式右边同名三角函数相乘再相加,
且余弦在前正弦在后.两角差的余弦公式又可变换到同角三角函数公式:cos(α-β)=cosαcosβ+sinαsinβ 1.这堂课你学到了什么内容?如何学习的?
2.学习与应用过程中,你有什么体会?
课堂小结,回顾反思①学习了和差角余弦公式;
②假设猜想—反证否定—用向量探究公式
—证明结论—公式应用。①探究证明公式过程中,可以通过特殊情况去
讨论证明一般情况。也可以由一般去讨论特殊。
②公式应用中,可以有不同的解题方法。感 悟 G 波利亚: 在你证明一个定理之前,先猜想到这个定理;在你搞清楚证明细节之前,你必须猜想出证明的主导思想. 高斯:一个人在无结果地深思一个真理后,能够用迂回的方法证明它,并且最后找到了它的最简明而又自然的证法,那是极其令人高兴的。假如别人和我一样深刻和持续地思考数学真理,他会作出同样的发现。
感 悟布置作业,巩固提高
衷心祝愿同学们通过数学学习
变得更加聪明、更富有创造力!
当电梯坡度为45度时,其他不变,等于多少?变式2:当电梯坡度为15度时,此时又等于多少?技巧:
构造直角三角形
小组合作探究
小组展示成果特殊值验证观察联想在单位圆中(向量法)称为差角的余弦公式说明: 1.公式中两边的符号正好相反.
2.公式右边同名三角函数相乘再相加,
且余弦在前正弦在后.两角差的余弦公式又可变换到同角三角函数公式:cos(α-β)=cosαcosβ+sinαsinβ 1.这堂课你学到了什么内容?如何学习的?
2.学习与应用过程中,你有什么体会?
课堂小结,回顾反思①学习了和差角余弦公式;
②假设猜想—反证否定—用向量探究公式
—证明结论—公式应用。①探究证明公式过程中,可以通过特殊情况去
讨论证明一般情况。也可以由一般去讨论特殊。
②公式应用中,可以有不同的解题方法。感 悟 G 波利亚: 在你证明一个定理之前,先猜想到这个定理;在你搞清楚证明细节之前,你必须猜想出证明的主导思想. 高斯:一个人在无结果地深思一个真理后,能够用迂回的方法证明它,并且最后找到了它的最简明而又自然的证法,那是极其令人高兴的。假如别人和我一样深刻和持续地思考数学真理,他会作出同样的发现。
感 悟布置作业,巩固提高
衷心祝愿同学们通过数学学习
变得更加聪明、更富有创造力!
