人教版必修四1.1.4正弦函数的性质课件(21张)
文档属性
| 名称 | 人教版必修四1.1.4正弦函数的性质课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 413.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览


文档简介
课件21张PPT。正弦定理
(一)一、情景导入:
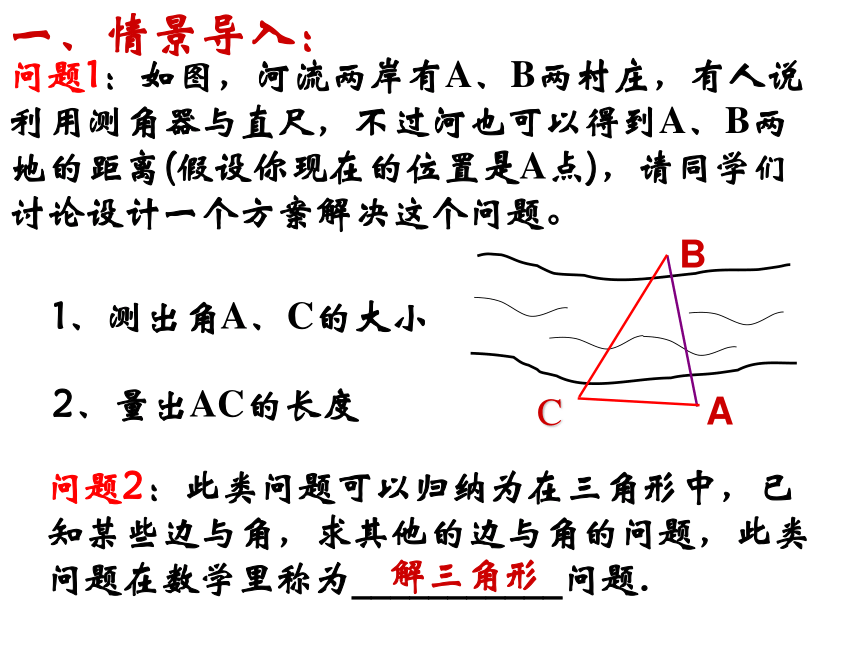
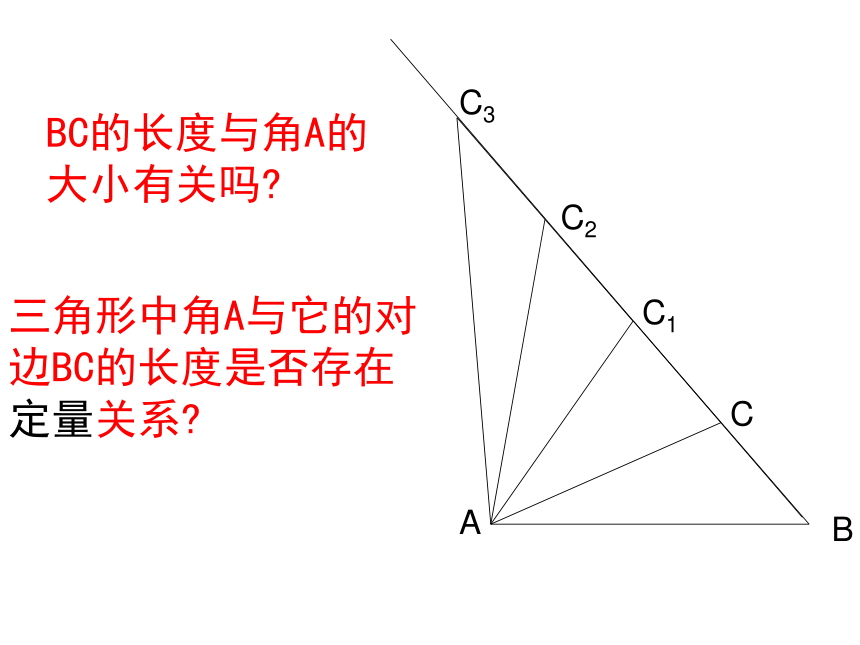
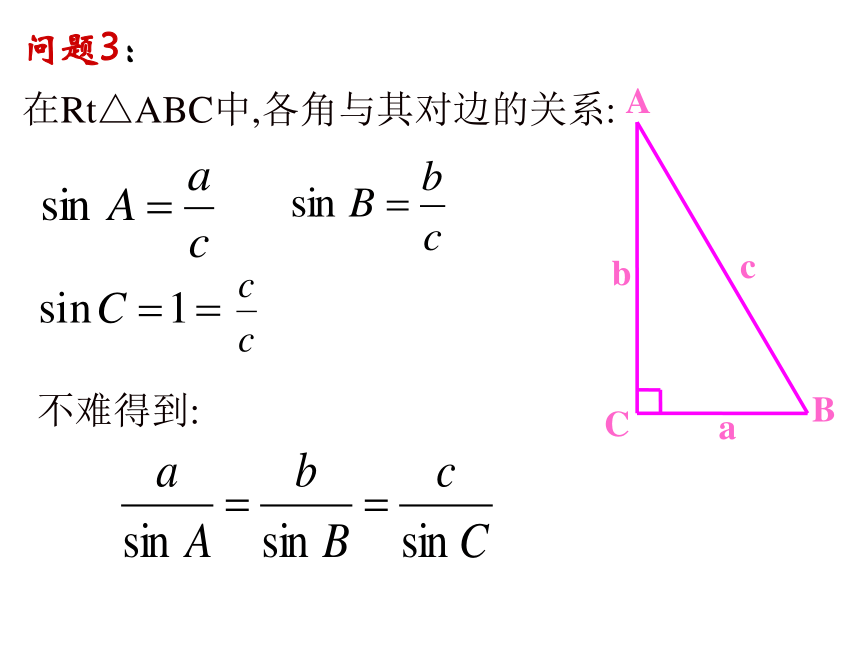
问题1:如图,河流两岸有A、B两村庄,有人说利用测角器与直尺,不过河也可以得到A、B两地的距离(假设你现在的位置是A点),请同学们讨论设计一个方案解决这个问题。问题2:此类问题可以归纳为在三角形中,已知某些边与角,求其他的边与角的问题,此类问题在数学里称为___________问题.解三角形C1、测出角A、C的大小2、量出AC的长度ABBC的长度与角A的大小有关吗?三角形中角A与它的对边BC的长度是否存在定量关系?问题3:在Rt△ABC中,各角与其对边的关系:
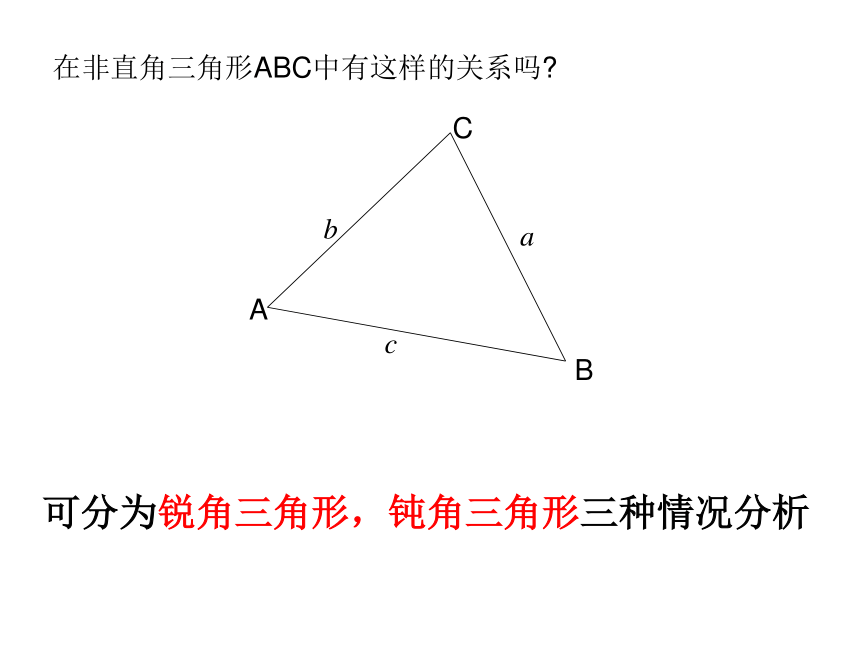
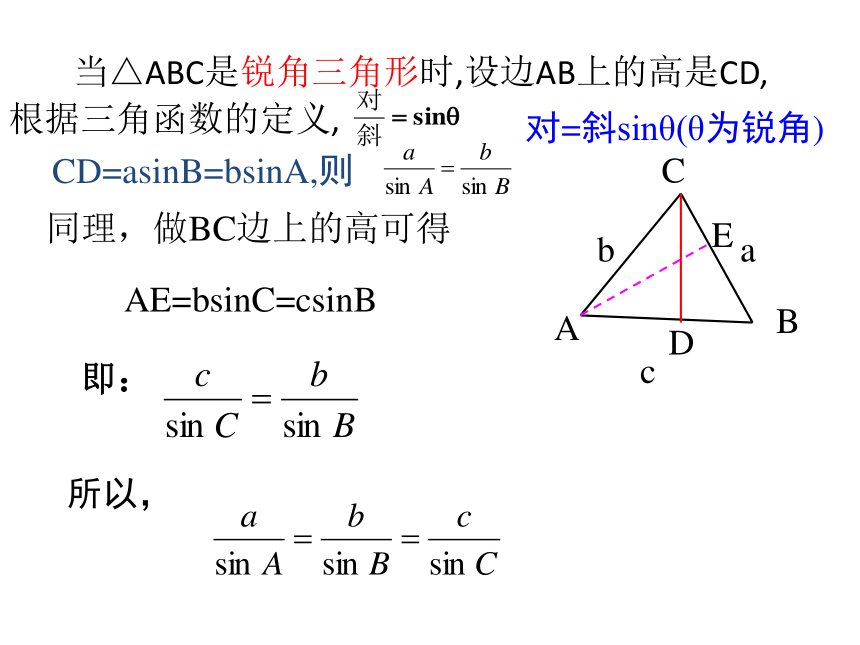
不难得到:在非直角三角形ABC中有这样的关系吗?可分为锐角三角形,钝角三角形三种情况分析. 当△ABC是锐角三角形时,设边AB上的高是CD,根据三角函数的定义, CABDabc同理,做BC边上的高可得
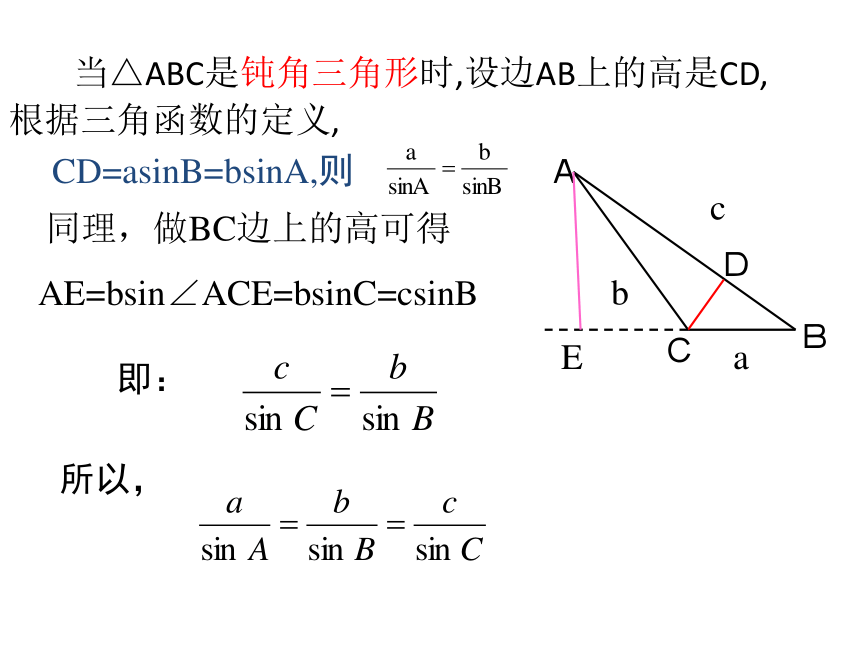
CD=asinB=bsinA,则E所以,AE=bsinC=csinB即:对=斜sinθ(θ为锐角) 当△ABC是钝角三角形时,设边AB上的高是CD,根据三角函数的定义, 同理,做BC边上的高可得
CD=asinB=bsinA,则所以,ABCDacbEAE=bsin∠ACE=bsinC=csinB即:在一个三角形中,各边和它所对角的
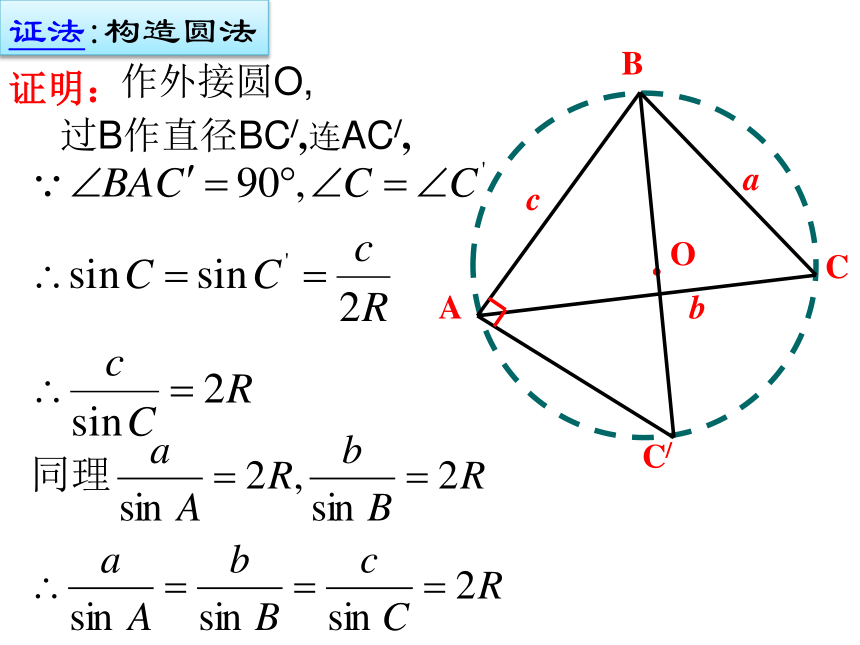
正弦的比相等.即正弦定理证明:作外接圆O,过B作直径BC/,连AC/,证法:构造圆法正弦定理可以解决三角形中哪类问题:① 已知两角和一边,求其他角和边. ②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.定理的应用例 1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01).解:已知两角和任意边,
求其他两边和一角a定理的应用1.在△ABC中,已知 A=75°,B= 45°,c=
求a , b.2.在△ABC中,已知 A=30°,B=120°,b=12
求a , c.练习例 2 已知a=16, b= , A=30° .
求角B,C和边c已知两边和其中一边
的对角,求其他边和角解:由正弦定理所以B=60°,或B=120°C=90°C=30°当B=120°时变式: a=30, b=26, A=30°求角B,C和边c
由于154.30 +300>1800故B只有一解 (如图)C=124.30,变式: a=30, b=26, A=30°求角B,C和边c
所以B=25.70,C=124.30,∵a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形 (1)b=13,a=26,B=30°.(2) b=40,c=20,C=45°.练习注:三角形中角的正弦值小于1时,角可能有两解无解(1)三角形常用公式:(2)正弦定理应用范围:① 已知两角和任意边,求其他两边和一角 ②
已知两边和其中一边的对角,求另一边
的对角。(注意解的情况)正弦定理:课堂小结已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考ACabab 一解判断满足下列的三角形的个数:
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o两解一解两解无解练习:
(一)一、情景导入:
问题1:如图,河流两岸有A、B两村庄,有人说利用测角器与直尺,不过河也可以得到A、B两地的距离(假设你现在的位置是A点),请同学们讨论设计一个方案解决这个问题。问题2:此类问题可以归纳为在三角形中,已知某些边与角,求其他的边与角的问题,此类问题在数学里称为___________问题.解三角形C1、测出角A、C的大小2、量出AC的长度ABBC的长度与角A的大小有关吗?三角形中角A与它的对边BC的长度是否存在定量关系?问题3:在Rt△ABC中,各角与其对边的关系:
不难得到:在非直角三角形ABC中有这样的关系吗?可分为锐角三角形,钝角三角形三种情况分析. 当△ABC是锐角三角形时,设边AB上的高是CD,根据三角函数的定义, CABDabc同理,做BC边上的高可得
CD=asinB=bsinA,则E所以,AE=bsinC=csinB即:对=斜sinθ(θ为锐角) 当△ABC是钝角三角形时,设边AB上的高是CD,根据三角函数的定义, 同理,做BC边上的高可得
CD=asinB=bsinA,则所以,ABCDacbEAE=bsin∠ACE=bsinC=csinB即:在一个三角形中,各边和它所对角的
正弦的比相等.即正弦定理证明:作外接圆O,过B作直径BC/,连AC/,证法:构造圆法正弦定理可以解决三角形中哪类问题:① 已知两角和一边,求其他角和边. ②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.定理的应用例 1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01).解:已知两角和任意边,
求其他两边和一角a定理的应用1.在△ABC中,已知 A=75°,B= 45°,c=
求a , b.2.在△ABC中,已知 A=30°,B=120°,b=12
求a , c.练习例 2 已知a=16, b= , A=30° .
求角B,C和边c已知两边和其中一边
的对角,求其他边和角解:由正弦定理所以B=60°,或B=120°C=90°C=30°当B=120°时变式: a=30, b=26, A=30°求角B,C和边c
由于154.30 +300>1800故B只有一解 (如图)C=124.30,变式: a=30, b=26, A=30°求角B,C和边c
所以B=25.70,C=124.30,∵a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形 (1)b=13,a=26,B=30°.(2) b=40,c=20,C=45°.练习注:三角形中角的正弦值小于1时,角可能有两解无解(1)三角形常用公式:(2)正弦定理应用范围:① 已知两角和任意边,求其他两边和一角 ②
已知两边和其中一边的对角,求另一边
的对角。(注意解的情况)正弦定理:课堂小结已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考ACaba
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o两解一解两解无解练习:
