6.5多边形的面积解决问题课件(18张ppt)
文档属性
| 名称 | 6.5多边形的面积解决问题课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览





文档简介
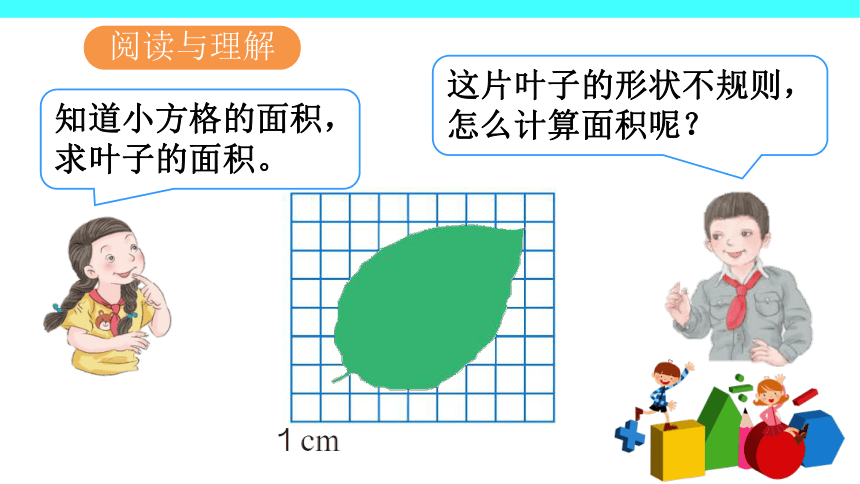
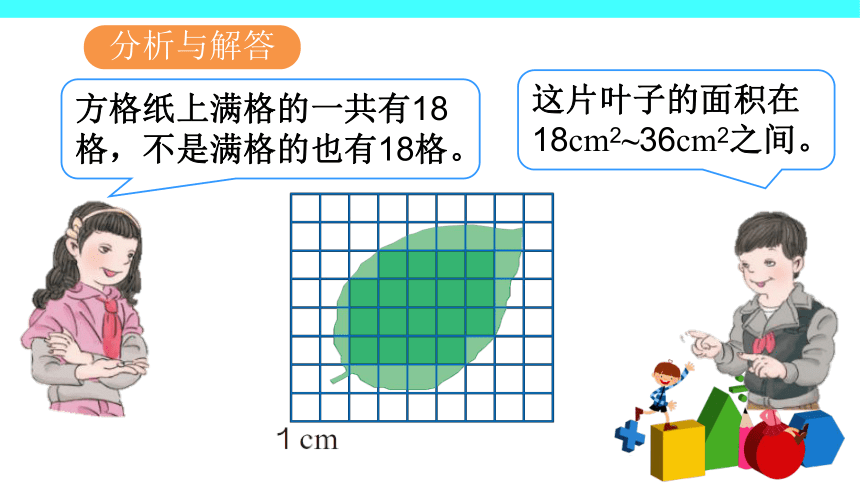
课件18张PPT。 不规则图形的面积多边形的面积3.能用所学知识解决日常生活中的简单问题,培养学生的应用意识。1.掌握参照规则图形面积估计不规则图形面积的方法。2.学习用数方格的方法计算不规则图形的面积,能估计不规则图形的面积大小,并能用不同方法灵活估算面积。学习目标学习重点学习难点将规则的简单图形和形似的不规则图形建立联系。掌握估算的方法和形成估算的习惯。一、情境导入我们已经会计算组合图形的面积了,那么生活中遇到不规则图形我们如何来估算它的面积呢?二、探究新知图中每个小方格的面积是1cm2 ,请你估计这片叶子的面积。知道小方格的面积,求叶子的面积。这片叶子的形状不规则,怎么计算面积呢?阅读与理解分析与解答方格纸上满格的一共有18格,不是满格的也有18格。这片叶子的面积在18cm2~36cm2之间。如果把不满一格的都按半格计算,这片叶子的面积大约是27cm2。我是将叶子的图形近似转化成平行四边形……S = ah
= 5×6
= 30(cm2 )因此,叶子的面积大约是30cm2。S = ab
= 5×6
= 30(cm2 )叶子的面积大约是30cm2。用转化的方法,将叶子的图形近似转化成长方形。 通过刚才的学习,今后我们再遇到不规则的图形,我们可以怎样估计它的面积呢?不规则的图形可以转化为学过的图形进行估算。先通过数方格确定图形面积的范围,再估算图形的面积。回顾与反思三、巩固提高1.图中每个小方格的面积为1m2,计算阴影部分面积。三角形 + 梯形 5×4÷2 + (5+2)×4÷2
= 24(m2) 近似转化成长方形 8×4 = 32(m2) 阴影部分面积大约是 32m2。 2.图中每个小方格的面积为1m2,请你估计这个池塘的面积。S =ab
=12×8
=96(m2 )这个池塘的面积大约是96m2。四、课堂小结不规则图形的面积估算数方格的方法进行估算把不规则的图形转化为学过的图形进行估算1.从课后习题中选取;
2.完成练习册本课时的习题。五、课后作业六、教学反思 通过创设情境,在生活中寻找学习素材,激发学生学习兴趣,体会数学与生活的紧密联系。为学生创设一个宽松、和谐、自主的学习氛围,在有趣的情境中引导学生积极主动地投入到探究问题中去,留给学生充分的时间和空间,并让学生在自己动手、动脑的基础上,引导学生交流、验证自己的想法,看一看自己没想到的方法有哪些,根据自己的能力有选择地学习其他方法。这样有序地学习,不仅拓展了学生的思维能力,还提高了学生的素质。
= 5×6
= 30(cm2 )因此,叶子的面积大约是30cm2。S = ab
= 5×6
= 30(cm2 )叶子的面积大约是30cm2。用转化的方法,将叶子的图形近似转化成长方形。 通过刚才的学习,今后我们再遇到不规则的图形,我们可以怎样估计它的面积呢?不规则的图形可以转化为学过的图形进行估算。先通过数方格确定图形面积的范围,再估算图形的面积。回顾与反思三、巩固提高1.图中每个小方格的面积为1m2,计算阴影部分面积。三角形 + 梯形 5×4÷2 + (5+2)×4÷2
= 24(m2) 近似转化成长方形 8×4 = 32(m2) 阴影部分面积大约是 32m2。 2.图中每个小方格的面积为1m2,请你估计这个池塘的面积。S =ab
=12×8
=96(m2 )这个池塘的面积大约是96m2。四、课堂小结不规则图形的面积估算数方格的方法进行估算把不规则的图形转化为学过的图形进行估算1.从课后习题中选取;
2.完成练习册本课时的习题。五、课后作业六、教学反思 通过创设情境,在生活中寻找学习素材,激发学生学习兴趣,体会数学与生活的紧密联系。为学生创设一个宽松、和谐、自主的学习氛围,在有趣的情境中引导学生积极主动地投入到探究问题中去,留给学生充分的时间和空间,并让学生在自己动手、动脑的基础上,引导学生交流、验证自己的想法,看一看自己没想到的方法有哪些,根据自己的能力有选择地学习其他方法。这样有序地学习,不仅拓展了学生的思维能力,还提高了学生的素质。
