人教版必修五1.1.2应用举例——测量两点间的距离课件(22张)
文档属性
| 名称 | 人教版必修五1.1.2应用举例——测量两点间的距离课件(22张) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览




文档简介
课件22张PPT。
余弦定理
正弦定理一、复习回顾AAS, ASA SSASSS, SAS问题1
正弦定理,余弦定理及其推论的表达形式是什么?问题2
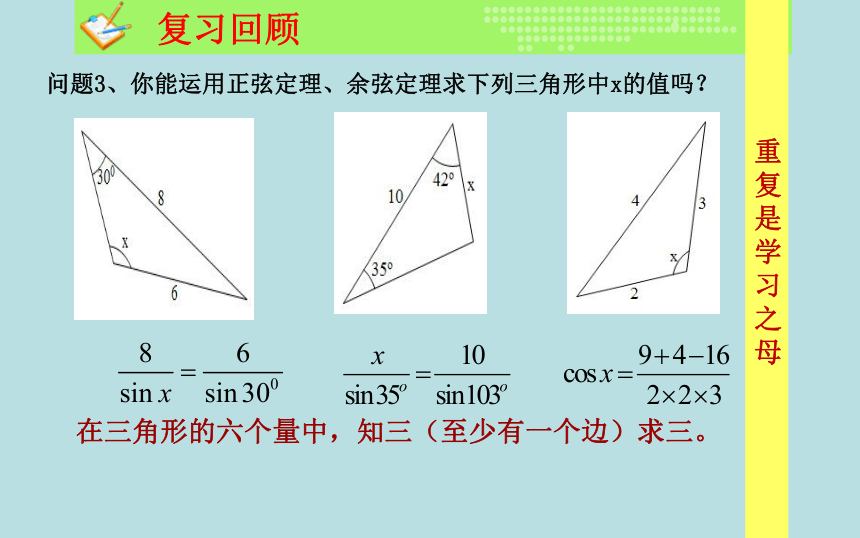
解三角形时,如何正确选择正弦定理或余弦定理?问题3、你能运用正弦定理、余弦定理求下列三角形中x的值吗?在三角形的六个量中,知三(至少有一个边)求三。
重复是学习之母
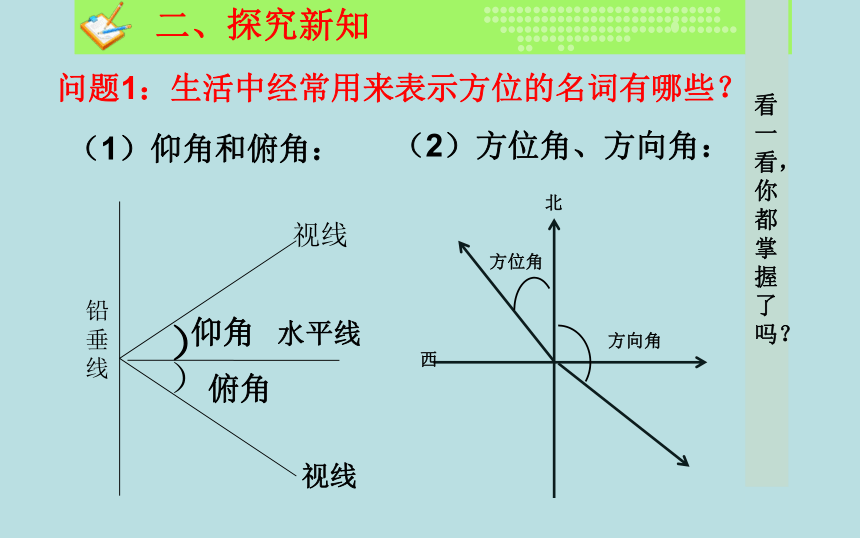
复习回顾二、探究新知问题1:生活中经常用来表示方位的名词有哪些?(1)仰角和俯角: (2)方位角、方向角:
看一看,你都掌握了吗?
方向角方位角北西经纬仪,测量水平角和竖直角的仪器。
是根据测角原理设计的。目前最常用
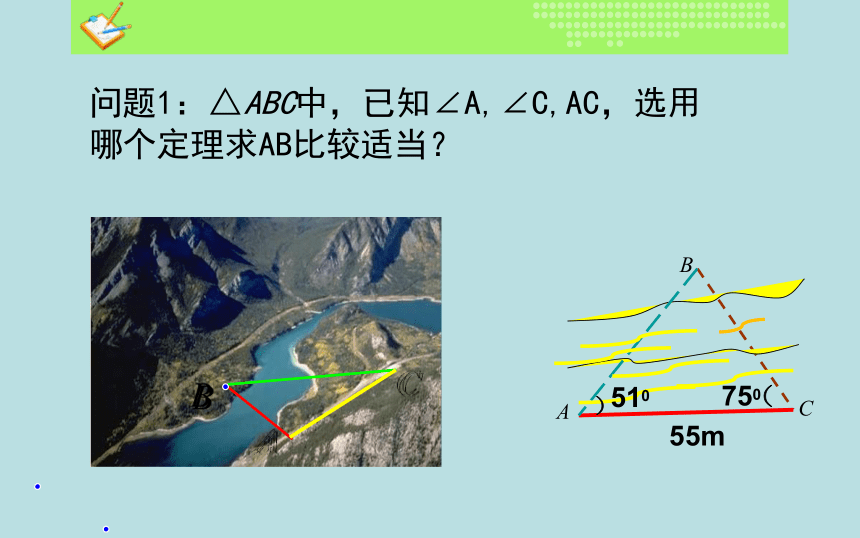
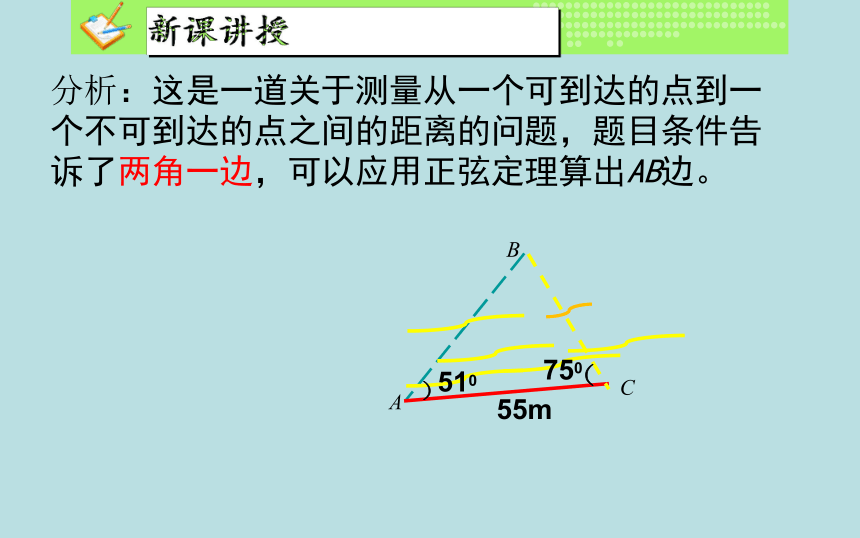
的是光学经纬仪。问题2、生活中常用的测量仪器有哪些?测角仪卷尺例1 如图,设A、B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m, ∠BAC=51°,∠ACB=75°.求A、B两点的距离(精确到0.1m).例题与变式问题:如何应用正弦定理和余弦定理求两点间的距离?问题1、怎样测量从一个可到达的点A到一个不可到达的点B之间的距离?三、新课讲授问题1:△ABC中,已知∠A,∠C,AC,选用哪个定理求AB比较适当?分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了两角一边,可以应用正弦定理算出AB边。解:根据正弦定理,得答:A、B两点间的距离约为65.7米。小结:测量从一个可到达的点A到一个不可到达的点B之间的距离的步骤有哪些?变式训练1.问题2 怎样测量两个不可到达的点之间的距离?变式训练2 在一次反恐作战战前准备中,为了弄清基地组织两个训练营地A和B之间的距离,盟军在两个相距为a的观测点C和D处,测得∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示.求基地组织的这两个训练营地A、B之间的距离.[分析] 可将AB放在△ABC中来求,为此应先求出AC和BC,再用余弦定理求AB.方法小结1.测量从一个可到达的点A到一个不可到达的点B之间的距离问题.这实际上就是已知三角形两个角和一边解三角形的问题,用正弦定理就可解决.2、测量两个不可到达的点A,B之间的距离问题.首先用正弦定理把未知的BC和AC的距离问题转化为测量可到达的一点与不可到达的一点之间距离的问题.然后应用_余弦定理_把不可到达的两点A,B之间的距离转化为求三角形ABC(或三角形ADC)的边长问题。.1.目标检测2. 为了测量水田两侧A,B两点间的距离(如图所示),某观测者在A的同侧选定一点C,测得AC=8 m,∠BAC=30°,∠BCA=45°,求A,B两点间的距离.1. 郑州市某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=7米,BC=5米,AC=8米,∠C=∠D.求AB的长度.配餐作业2. 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40 m,求电视塔的高度.
余弦定理
正弦定理一、复习回顾AAS, ASA SSASSS, SAS问题1
正弦定理,余弦定理及其推论的表达形式是什么?问题2
解三角形时,如何正确选择正弦定理或余弦定理?问题3、你能运用正弦定理、余弦定理求下列三角形中x的值吗?在三角形的六个量中,知三(至少有一个边)求三。
重复是学习之母
复习回顾二、探究新知问题1:生活中经常用来表示方位的名词有哪些?(1)仰角和俯角: (2)方位角、方向角:
看一看,你都掌握了吗?
方向角方位角北西经纬仪,测量水平角和竖直角的仪器。
是根据测角原理设计的。目前最常用
的是光学经纬仪。问题2、生活中常用的测量仪器有哪些?测角仪卷尺例1 如图,设A、B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m, ∠BAC=51°,∠ACB=75°.求A、B两点的距离(精确到0.1m).例题与变式问题:如何应用正弦定理和余弦定理求两点间的距离?问题1、怎样测量从一个可到达的点A到一个不可到达的点B之间的距离?三、新课讲授问题1:△ABC中,已知∠A,∠C,AC,选用哪个定理求AB比较适当?分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了两角一边,可以应用正弦定理算出AB边。解:根据正弦定理,得答:A、B两点间的距离约为65.7米。小结:测量从一个可到达的点A到一个不可到达的点B之间的距离的步骤有哪些?变式训练1.问题2 怎样测量两个不可到达的点之间的距离?变式训练2 在一次反恐作战战前准备中,为了弄清基地组织两个训练营地A和B之间的距离,盟军在两个相距为a的观测点C和D处,测得∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示.求基地组织的这两个训练营地A、B之间的距离.[分析] 可将AB放在△ABC中来求,为此应先求出AC和BC,再用余弦定理求AB.方法小结1.测量从一个可到达的点A到一个不可到达的点B之间的距离问题.这实际上就是已知三角形两个角和一边解三角形的问题,用正弦定理就可解决.2、测量两个不可到达的点A,B之间的距离问题.首先用正弦定理把未知的BC和AC的距离问题转化为测量可到达的一点与不可到达的一点之间距离的问题.然后应用_余弦定理_把不可到达的两点A,B之间的距离转化为求三角形ABC(或三角形ADC)的边长问题。.1.目标检测2. 为了测量水田两侧A,B两点间的距离(如图所示),某观测者在A的同侧选定一点C,测得AC=8 m,∠BAC=30°,∠BCA=45°,求A,B两点间的距离.1. 郑州市某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=7米,BC=5米,AC=8米,∠C=∠D.求AB的长度.配餐作业2. 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40 m,求电视塔的高度.
