人教版必修五第一单元解三角形复习课课件(40张)
文档属性
| 名称 | 人教版必修五第一单元解三角形复习课课件(40张) |

|
|
| 格式 | zip | ||
| 文件大小 | 479.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览










文档简介
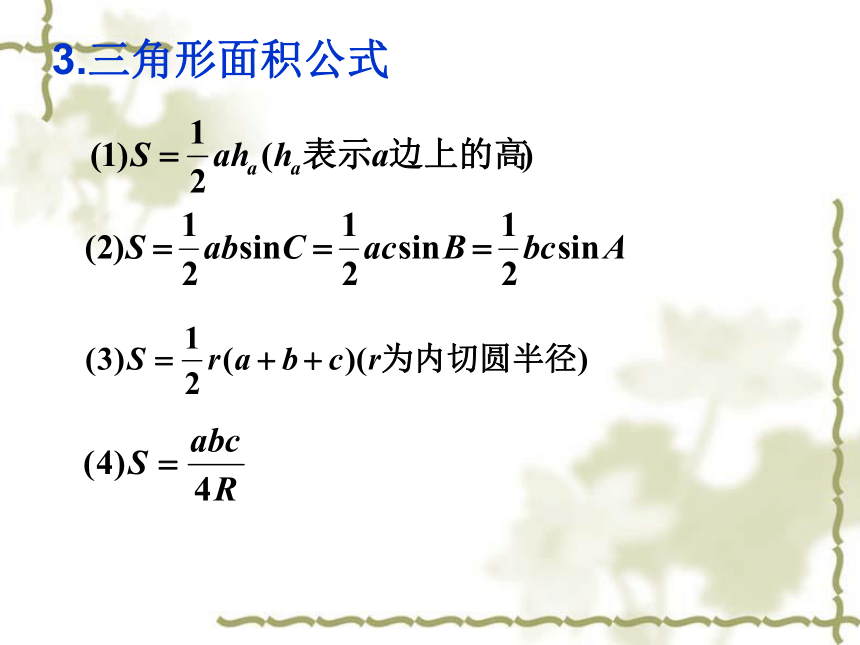
课件40张PPT。解三角形知识点梳理1.正弦定理正弦定理的变形:2.余弦定理余弦定理的变形:3.三角形面积公式4.三角形中的常见结论(2)在三角形中大边对大角,大角对大边.(3)任意两边之和大于第三边,任意两边之差小于第三边(4)有关三角形内角的三角函数式 中,A、B、C成等差数列的充要条件
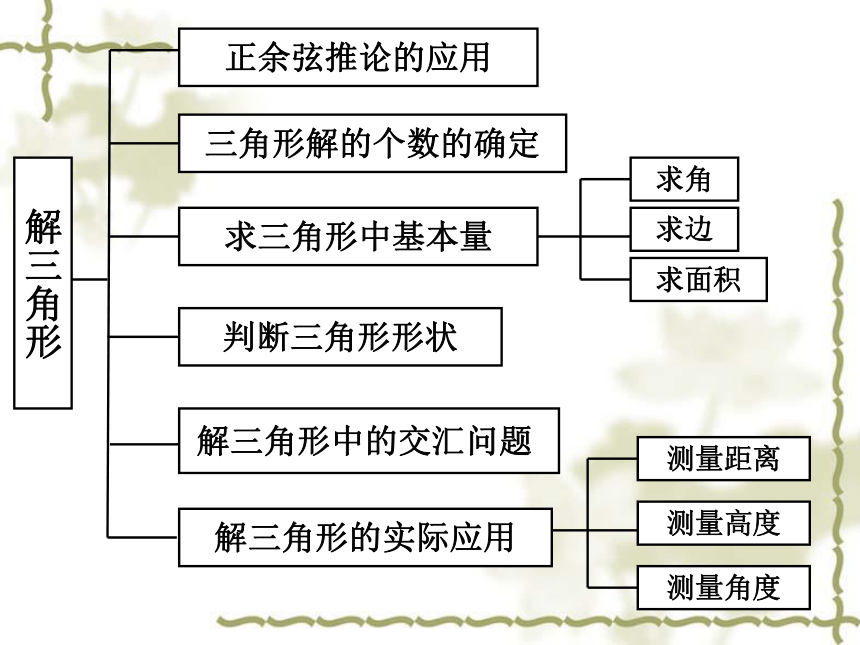
是B=60解三角形正余弦推论的应用三角形解的个数的确定求三角形中基本量判断三角形形状解三角形的实际应用求角求边求面积测量距离测量高度测量角度解三角形中的交汇问题 一、正余弦定理推论的应用二、三角形解的个数的确定解斜三角形有下表所示的四种情况:在已知a、b、A时判断三角形解的个数有三种方法:(2)用正弦定理确定另一边的对角(1)几何作图法(3)利用余弦定理整理后是以c为未知数的一元二次方程。因为c是三角形的边长,必有c>0。所以,所给定的三角形的解就取决于满足方程的未知数c正实数值得存在情况在三角形中,已知a、b和A时解的情况如下:例4.根据下列条件,判定三角形解的情况.解法一:(几何作图法)分别如下图①、②、③Ac点评:可通过正弦定理或几何作图很容易看出三角形有一个解的情况有两种。这些有些同学容易出现误区,直接令关于C的一元二次方程有一解,很容易少考虑a>b的情况,以后做题时要注意。三、求三角形基本量 求三角形基本量包括求三角形的内角、求三角形的边、求三角形的面积这三类。在求基本量时运用正余弦定理以及它们的推论利用已知条件进行边角互化后求出未知量。在进行求解过程中往往会与三角恒等变换知识结合,同时要注意在解出结果后运用第二部分所讲的三角形解的个数的判定来对结果进行取舍,得到最终结果。求三角形的角求三角形的边点评:此类问题求解需要主要解的个数的讨论,比较上述两种解法,解法二比较简便。求三角形的面积四、判断三角形形状判定三角形形状通常有两种途径:化边为角;化角为边具体有如下四种方法:
①通过正弦定理实施边角转换;
②通过余弦定理实施边角转换;
③通过三角变换找出角之间的关系;
④通过三角函数符号的判断及正余弦函数有界性的 讨论已知边之间的关系总结:解法一是用正弦定理将边关系转化成角的关系,运用三角变换找出角之间的关系;解法二用余弦定理直接运用边的关系判断形状;已知角的三角函数的关系等腰解:已知边与角之间的关系总结:根据已知条件,适当选取适用的定理,进行边角互化结合三角变换找出三边之间的关系或者是找出内角之间的关系来判断形状。五、解三角形中的交汇问题 在知识交汇处命题是高考考查的热点,体现了多考一点“想”,少考一点“算”的理念,所以挖掘知识内的交汇是学习中的重点。解三角形与其它知识的交汇体现与向量、三角函数、三角变换、数列、、解析几何、立体几何等几个方面知识的结合。点评:此题结合向量、三角变换的知识同时运用余弦定理和三角形面积。三角变换和向量与解三角形的结合是高考的重点,同时考察学生多方面的知识。点评:此题运用三角形面积公式推出了角平分线定理。在立体几何中也经常用到解三角形,立体几何中一般都是求三角形的基本量,这里不再给出例题。六、解三角形在生活中的应用1.解三角形在生活中应用非常广泛,如测量、航海、物理 几何等方面都要用到解三角形的知识.这些实际问题基本上分成测量长度、高度、角度三种类型.解三角形应用题得一般步骤及基本思路.
(1)一般步骤:
①分析:理解题意,分清已知与未知,画出示意图;
②建模:根据已知条件与求解目标,把一直亮与求解量尽量集中在有关的三角形总,建立一个解三角形的数学模型;
③求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;(2)基本思路:实际问题数学模型数学模型的解实际问题的解2.实际问题中的有关术语、名称
(1)仰角和俯角 在视线和水平线所成的较重,视线在水平线上方的角角仰角,在水平线下方的角俯角(如下图).仰角俯角 ④检验:检验上述所求的结果是否具有实际意义从而得出实际问题的解.(2)方位角 从正北方向顺时针转到目标方向线的夹角,如B点的方位角为α(如下图①)(3)方向角
①正南方向:从原点O出发的经过目标射线与正南的方向线重合,即目标在正南的方向线上.依次可类推正北方向、正东方向和正西方向.②东南方向:指经过目标的涉嫌是正东和正南的夹角平分线(如图②).
③北偏东α:从正北向正东方向旋转α角度(图③)
④南偏西β:从正南向正西方向旋转β角度(图④)
作业
是B=60解三角形正余弦推论的应用三角形解的个数的确定求三角形中基本量判断三角形形状解三角形的实际应用求角求边求面积测量距离测量高度测量角度解三角形中的交汇问题 一、正余弦定理推论的应用二、三角形解的个数的确定解斜三角形有下表所示的四种情况:在已知a、b、A时判断三角形解的个数有三种方法:(2)用正弦定理确定另一边的对角(1)几何作图法(3)利用余弦定理整理后是以c为未知数的一元二次方程。因为c是三角形的边长,必有c>0。所以,所给定的三角形的解就取决于满足方程的未知数c正实数值得存在情况在三角形中,已知a、b和A时解的情况如下:例4.根据下列条件,判定三角形解的情况.解法一:(几何作图法)分别如下图①、②、③Ac点评:可通过正弦定理或几何作图很容易看出三角形有一个解的情况有两种。这些有些同学容易出现误区,直接令关于C的一元二次方程有一解,很容易少考虑a>b的情况,以后做题时要注意。三、求三角形基本量 求三角形基本量包括求三角形的内角、求三角形的边、求三角形的面积这三类。在求基本量时运用正余弦定理以及它们的推论利用已知条件进行边角互化后求出未知量。在进行求解过程中往往会与三角恒等变换知识结合,同时要注意在解出结果后运用第二部分所讲的三角形解的个数的判定来对结果进行取舍,得到最终结果。求三角形的角求三角形的边点评:此类问题求解需要主要解的个数的讨论,比较上述两种解法,解法二比较简便。求三角形的面积四、判断三角形形状判定三角形形状通常有两种途径:化边为角;化角为边具体有如下四种方法:
①通过正弦定理实施边角转换;
②通过余弦定理实施边角转换;
③通过三角变换找出角之间的关系;
④通过三角函数符号的判断及正余弦函数有界性的 讨论已知边之间的关系总结:解法一是用正弦定理将边关系转化成角的关系,运用三角变换找出角之间的关系;解法二用余弦定理直接运用边的关系判断形状;已知角的三角函数的关系等腰解:已知边与角之间的关系总结:根据已知条件,适当选取适用的定理,进行边角互化结合三角变换找出三边之间的关系或者是找出内角之间的关系来判断形状。五、解三角形中的交汇问题 在知识交汇处命题是高考考查的热点,体现了多考一点“想”,少考一点“算”的理念,所以挖掘知识内的交汇是学习中的重点。解三角形与其它知识的交汇体现与向量、三角函数、三角变换、数列、、解析几何、立体几何等几个方面知识的结合。点评:此题结合向量、三角变换的知识同时运用余弦定理和三角形面积。三角变换和向量与解三角形的结合是高考的重点,同时考察学生多方面的知识。点评:此题运用三角形面积公式推出了角平分线定理。在立体几何中也经常用到解三角形,立体几何中一般都是求三角形的基本量,这里不再给出例题。六、解三角形在生活中的应用1.解三角形在生活中应用非常广泛,如测量、航海、物理 几何等方面都要用到解三角形的知识.这些实际问题基本上分成测量长度、高度、角度三种类型.解三角形应用题得一般步骤及基本思路.
(1)一般步骤:
①分析:理解题意,分清已知与未知,画出示意图;
②建模:根据已知条件与求解目标,把一直亮与求解量尽量集中在有关的三角形总,建立一个解三角形的数学模型;
③求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;(2)基本思路:实际问题数学模型数学模型的解实际问题的解2.实际问题中的有关术语、名称
(1)仰角和俯角 在视线和水平线所成的较重,视线在水平线上方的角角仰角,在水平线下方的角俯角(如下图).仰角俯角 ④检验:检验上述所求的结果是否具有实际意义从而得出实际问题的解.(2)方位角 从正北方向顺时针转到目标方向线的夹角,如B点的方位角为α(如下图①)(3)方向角
①正南方向:从原点O出发的经过目标射线与正南的方向线重合,即目标在正南的方向线上.依次可类推正北方向、正东方向和正西方向.②东南方向:指经过目标的涉嫌是正东和正南的夹角平分线(如图②).
③北偏东α:从正北向正东方向旋转α角度(图③)
④南偏西β:从正南向正西方向旋转β角度(图④)
作业
