人教版必修五3.3.3简单的线性规划问题课件(16张)
文档属性
| 名称 | 人教版必修五3.3.3简单的线性规划问题课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 206.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览




文档简介
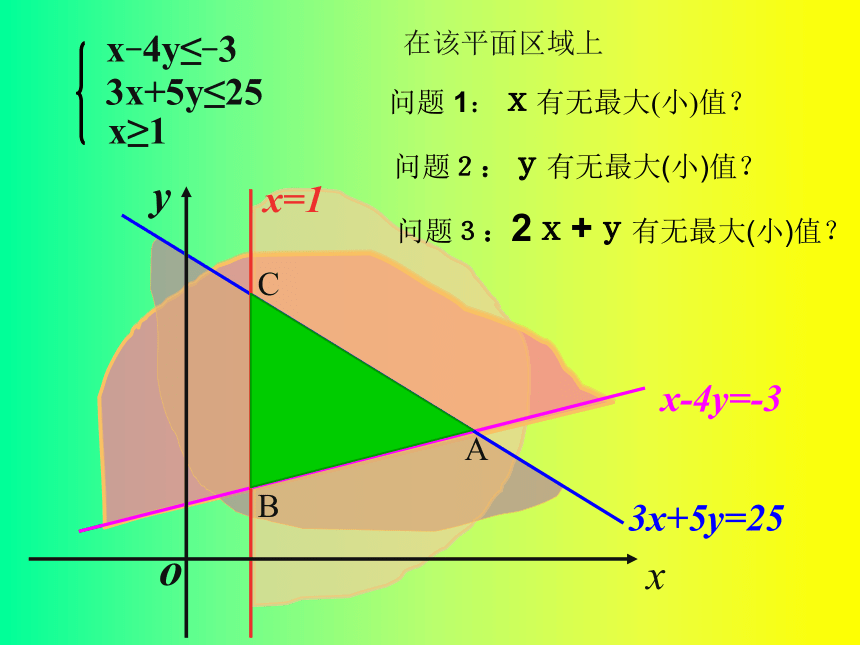
课件16张PPT。简单线性规划CB练习:画出不等式组 表示的平面区域。3x+5y≤ 25 x -4y≤ - 3x≥1问题:3x+5y≤25x-4y≤-3x≥1问题2:y有无最大(小)值?xyo问题3:2x+y有无最大(小)值?xyox=1CB 设z=2x+y,式中变量x、y满足下列条件 ,
求z的最大值和最小值。
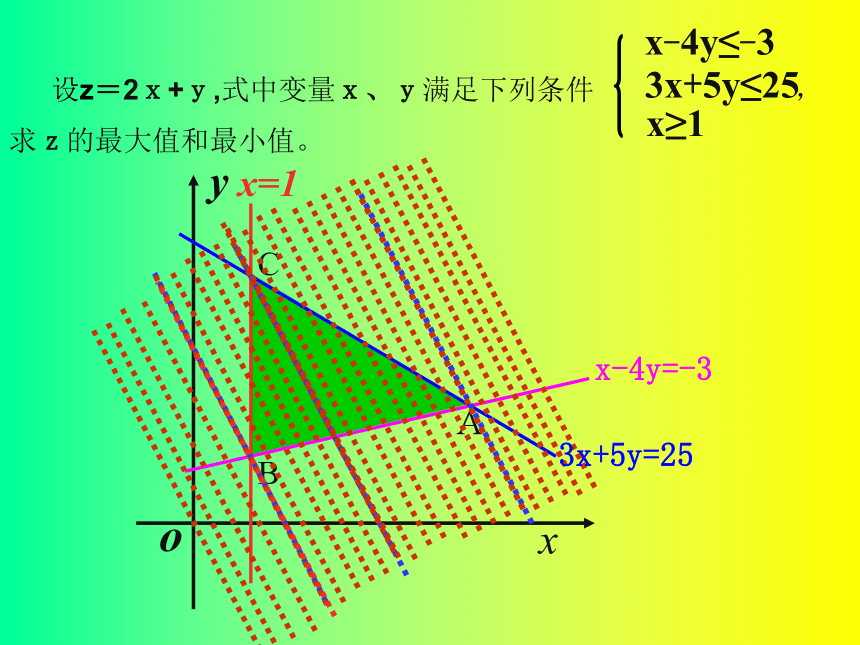
3x+5y≤25x-4y≤-3x≥1Ax-4y=-33x+5y=25xyox-4y=-3x=1C 设z=2x+y,式中变量x、y满足下列条件 ,
求z的最大值和最小值。 BA3x+5y=25问题 1: 将z=2x+y变形?问题 2: z几何意义是_____________________________。斜率为-2的直线在y轴上的截距 则直线 l:
2x+y=z是一簇与 l0平行的直线,故
直线 l 可通过平移直线l0而得,当直
线往右上方平移时z 逐渐增大:
当l 过点 B(1,1)时,z 最小,即zmin=3
当l 过点A(5,2)时,z最大,即
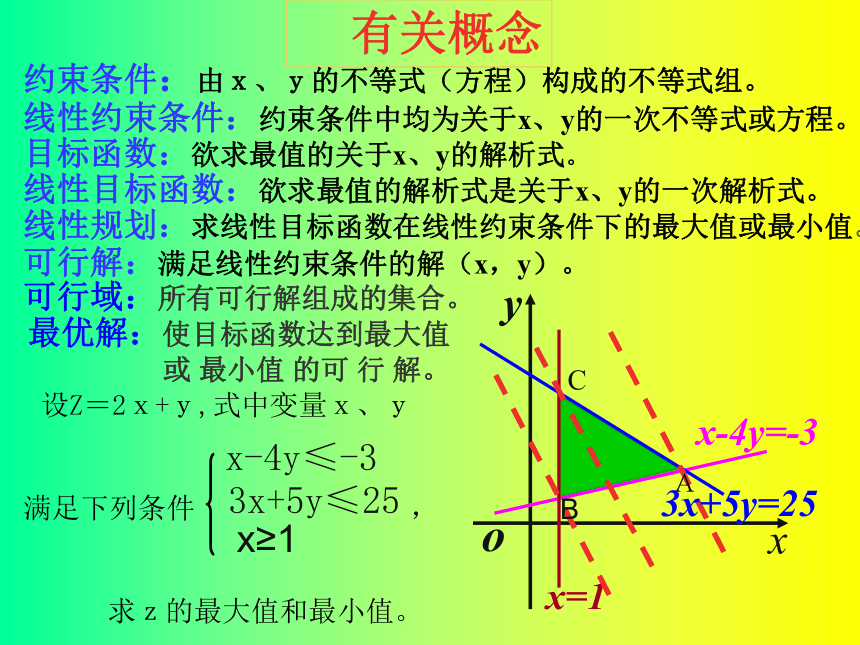
zmax=2×5+2=12 。 析: 作直线l0 :2x+y=0 ,最优解:使目标函数达到最大值或 最小值 的可 行 解。 线性约束条件:约束条件中均为关于x、y的一次不等式或方程。有关概念 约束条件:由x、y的不等式(方程)构成的不等式组。目标函数:欲求最值的关于x、y的解析式。线性目标函数:欲求最值的解析式是关于x、y的一次解析式。线性规划:求线性目标函数在线性约束条件下的最大值或最小值。可行解:满足线性约束条件的解(x,y)。 可行域:所有可行解组成的集合。xyox-4y=-3x=1CBA3x+5y=25 设Z=2x+y,式中变量x、y
满足下列条件 ,
求z的最大值和最小值。
例1:设z=2x-y,式中变量x、y满足下列条件
求z的最大值和最小值。解:作出可行域如图:由z=2x-y得y=2x-z当z=0时,设直线 l0:y=2x 当l0经过可行域上点A时,
-z 最小,即z最大。 当l0经过可行域上点C时,
-z最大,即z最小。∴ zmax=2×5-2=8 zmin=2×1-4.4= -2.4(5,2)(1,4.4)平移l0,平移l0 ,2x-y=0解线性规划问题的步骤: 2、 在线性目标函数所表示的一组平行线
中,用平移的方法找出与可行域中的
点(最优解)使纵截距最大或最小的直线; 3、 通过解方程组求出最优解与目标函数的最大(小)值; 4、 作出答案。 1、 画出线性约束条件所表示的可行域;画移求答3x+5y=25 例2:已知x、y满足 ,设z=ax+y (a>0), 若z
取得最大值时,对应点有无数个,求a 的值。xyox-4y=-3x=1CBA解:当直线 l :y =-ax+ z 与直线重合时,有无数个点,使函数值取得最大值,此时有: k l =kAC k l = -a例3:某工厂生产甲、乙两种产品.已知生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t.甲、乙两种产品应各生产多少(精确到0.1t),能使利润总额达到最大?产品消耗量资源分析:将已知数据列成下表解:设生产甲、乙两种产品分别为x(t)、y(t),利润总和为z元,根据题意得:
例3:满足线性约束条件 的可行域中共有
多少个整数解。1223314455xy0解:由题意得可行域如图: 由图知满足约束条件的
可行域中的整点为(1,1)、
(1,2)、(2,1)、(2,2)
故有四个整点可行解.小结:
1.线性规划问题的有关概念;
2. 用图解法解线性规划问题的一般步骤;
3. 根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求出最优解;
求z的最大值和最小值。
3x+5y≤25x-4y≤-3x≥1Ax-4y=-33x+5y=25xyox-4y=-3x=1C 设z=2x+y,式中变量x、y满足下列条件 ,
求z的最大值和最小值。 BA3x+5y=25问题 1: 将z=2x+y变形?问题 2: z几何意义是_____________________________。斜率为-2的直线在y轴上的截距 则直线 l:
2x+y=z是一簇与 l0平行的直线,故
直线 l 可通过平移直线l0而得,当直
线往右上方平移时z 逐渐增大:
当l 过点 B(1,1)时,z 最小,即zmin=3
当l 过点A(5,2)时,z最大,即
zmax=2×5+2=12 。 析: 作直线l0 :2x+y=0 ,最优解:使目标函数达到最大值或 最小值 的可 行 解。 线性约束条件:约束条件中均为关于x、y的一次不等式或方程。有关概念 约束条件:由x、y的不等式(方程)构成的不等式组。目标函数:欲求最值的关于x、y的解析式。线性目标函数:欲求最值的解析式是关于x、y的一次解析式。线性规划:求线性目标函数在线性约束条件下的最大值或最小值。可行解:满足线性约束条件的解(x,y)。 可行域:所有可行解组成的集合。xyox-4y=-3x=1CBA3x+5y=25 设Z=2x+y,式中变量x、y
满足下列条件 ,
求z的最大值和最小值。
例1:设z=2x-y,式中变量x、y满足下列条件
求z的最大值和最小值。解:作出可行域如图:由z=2x-y得y=2x-z当z=0时,设直线 l0:y=2x 当l0经过可行域上点A时,
-z 最小,即z最大。 当l0经过可行域上点C时,
-z最大,即z最小。∴ zmax=2×5-2=8 zmin=2×1-4.4= -2.4(5,2)(1,4.4)平移l0,平移l0 ,2x-y=0解线性规划问题的步骤: 2、 在线性目标函数所表示的一组平行线
中,用平移的方法找出与可行域中的
点(最优解)使纵截距最大或最小的直线; 3、 通过解方程组求出最优解与目标函数的最大(小)值; 4、 作出答案。 1、 画出线性约束条件所表示的可行域;画移求答3x+5y=25 例2:已知x、y满足 ,设z=ax+y (a>0), 若z
取得最大值时,对应点有无数个,求a 的值。xyox-4y=-3x=1CBA解:当直线 l :y =-ax+ z 与直线重合时,有无数个点,使函数值取得最大值,此时有: k l =kAC k l = -a例3:某工厂生产甲、乙两种产品.已知生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t.甲、乙两种产品应各生产多少(精确到0.1t),能使利润总额达到最大?产品消耗量资源分析:将已知数据列成下表解:设生产甲、乙两种产品分别为x(t)、y(t),利润总和为z元,根据题意得:
例3:满足线性约束条件 的可行域中共有
多少个整数解。1223314455xy0解:由题意得可行域如图: 由图知满足约束条件的
可行域中的整点为(1,1)、
(1,2)、(2,1)、(2,2)
故有四个整点可行解.小结:
1.线性规划问题的有关概念;
2. 用图解法解线性规划问题的一般步骤;
3. 根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求出最优解;
