人教版选修1-1 1.1.2 四种命题课件(24张)
文档属性
| 名称 | 人教版选修1-1 1.1.2 四种命题课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 361.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览







文档简介
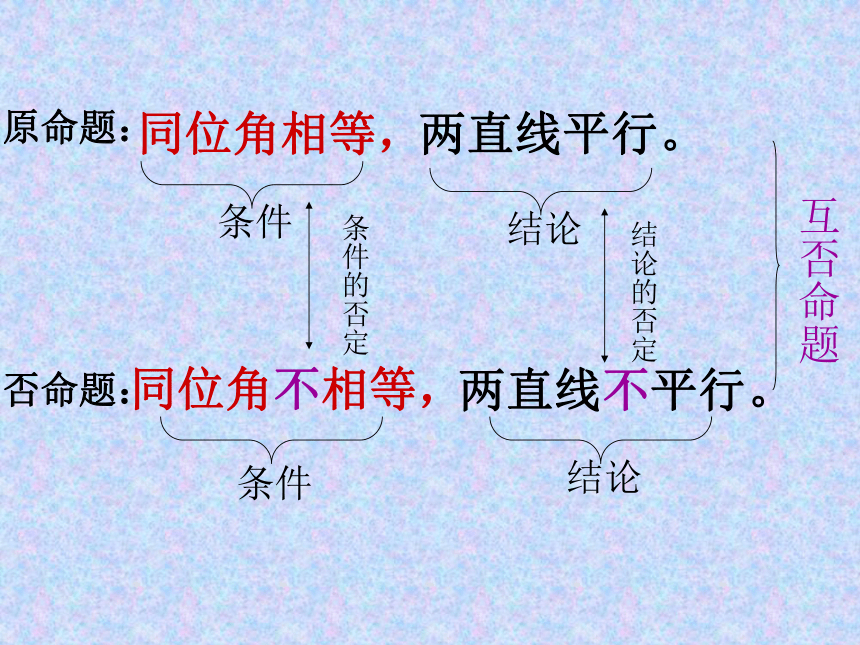
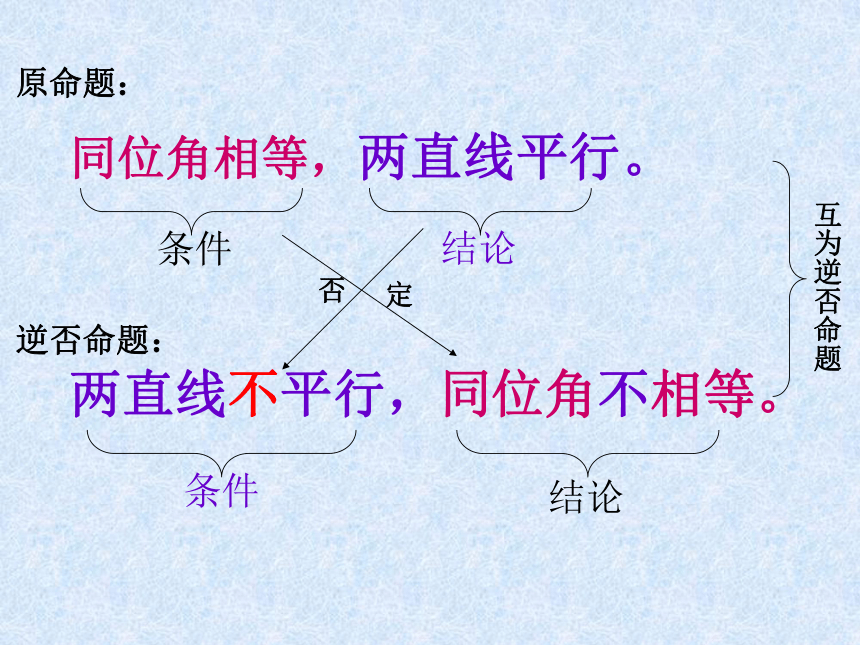
课件24张PPT。四种命题同位角相等,两直线平行。同位角不相等,两直线不平行。同位角相等,两直线平行。条件结论同位角不相等,两直线不平行。条件 结论条件的否定结论的否定互否命题原命题:否命题:同位角相等,两直线平行。两直线不平行,同位角不相等。同位角相等,两直线平行。两直线不平行,同位角不相等。条件结论结论条件否定 互为逆否命题原命题:逆否命题:同位角相等,两直线平行。两直线平行,同位角相等。同位角不相等,两直线不平行。两直线不平行,同位角不相等。原命题:逆命题:否命题:逆否命题:原命题:若P,则q.逆命题:否命题: 逆否命题:若q, 则p.若┐P ,则┐q。若┐q ,则┐P 。例1 把下列命题改写成“若P则q”的形式,并写出它们的逆命题、否命题与逆否命题:(1) 负数的平方是正数;
(2) 正方形的四条边相等,(1)负数的平方是正数。
解:原命题可以写成:若一个数是负数,则它的平方是正数。逆命题:若一个数的平方是正数,则它是负数。否命题:若一个数不是负数,则它的平方不是正数。逆否命题:若一个数的平方不是正数,则它不是负数。(2)正方形的四条边相等。解:原命题可以写成:若一个四边形是正方形,则它的四条边相等。逆命题:若一个四边形的四条边相等,则它是正方形。逆否命题:若一个四边形的四条边不相等,则它不是正方形。否命题:若一个四边形不是正方形,则它的四条边不相等。例2把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题。(1)末位是0的整数,可以被5整除;(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;(1)末位是0的整数,可以被5整除;解:原命题可以写成:若一个整数的末位是0,则它可以被5整除;逆命题:若一个整数可以被5整除,则它的末位是0。否命题:若一个整数的末位不是0,则它不可以被5整除。逆否命题:若一个整数不可以被5整除,则它的末位不是0。(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;解:原命题可以写成:若一点为线段的垂直平分线上的点,则它与这条线段两个端点的距离相等;逆命题:若一点与这条线段两个端点的距离相等,则此点在线段的垂直平分线上。否命题:若一点不为线段的垂直平分线上的点,则它与这条线段两个端点的距离不相等。逆否命题:若一点与这条线段两个端点的距离不相等,则此点不在线段的垂直平分线上。原命题
若p则q否命题
若┐p则┐q逆否命题
若┐q则┐p逆命题
若q则p互
否互 逆互 逆互
否互 为互 为逆 否逆 否写出下列命题的逆命题,并判断它们的真假:
(1)若X<Y,则Y>X
(2)若a=0,则ab=0(1)逆命题:若Y>X,则X<Y真命题(2)逆命题:若ab=0,则a=0假命题原命题为真,逆命题不一定为真写出下列命题的否命题,并判断它们的真假:
(1)若X<Y,则Y>X
(2)若a=0,则ab=0(1)否命题:若X≥Y,则Y≤X真命题(2)否命题:若a≠0,则ab≠0。假命题原命题为真,否命题不一定为真写出下列命题的逆否命题,并判断它们的真假:
(1)若X<Y,则Y>X
(2)若a=0,则ab= 0(1)逆否命题:若Y≤X,则X≥Y真命题(2)逆否命题:若ab≠0,则a ≠ 0真命题原命题为真,逆否命题为真。
例2: 设原命题是“当 c>0时,若 a > b ,则 a c > b c”,写出它的逆命题、否命题与逆否命题,并分别判断它们的真假:解:逆命题:当 c > 0时, 若 a c > b c , 则 a> b.逆命题为真.否命题:当 c> 0时,若 a ≤ b,则 a c ≤ b c.否命题为真.逆否命题:当 c > 0时,若 a c ≤ b c,则 a ≤ b.逆否命题为真.原命题为真互为逆否关系的两个命题同真假
其余关系的两个命题真假不一定相同原命题:例3:写出下列命题的否定与否命题
(1)正n边形(n≥3)的n个内角全相等
(2)末位数字是0 或5 的整数,能被5整除
(3)零的平方等于0
(4)平行四边形的对角线相等且互相平分解(1)命题的否定:正n边形(n≥3)的n个内角不全相等否命题:不是正n边形(n≥3)的n个内角不全相等(2)命题的否定:末位数字是0 或5 的整数,不能被5整除否命题:末位数字不是0也不是5的整数,不能被5整除(3)命题的否定:零的平方不等于0否命题:不等于零的数的平方不等于0(4)命题的否定:平行四边形的对角线不相等或不互相平分否命题:若四边形不是平行四边形,则它的对角线的对
角线不相等或不互相平分总结:1.写原命题的逆命题,否命题,逆否命题时关键是找出所给原命题的条件p 和结论 q2. 命题p 的否定与否命题
命题p 的否定即非p 只是否定命题 p 的结论
否命题是对原命题“若p 则q ”既否其条件又否其结论写出下列命题的否定及其否命题
(1)菱形的四条边都相等
(2)面积相等的三角形是全等三角形
(3)所有的等边三角形各角都相等
(4)所有的方程都不是不等式
(5)若a bc=0 ,则a, b, c中至少有一个为0
(6)有些质数是奇数
(7)若(x-1) (y+2)=0 ,则x=1或y=-2
(8)若 x2+y2 ≠ 0,则x ≠ 0或y ≠ 0填空:(1)命题”等式两边都乘以同一个数,所得结果仍是等式“的逆命题是___________________________________逆否命题是
____________________________________(2)命题“到圆心的距离不等于半径的直线不是圆的切线”的逆否命题是_____________________________________若一条直线是圆的切线,则它到圆心的距离等于半径。
(2) 正方形的四条边相等,(1)负数的平方是正数。
解:原命题可以写成:若一个数是负数,则它的平方是正数。逆命题:若一个数的平方是正数,则它是负数。否命题:若一个数不是负数,则它的平方不是正数。逆否命题:若一个数的平方不是正数,则它不是负数。(2)正方形的四条边相等。解:原命题可以写成:若一个四边形是正方形,则它的四条边相等。逆命题:若一个四边形的四条边相等,则它是正方形。逆否命题:若一个四边形的四条边不相等,则它不是正方形。否命题:若一个四边形不是正方形,则它的四条边不相等。例2把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题。(1)末位是0的整数,可以被5整除;(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;(1)末位是0的整数,可以被5整除;解:原命题可以写成:若一个整数的末位是0,则它可以被5整除;逆命题:若一个整数可以被5整除,则它的末位是0。否命题:若一个整数的末位不是0,则它不可以被5整除。逆否命题:若一个整数不可以被5整除,则它的末位不是0。(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;解:原命题可以写成:若一点为线段的垂直平分线上的点,则它与这条线段两个端点的距离相等;逆命题:若一点与这条线段两个端点的距离相等,则此点在线段的垂直平分线上。否命题:若一点不为线段的垂直平分线上的点,则它与这条线段两个端点的距离不相等。逆否命题:若一点与这条线段两个端点的距离不相等,则此点不在线段的垂直平分线上。原命题
若p则q否命题
若┐p则┐q逆否命题
若┐q则┐p逆命题
若q则p互
否互 逆互 逆互
否互 为互 为逆 否逆 否写出下列命题的逆命题,并判断它们的真假:
(1)若X<Y,则Y>X
(2)若a=0,则ab=0(1)逆命题:若Y>X,则X<Y真命题(2)逆命题:若ab=0,则a=0假命题原命题为真,逆命题不一定为真写出下列命题的否命题,并判断它们的真假:
(1)若X<Y,则Y>X
(2)若a=0,则ab=0(1)否命题:若X≥Y,则Y≤X真命题(2)否命题:若a≠0,则ab≠0。假命题原命题为真,否命题不一定为真写出下列命题的逆否命题,并判断它们的真假:
(1)若X<Y,则Y>X
(2)若a=0,则ab= 0(1)逆否命题:若Y≤X,则X≥Y真命题(2)逆否命题:若ab≠0,则a ≠ 0真命题原命题为真,逆否命题为真。
例2: 设原命题是“当 c>0时,若 a > b ,则 a c > b c”,写出它的逆命题、否命题与逆否命题,并分别判断它们的真假:解:逆命题:当 c > 0时, 若 a c > b c , 则 a> b.逆命题为真.否命题:当 c> 0时,若 a ≤ b,则 a c ≤ b c.否命题为真.逆否命题:当 c > 0时,若 a c ≤ b c,则 a ≤ b.逆否命题为真.原命题为真互为逆否关系的两个命题同真假
其余关系的两个命题真假不一定相同原命题:例3:写出下列命题的否定与否命题
(1)正n边形(n≥3)的n个内角全相等
(2)末位数字是0 或5 的整数,能被5整除
(3)零的平方等于0
(4)平行四边形的对角线相等且互相平分解(1)命题的否定:正n边形(n≥3)的n个内角不全相等否命题:不是正n边形(n≥3)的n个内角不全相等(2)命题的否定:末位数字是0 或5 的整数,不能被5整除否命题:末位数字不是0也不是5的整数,不能被5整除(3)命题的否定:零的平方不等于0否命题:不等于零的数的平方不等于0(4)命题的否定:平行四边形的对角线不相等或不互相平分否命题:若四边形不是平行四边形,则它的对角线的对
角线不相等或不互相平分总结:1.写原命题的逆命题,否命题,逆否命题时关键是找出所给原命题的条件p 和结论 q2. 命题p 的否定与否命题
命题p 的否定即非p 只是否定命题 p 的结论
否命题是对原命题“若p 则q ”既否其条件又否其结论写出下列命题的否定及其否命题
(1)菱形的四条边都相等
(2)面积相等的三角形是全等三角形
(3)所有的等边三角形各角都相等
(4)所有的方程都不是不等式
(5)若a bc=0 ,则a, b, c中至少有一个为0
(6)有些质数是奇数
(7)若(x-1) (y+2)=0 ,则x=1或y=-2
(8)若 x2+y2 ≠ 0,则x ≠ 0或y ≠ 0填空:(1)命题”等式两边都乘以同一个数,所得结果仍是等式“的逆命题是___________________________________逆否命题是
____________________________________(2)命题“到圆心的距离不等于半径的直线不是圆的切线”的逆否命题是_____________________________________若一条直线是圆的切线,则它到圆心的距离等于半径。
