人教版选修1-1 常用逻辑用语小结课件(69张)
文档属性
| 名称 | 人教版选修1-1 常用逻辑用语小结课件(69张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览











文档简介
课件69张PPT。常用逻辑用语小结基础知识 自主学习课时作业题型分类 深度剖析内容索引基础知识 自主学习1.简单的逻辑联结词
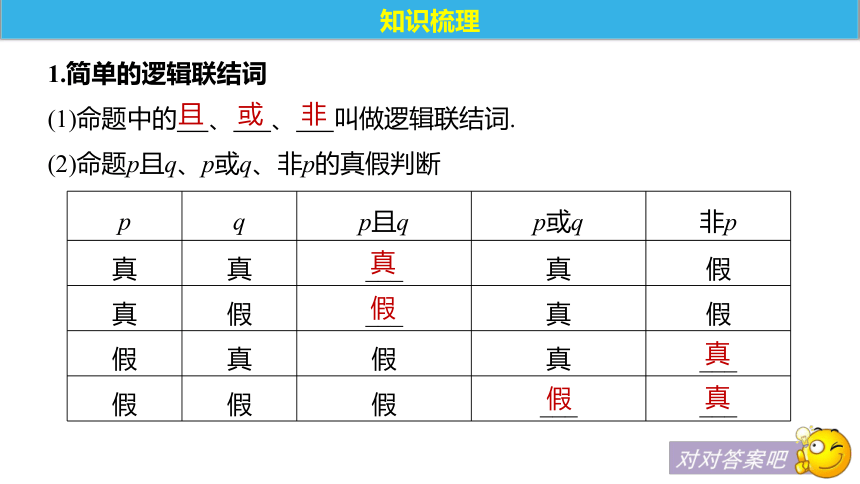
(1)命题中的 、 、 叫做逻辑联结词.
(2)命题p且q、p或q、非p的真假判断知识梳理且非或真假真真假2.全称量词和存在量词
(1)全称量词:短语“所有的”“任意一个”等在逻辑中通常叫做全称量词,用符号“ ”表示.
(2)存在量词:短语“存在一个”“至少有一个”等在逻辑中通常叫做存在量词,用符号“ ”表示.??3.全称命题、特称命题及含一个量词的命题的否定?x∈M,p(x)?x0∈M,綈p(x0)?x0∈M,p(x0)?x∈M,綈p(x)1.含有逻辑联结词的命题真假的判断规律
(1)p∨q:p,q中有一个为真,则p∨q为真,即有真为真.
(2)p∧q:p,q中有一个为假,则p∧q为假,即有假即假.
(3)綈p:与p的真假相反,即一真一假,真假相反.
2.含有一个量词的命题的否定的规律是“改量词,否结论”.
3.命题的否定和否命题的区别:命题“若p,则q”的否定是“若p,则綈q”,否命题是“若綈p,则綈q”.【知识拓展】题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)命题“3≥2”是真命题.( )
(2)命题p和綈p不可能都是真命题.( )
(3)若命题p,q中至少有一个是真命题,则p∨q是真命题.( )
(4)“全等三角形的面积相等”是特称命题.( )
(5)命题綈(p∧q)是假命题,则命题p,q中至少有一个是真命题.( )基础自测√√√××123456题组二 教材改编
2.已知p:2是偶数,q:2是质数,则命题綈p,綈q,p∨q,p∧q中真命题的个数为
A.1 B.2 C.3 D.4123456√解析 p和q显然都是真命题,所以綈p,綈q都是假命题,p∨q,p∧q都是真命题.3.[P28T6(4)]命题“正方形都是矩形”的否定是_____________________
________________.存在一个正方形,这个正方形不是矩形题组三 易错自纠
4.已知命题p,q,“綈p为真”是“p∧q为假”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件解析 由綈p为真知,p为假,可得p∧q为假;反之,若p∧q为假,则可能是p真q假,从而綈p为假,故“綈p为真”是“p∧q为假”的充分不必要条件,故选A.√1234565.下列命题中的假命题是
A.?x0∈R,lg x0=1 B.?x0∈R,sin x0=0
C.?x∈R,x3>0 D.?x∈R,2x>0解析 当x=10时,lg 10=1,则A为真命题;
当x=0时,sin 0=0,则B为真命题;
当x<0时,x3<0,则C为假命题;
由指数函数的性质知,?x∈R ,2x>0,则D为真命题.
故选C.123456√6.已知命题p:?x∈R,x2-a≥0;命题p:?x0∈R,x+2ax0+2-a=0.若命题“p∧q”是真命题,则实数a的取值范围为_____________.123456(-∞,-2]解析 由已知条件可知p和q均为真命题,由命题p为真得a≤0,由命题q为真得Δ=4a2-4(2-a)≥0,即a≤-2或a≥1,所以a≤-2.题型分类 深度剖析1设a,b,c是非零向量.已知命题p:若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中的真命题是
A.p∨q B.p∧q
C.(綈p)∧(綈q) D.p∨(綈q)题型一 含有逻辑联结词的命题的真假判断自主演练√解析 如图所示,若a= ,b= ,c= ,则a·c≠0,命题p为假命题;显然命题q为真命题,所以p∨q为真命题.故选A.2.已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是
A.p∧q B.p∧(綈q) C.(綈p)∧q D.(綈p)∧(綈q)√解析 ∵x>0,∴x+1>1,∴ln(x+1)>ln 1=0.
∴命题p为真命题,∴綈p为假命题.
∵a>b,取a=1,b=-2,而12=1,(-2)2=4,此时a2<b2,
∴命题q为假命题,∴綈q为真命题.
∴p∧q为假命题,p∧(綈q)为真命题,(綈p)∧q为假命题,(綈p)∧(綈q)为假命题.故选B.3.已知命题p:若平面α⊥平面β,平面γ⊥平面β,则有平面α∥平面γ.命题q:在空间中,对于三条不同的直线a,b,c,若a⊥b,b⊥c,则a∥c.对以上两个命题,有以下命题:
①p∧q为真;②p∨q为假;③p∨q为真;④(綈p)∨(綈q)为假.
其中,正确的是________.(填序号)②解析 命题p是假命题,这是因为α与γ也可能相交;
命题q也是假命题,这两条直线也可能异面,相交.“p∨q”“p∧q”“綈p”等形式命题真假的判断步骤
(1)确定命题的构成形式;
(2)判断其中命题p、q的真假;
(3)确定“p∧q”“p∨q”“綈p”等形式命题的真假.命题点1 全称命题、特称命题的真假
典例 下列四个命题:
p1:?x0∈(0,+∞), ;
p2:?x0∈(0,1), ;
p3:?x∈(0,+∞), ;
p4:?x∈, .
其中真命题是
A.p1,p3 B.p1,p4 C.p2,p3 D.p2,p4√题型二 含有一个量词的命题多维探究解析 对于p1,当x0∈(0,+∞)时,总有 成立,故p1是假命题;对于p2,当x0= 时,有1= = > 成立,故p2是真命题;对于p3,结合指数函数y= 与对数函数y= 在(0,+∞)上的图象,可以判断p3是假命题;对于p4,结合指数函数y= 与对数函数y= 在 上的图象,可以判断p4是真命题.命题点2 含一个量词的命题的否定
典例 (1)命题“?x∈R, >0”的否定是
A.?x0∈R, <0 B.?x∈R, ≤0
C.?x∈R, <0 D.?x0∈R, ≤0√解析 全称命题的否定是特称命题,“>”的否定是“≤”.(2)命题“?x0∈R,1<f(x0)≤2”的否定形式是
A.?x∈R,1<f(x)≤2
B.?x0∈R,1<f(x0)≤2
C.?x0∈R,f(x0)≤1或f(x0)>2
D.?x∈R,f(x)≤1或f(x)>2解析 特称命题的否定是全称命题,原命题的否定形式为“?x∈R,f(x)≤1或f(x)>2”.√(1)判定全称命题“?x∈M,p(x)”是真命题,需要对集合M中的每一个元素x,证明p(x)成立;要判断特称命题是真命题,只要在限定集合内找到一个x=x0,使p(x0)成立.
(2)对全(特)称命题进行否定的方法
①找到命题所含的量词,没有量词的要结合命题的含义先加上量词,再改变量词;
②对原命题的结论进行否定.跟踪训练 (1)下列命题是假命题的是
A.?α,β∈R,使cos(α+β)=cos α+cos β
B.?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
C.?x0∈R,使x +ax +bx0+c=0(a,b,c∈R且为常数)
D.?a>0,函数f(x)=ln2x+ln x-a有零点√对于三次函数y=f(x)=x3+ax2+bx+c,当x→-∞时,y→-∞,当x→+∞时,y→+∞,又f(x)在R上为连续函数,故?x0∈R,使x+ax+bx0+c=0,C正确;(2)已知命题p:“?x0∈R, -x0-1≤0”,则綈p为
A.?x0∈R, -x0-1≥0 B.?x0∈R, -x0-1>0
C.?x∈R,ex-x-1>0 D.?x∈R,ex-x-1≥0√解析 根据全称命题与特称命题的否定关系,可得綈p为“?x∈R,ex-x-1>0”,故选C.典例 (1)已知命题p:关于x的方程x2-ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若p∧q是真命题,则实数a的取值范围是________________________.题型三 含参命题中参数的取值范围师生共研解析 若命题p是真命题,则Δ=a2-16≥0,
即a≤-4或a≥4;若命题q是真命题,[-12,-4]∪[4,+∞)∵p∧q是真命题,∴p,q均为真,
∴a的取值范围是[-12,-4]∪[4,+∞).(2)已知f(x)=ln(x2+1),g(x)= -m,若对?x1∈[0,3],?x2∈[1,2],使得
f(x1)≥g(x2),则实数m的取值范围是_____________.解析 当x∈[0,3]时,f(x)min=f(0)=0,当x∈[1,2]时,本例(2)中,若将“?x2∈[1,2]”改为“?x2∈[1,2]”,其他条件不变,
则实数m的取值范围是___________.(1)已知含逻辑联结词的命题的真假,可根据每个命题的真假,利用集合的运算求解参数的取值范围.
(2)对于含量词的命题中求参数的取值范围的问题,可根据命题的含义,利用函数值域(或最值)解决.A.(-∞,-1) B.(-1,3) C.(-3,+∞) D.(-3,1)√则-2<a-1<2,即-1<a<3.(2)已知p:?x∈ R,2x2x+1+m-1存在零点,若“p且q”为真命题,则实数m的取值范围是
________.函数f(x)=4x+2x+1+m-1=(2x+1)2+m-2,故当q为真时,m<1.若f(x)存在零点,常用逻辑用语高频小考点有关四种命题及其真假判断、充分必要条件的判断或求参数的取值范围、量词等问题几乎在每年高考中都会出现,多与函数、数列、立体几何、解析几何等知识相结合,难度中等偏下.解决这类问题应熟练把握各类知识的内在联系.考点分析一、命题的真假判断
典例1 (1)已知a,b都是实数,那么“ ”是“ln a>ln b”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件√所以ln a>ln b不成立,故充分性不成立.(2)已知函数f(x)= 给出下列两个命
题:命题p:?m∈(-∞,0),方程f(x)=0有解,命题q:若m= ,则f(f(-1))=0,则下列命题为真命题的是
A.p∧q B.(綈p)∧q
C.p∧(綈q) D.(綈p)∧(綈q)√解析 因为3x>0,当m<0时,m-x2<0,
所以命题p为假命题;所以命题q为真命题,
逐项检验可知,只有(綈p)∧q为真命题,故选B.二、充要条件的判断
典例2 (1)已知数列{an}的前n项和Sn=Aqn+B(q≠0),则“A=-B”是“数列{an}是等比数列”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件√解析 若A=B=0,则Sn=0,数列{an}不是等比数列;若数列{an}是等比数列,(2)已知圆C:(x-1)2+y2=r2(r>0).设p:0<r<3,q:圆C上至多有2个点到直线x- y+3=0的距离为1,则p是q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件√当r∈(0,1)时,直线与圆相离,圆C上没有到直线的距离为1的点;
当r=1时,直线与圆相离,圆C上只有1个点到直线的距离为1;
当r∈(1,2)时,直线与圆相离,圆C上有2个点到直线的距离为1;
当r=2时,直线与圆相切,圆C上有2个点到直线的距离为1;
当r∈(2,3)时,直线与圆相交,圆C上有2个点到直线的距离为1.
综上,当r∈(0,3)时,圆C上至多有2个点到直线的距离为1,又由圆C上至多有2个点到直线的距离为1,可得0<r<3,故p是q的充要条件,故选C.三、求参数的取值范围
典例3 (1)已知命题p:?x∈[0,1],a≥ex,命题q:?x0∈R, +4x0+a=0,若命题“p∧q”是真命题,则实数a的取值范围是_____.解析 命题“p∧q”是真命题,p和q均是真命题.当p是真命题时,a≥(ex)max=e;当q为真命题时,Δ=16-4a≥0,a≤4,所以a∈[e,4].[e,4](-∞,0]当且仅当x=2时,f(x)min=4,当x∈[2,3]时,g(x)min=22+a=4+a,
依题意知f(x)min≥g(x)min,即4≥a+4,∴a≤0.课时作业1.已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件.则下列命题为真命题的是
A.p∧q B.(綈p)∧(綈q)
C.(綈p)∧q D.p∧(綈q)基础保分练12345678910111213141516√解析 因为指数函数的值域为(0,+∞),所以对任意x∈R,y=2x>0恒成立,故p为真命题;
因为当x>1时,x>2不一定成立,反之,当x>2时,一定有x>1成立,故“x>1”是“x>2”的必要不充分条件,故q为假命题.
则p∧q,綈p为假命题,綈q为真命题,(綈p)∧(綈q),(綈p)∧q为假命题,p∧(綈q)为真命题,故选D.123456789101112131415162.设命题p:函数y=sin 2x的最小正周期为 ;命题q:函数y=cos x的图象关于直线x= 对称,则下列判断正确的是
A.p为真 B.綈q为假
C.p∧q为假 D.p∨q为真解析 函数y=sin 2x的最小正周期为 =π,故命题p为假命题;x= 不是y=cos x的对称轴,故命题q为假命题,故p∧q为假.故选C.√123456789101112131415163.下列命题中为假命题的是
A.?x∈ ,x>sin x
B.?x0∈R,sin x0+cos x0=2
C.?x∈R,3x>0
D.?x0∈R,lg x0=0√12345678910111213141516解析 对于A,令f(x)=x-sin x,则f′(x)=1-cos x,当x∈ 时,f′(x)>0.从而f(x)在 上是增函数,则f(x)>f(0)=0,即x>sin x,故A正确;
对于B,由sin x+cos x= 知,不存在x0∈R,使得sin x0+cos x0=2,故B错误;
对于C,易知3x>0,故C正确;
对于D,由lg 1=0知,D正确.故选B.123456789101112131415164.若定义域为R的函数f(x)不是偶函数,则下列命题中一定为真命题的是
A.?x∈R,f(-x)≠f(x) B.?x∈R,f(-x)=-f(x)
C.?x0∈R,f(-x0)≠f(x0) D.?x0∈R,f(-x0)=-f(x0)√12345678910111213141516解析 由题意知?x∈R,f(-x)=f(x)是假命题,则其否定为真命题,?x0∈R,f(-x0)≠f(x0)是真命题,故选C.5.设命题p:?x0∈(0,+∞),x0+ >3;命题q:?x∈(2,+∞),x2>2x,则下列命题为真的是
A.p∧(綈q) B.(綈p)∧q
C.p∧q D.(綈p)∨q解析 对于命题p,当x0=4时, 故命题p为真命题;对于命题q,当x=4时,24=42=16,即?x0∈(2,+∞),使得 = 成立,故命题q为假命题,所以p∧(綈q)为真命题,故选A.√123456789101112131415166.已知命题p:?x0∈R,cos x0= ;命题q:?x∈R,x2-x+1>0.则下列结论正确的是
A.命题p∧q是真命题
B.命题p∧(綈q)是真命题
C.命题(綈p)∧q是真命题
D.命题(綈p)∨(綈q)是假命题√1234567891011121314151612345678910111213141516所以命题q:?x∈R,x2-x+1>0是真命题.
由此对照各个选项,可知命题(綈p)∧q是真命题.7.下列命题中,真命题是
A.?x0∈R, ≤0
B.?x∈R,2x>x2
C.a+b=0的充要条件是 =-1
D.“a>1,b>1”是“ab>1”的充分条件解析 因为y=ex>0,x∈R恒成立,所以A不正确;
因为当x=-5时,2-5<(-5)2,所以B不正确;
“ =-1”是“a+b=0”的充分不必要条件,C不正确;
当a>1,b>1时,显然ab>1,D正确.√123456789101112131415168.命题p:?x∈R,ax2+ax+1≥0,若綈p是真命题,则实数a的取值范围是
A.(0,4] B.[0,4]
C.(-∞,0]∪[4,+∞) D.(-∞,0)∪(4,+∞)√12345678910111213141516解析 因为命题p:?x∈R,ax2+ax+1≥0,9.命题p的否定是“对所有正数x, >x+1”,则命题p可写为___________________________.解析 因为p是綈p的否定,所以只需将全称命题变为特称命题,再对结论否定即可.1234567891011121314151610.已知函数f(x)的定义域为(a,b),若“?x0∈(a,b),f(x0)+f(-x0)≠0”是假命题,则f(a+b)=______.解析 若“?x0∈(a,b),f(x0)+f(-x0)≠0”是假命题,
则“?x∈(a,b),f(x)+f(-x)=0”是真命题,
即f(-x)=-f(x),则函数f(x)是奇函数,
则a+b=0,即f(a+b)=f(0)=0.12345678910111213141516011.以下四个命题:
①?x∈R,x2-3x+2>0恒成立;②?x0∈Q, =2;③?x0∈R, +1=0;④?x∈R,4x2>2x-1+3x2.其中真命题的个数为___.012345678910111213141516解析 ∵x2-3x+2=0的判别式Δ=(-3)2-4×2>0,
∴当x>2或x<1时,x2-3x+2>0才成立,
∴①为假命题;12345678910111213141516对?x∈R,x2+1≠0,∴③为假命题;
4x2-(2x-1+3x2)=x2-2x+1=(x-1)2≥0,
即当x=1时,4x2=2x-1+3x2成立,∴④为假命题.
∴①②③④均为假命题.故真命题的个数为0.12.已知命题p:?x0∈R,(m+1)·( +1)≤0,命题q:?x∈R,x2+mx+1>0恒成立.若p∧q为假命题,则实数m的取值范围为________________________.解析 由命题p:?x0∈R,(m+1)( +1)≤0,可得m≤-1,由命题q:?x∈R,x2+mx+1>0恒成立,可得-2-1.(-∞,-2]∪(-1,+∞)1234567891011121314151613.已知命题p:x2+2x-3>0;命题q: >1,若“(綈q)∧p”为真,则x的取值范围是____________________________.技能提升练12345678910111213141516(-∞,-3)∪(1,2]∪[3,+∞)所以当q为假命题时,有x≥3或x≤2;
当p为真命题时,由x2+2x-3>0,解得x>1或x<-3,12345678910111213141516解析 因为“(綈q)∧p”为真,即q假p真,得x≥3或1<x≤2或x<-3,
所以x的取值范围是{x|x≥3或1<x≤2或x<-3}.14.下列结论:
①若命题p:?x0∈R,tan x0=1;命题q:?x∈R,x2-x+1>0,则命题“p∧(綈q)”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是
=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题是“若x≠1,则x2-3x+2≠0”.
其中正确结论的序号为________.12345678910111213141516①③解析 ①中命题p为真命题,命题q为真命题,
所以p∧(綈q)为假命题,故①正确;
②当b=a=0时,有l1⊥l2,故②不正确;
③正确,所以正确结论的序号为①③.1234567891011121314151615.已知命题p:?x0∈R, -mx0=0,命题q:?x∈R,x2+mx+1≥0,若p∨(綈q)为假命题,则实数m的取值范围是_____.拓展冲刺练12345678910111213141516[0,2]解析 若p∨(綈q)为假命题,则p假q真.12345678910111213141516所以当x=1时,函数取得极小值f(1)=e,12345678910111213141516由p是假命题,可得0≤m所以当p∨(綈q)为假命题时,m的取值范围是0≤m≤2.16.已知函数f(x)= (x≥2),g(x)=ax(a>1,x≥2).
(1)若?x0∈[2,+∞),使f(x0)=m成立,则实数m的取值范围为_________;12345678910111213141516[3,+∞)当且仅当x=2时等号成立,
所以若?x0∈[2,+∞),使f(x0)=m成立,
则实数m的取值范围为[3,+∞).(2)若?x1∈[2,+∞),?x2∈[2, +∞),使得f(x1)=g(x2),则实数a的取值范围为__________.12345678910111213141516解析 因为当x≥2时,f(x)≥3,g(x)≥a2,
若?x1∈[2,+∞),?x2∈[2,+∞),使得f(x1)=g(x2),本课结束
(1)命题中的 、 、 叫做逻辑联结词.
(2)命题p且q、p或q、非p的真假判断知识梳理且非或真假真真假2.全称量词和存在量词
(1)全称量词:短语“所有的”“任意一个”等在逻辑中通常叫做全称量词,用符号“ ”表示.
(2)存在量词:短语“存在一个”“至少有一个”等在逻辑中通常叫做存在量词,用符号“ ”表示.??3.全称命题、特称命题及含一个量词的命题的否定?x∈M,p(x)?x0∈M,綈p(x0)?x0∈M,p(x0)?x∈M,綈p(x)1.含有逻辑联结词的命题真假的判断规律
(1)p∨q:p,q中有一个为真,则p∨q为真,即有真为真.
(2)p∧q:p,q中有一个为假,则p∧q为假,即有假即假.
(3)綈p:与p的真假相反,即一真一假,真假相反.
2.含有一个量词的命题的否定的规律是“改量词,否结论”.
3.命题的否定和否命题的区别:命题“若p,则q”的否定是“若p,则綈q”,否命题是“若綈p,则綈q”.【知识拓展】题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)命题“3≥2”是真命题.( )
(2)命题p和綈p不可能都是真命题.( )
(3)若命题p,q中至少有一个是真命题,则p∨q是真命题.( )
(4)“全等三角形的面积相等”是特称命题.( )
(5)命题綈(p∧q)是假命题,则命题p,q中至少有一个是真命题.( )基础自测√√√××123456题组二 教材改编
2.已知p:2是偶数,q:2是质数,则命题綈p,綈q,p∨q,p∧q中真命题的个数为
A.1 B.2 C.3 D.4123456√解析 p和q显然都是真命题,所以綈p,綈q都是假命题,p∨q,p∧q都是真命题.3.[P28T6(4)]命题“正方形都是矩形”的否定是_____________________
________________.存在一个正方形,这个正方形不是矩形题组三 易错自纠
4.已知命题p,q,“綈p为真”是“p∧q为假”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件解析 由綈p为真知,p为假,可得p∧q为假;反之,若p∧q为假,则可能是p真q假,从而綈p为假,故“綈p为真”是“p∧q为假”的充分不必要条件,故选A.√1234565.下列命题中的假命题是
A.?x0∈R,lg x0=1 B.?x0∈R,sin x0=0
C.?x∈R,x3>0 D.?x∈R,2x>0解析 当x=10时,lg 10=1,则A为真命题;
当x=0时,sin 0=0,则B为真命题;
当x<0时,x3<0,则C为假命题;
由指数函数的性质知,?x∈R ,2x>0,则D为真命题.
故选C.123456√6.已知命题p:?x∈R,x2-a≥0;命题p:?x0∈R,x+2ax0+2-a=0.若命题“p∧q”是真命题,则实数a的取值范围为_____________.123456(-∞,-2]解析 由已知条件可知p和q均为真命题,由命题p为真得a≤0,由命题q为真得Δ=4a2-4(2-a)≥0,即a≤-2或a≥1,所以a≤-2.题型分类 深度剖析1设a,b,c是非零向量.已知命题p:若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中的真命题是
A.p∨q B.p∧q
C.(綈p)∧(綈q) D.p∨(綈q)题型一 含有逻辑联结词的命题的真假判断自主演练√解析 如图所示,若a= ,b= ,c= ,则a·c≠0,命题p为假命题;显然命题q为真命题,所以p∨q为真命题.故选A.2.已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是
A.p∧q B.p∧(綈q) C.(綈p)∧q D.(綈p)∧(綈q)√解析 ∵x>0,∴x+1>1,∴ln(x+1)>ln 1=0.
∴命题p为真命题,∴綈p为假命题.
∵a>b,取a=1,b=-2,而12=1,(-2)2=4,此时a2<b2,
∴命题q为假命题,∴綈q为真命题.
∴p∧q为假命题,p∧(綈q)为真命题,(綈p)∧q为假命题,(綈p)∧(綈q)为假命题.故选B.3.已知命题p:若平面α⊥平面β,平面γ⊥平面β,则有平面α∥平面γ.命题q:在空间中,对于三条不同的直线a,b,c,若a⊥b,b⊥c,则a∥c.对以上两个命题,有以下命题:
①p∧q为真;②p∨q为假;③p∨q为真;④(綈p)∨(綈q)为假.
其中,正确的是________.(填序号)②解析 命题p是假命题,这是因为α与γ也可能相交;
命题q也是假命题,这两条直线也可能异面,相交.“p∨q”“p∧q”“綈p”等形式命题真假的判断步骤
(1)确定命题的构成形式;
(2)判断其中命题p、q的真假;
(3)确定“p∧q”“p∨q”“綈p”等形式命题的真假.命题点1 全称命题、特称命题的真假
典例 下列四个命题:
p1:?x0∈(0,+∞), ;
p2:?x0∈(0,1), ;
p3:?x∈(0,+∞), ;
p4:?x∈, .
其中真命题是
A.p1,p3 B.p1,p4 C.p2,p3 D.p2,p4√题型二 含有一个量词的命题多维探究解析 对于p1,当x0∈(0,+∞)时,总有 成立,故p1是假命题;对于p2,当x0= 时,有1= = > 成立,故p2是真命题;对于p3,结合指数函数y= 与对数函数y= 在(0,+∞)上的图象,可以判断p3是假命题;对于p4,结合指数函数y= 与对数函数y= 在 上的图象,可以判断p4是真命题.命题点2 含一个量词的命题的否定
典例 (1)命题“?x∈R, >0”的否定是
A.?x0∈R, <0 B.?x∈R, ≤0
C.?x∈R, <0 D.?x0∈R, ≤0√解析 全称命题的否定是特称命题,“>”的否定是“≤”.(2)命题“?x0∈R,1<f(x0)≤2”的否定形式是
A.?x∈R,1<f(x)≤2
B.?x0∈R,1<f(x0)≤2
C.?x0∈R,f(x0)≤1或f(x0)>2
D.?x∈R,f(x)≤1或f(x)>2解析 特称命题的否定是全称命题,原命题的否定形式为“?x∈R,f(x)≤1或f(x)>2”.√(1)判定全称命题“?x∈M,p(x)”是真命题,需要对集合M中的每一个元素x,证明p(x)成立;要判断特称命题是真命题,只要在限定集合内找到一个x=x0,使p(x0)成立.
(2)对全(特)称命题进行否定的方法
①找到命题所含的量词,没有量词的要结合命题的含义先加上量词,再改变量词;
②对原命题的结论进行否定.跟踪训练 (1)下列命题是假命题的是
A.?α,β∈R,使cos(α+β)=cos α+cos β
B.?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
C.?x0∈R,使x +ax +bx0+c=0(a,b,c∈R且为常数)
D.?a>0,函数f(x)=ln2x+ln x-a有零点√对于三次函数y=f(x)=x3+ax2+bx+c,当x→-∞时,y→-∞,当x→+∞时,y→+∞,又f(x)在R上为连续函数,故?x0∈R,使x+ax+bx0+c=0,C正确;(2)已知命题p:“?x0∈R, -x0-1≤0”,则綈p为
A.?x0∈R, -x0-1≥0 B.?x0∈R, -x0-1>0
C.?x∈R,ex-x-1>0 D.?x∈R,ex-x-1≥0√解析 根据全称命题与特称命题的否定关系,可得綈p为“?x∈R,ex-x-1>0”,故选C.典例 (1)已知命题p:关于x的方程x2-ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若p∧q是真命题,则实数a的取值范围是________________________.题型三 含参命题中参数的取值范围师生共研解析 若命题p是真命题,则Δ=a2-16≥0,
即a≤-4或a≥4;若命题q是真命题,[-12,-4]∪[4,+∞)∵p∧q是真命题,∴p,q均为真,
∴a的取值范围是[-12,-4]∪[4,+∞).(2)已知f(x)=ln(x2+1),g(x)= -m,若对?x1∈[0,3],?x2∈[1,2],使得
f(x1)≥g(x2),则实数m的取值范围是_____________.解析 当x∈[0,3]时,f(x)min=f(0)=0,当x∈[1,2]时,本例(2)中,若将“?x2∈[1,2]”改为“?x2∈[1,2]”,其他条件不变,
则实数m的取值范围是___________.(1)已知含逻辑联结词的命题的真假,可根据每个命题的真假,利用集合的运算求解参数的取值范围.
(2)对于含量词的命题中求参数的取值范围的问题,可根据命题的含义,利用函数值域(或最值)解决.A.(-∞,-1) B.(-1,3) C.(-3,+∞) D.(-3,1)√则-2<a-1<2,即-1<a<3.(2)已知p:?x∈ R,2x
________.函数f(x)=4x+2x+1+m-1=(2x+1)2+m-2,故当q为真时,m<1.若f(x)存在零点,常用逻辑用语高频小考点有关四种命题及其真假判断、充分必要条件的判断或求参数的取值范围、量词等问题几乎在每年高考中都会出现,多与函数、数列、立体几何、解析几何等知识相结合,难度中等偏下.解决这类问题应熟练把握各类知识的内在联系.考点分析一、命题的真假判断
典例1 (1)已知a,b都是实数,那么“ ”是“ln a>ln b”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件√所以ln a>ln b不成立,故充分性不成立.(2)已知函数f(x)= 给出下列两个命
题:命题p:?m∈(-∞,0),方程f(x)=0有解,命题q:若m= ,则f(f(-1))=0,则下列命题为真命题的是
A.p∧q B.(綈p)∧q
C.p∧(綈q) D.(綈p)∧(綈q)√解析 因为3x>0,当m<0时,m-x2<0,
所以命题p为假命题;所以命题q为真命题,
逐项检验可知,只有(綈p)∧q为真命题,故选B.二、充要条件的判断
典例2 (1)已知数列{an}的前n项和Sn=Aqn+B(q≠0),则“A=-B”是“数列{an}是等比数列”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件√解析 若A=B=0,则Sn=0,数列{an}不是等比数列;若数列{an}是等比数列,(2)已知圆C:(x-1)2+y2=r2(r>0).设p:0<r<3,q:圆C上至多有2个点到直线x- y+3=0的距离为1,则p是q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件√当r∈(0,1)时,直线与圆相离,圆C上没有到直线的距离为1的点;
当r=1时,直线与圆相离,圆C上只有1个点到直线的距离为1;
当r∈(1,2)时,直线与圆相离,圆C上有2个点到直线的距离为1;
当r=2时,直线与圆相切,圆C上有2个点到直线的距离为1;
当r∈(2,3)时,直线与圆相交,圆C上有2个点到直线的距离为1.
综上,当r∈(0,3)时,圆C上至多有2个点到直线的距离为1,又由圆C上至多有2个点到直线的距离为1,可得0<r<3,故p是q的充要条件,故选C.三、求参数的取值范围
典例3 (1)已知命题p:?x∈[0,1],a≥ex,命题q:?x0∈R, +4x0+a=0,若命题“p∧q”是真命题,则实数a的取值范围是_____.解析 命题“p∧q”是真命题,p和q均是真命题.当p是真命题时,a≥(ex)max=e;当q为真命题时,Δ=16-4a≥0,a≤4,所以a∈[e,4].[e,4](-∞,0]当且仅当x=2时,f(x)min=4,当x∈[2,3]时,g(x)min=22+a=4+a,
依题意知f(x)min≥g(x)min,即4≥a+4,∴a≤0.课时作业1.已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件.则下列命题为真命题的是
A.p∧q B.(綈p)∧(綈q)
C.(綈p)∧q D.p∧(綈q)基础保分练12345678910111213141516√解析 因为指数函数的值域为(0,+∞),所以对任意x∈R,y=2x>0恒成立,故p为真命题;
因为当x>1时,x>2不一定成立,反之,当x>2时,一定有x>1成立,故“x>1”是“x>2”的必要不充分条件,故q为假命题.
则p∧q,綈p为假命题,綈q为真命题,(綈p)∧(綈q),(綈p)∧q为假命题,p∧(綈q)为真命题,故选D.123456789101112131415162.设命题p:函数y=sin 2x的最小正周期为 ;命题q:函数y=cos x的图象关于直线x= 对称,则下列判断正确的是
A.p为真 B.綈q为假
C.p∧q为假 D.p∨q为真解析 函数y=sin 2x的最小正周期为 =π,故命题p为假命题;x= 不是y=cos x的对称轴,故命题q为假命题,故p∧q为假.故选C.√123456789101112131415163.下列命题中为假命题的是
A.?x∈ ,x>sin x
B.?x0∈R,sin x0+cos x0=2
C.?x∈R,3x>0
D.?x0∈R,lg x0=0√12345678910111213141516解析 对于A,令f(x)=x-sin x,则f′(x)=1-cos x,当x∈ 时,f′(x)>0.从而f(x)在 上是增函数,则f(x)>f(0)=0,即x>sin x,故A正确;
对于B,由sin x+cos x= 知,不存在x0∈R,使得sin x0+cos x0=2,故B错误;
对于C,易知3x>0,故C正确;
对于D,由lg 1=0知,D正确.故选B.123456789101112131415164.若定义域为R的函数f(x)不是偶函数,则下列命题中一定为真命题的是
A.?x∈R,f(-x)≠f(x) B.?x∈R,f(-x)=-f(x)
C.?x0∈R,f(-x0)≠f(x0) D.?x0∈R,f(-x0)=-f(x0)√12345678910111213141516解析 由题意知?x∈R,f(-x)=f(x)是假命题,则其否定为真命题,?x0∈R,f(-x0)≠f(x0)是真命题,故选C.5.设命题p:?x0∈(0,+∞),x0+ >3;命题q:?x∈(2,+∞),x2>2x,则下列命题为真的是
A.p∧(綈q) B.(綈p)∧q
C.p∧q D.(綈p)∨q解析 对于命题p,当x0=4时, 故命题p为真命题;对于命题q,当x=4时,24=42=16,即?x0∈(2,+∞),使得 = 成立,故命题q为假命题,所以p∧(綈q)为真命题,故选A.√123456789101112131415166.已知命题p:?x0∈R,cos x0= ;命题q:?x∈R,x2-x+1>0.则下列结论正确的是
A.命题p∧q是真命题
B.命题p∧(綈q)是真命题
C.命题(綈p)∧q是真命题
D.命题(綈p)∨(綈q)是假命题√1234567891011121314151612345678910111213141516所以命题q:?x∈R,x2-x+1>0是真命题.
由此对照各个选项,可知命题(綈p)∧q是真命题.7.下列命题中,真命题是
A.?x0∈R, ≤0
B.?x∈R,2x>x2
C.a+b=0的充要条件是 =-1
D.“a>1,b>1”是“ab>1”的充分条件解析 因为y=ex>0,x∈R恒成立,所以A不正确;
因为当x=-5时,2-5<(-5)2,所以B不正确;
“ =-1”是“a+b=0”的充分不必要条件,C不正确;
当a>1,b>1时,显然ab>1,D正确.√123456789101112131415168.命题p:?x∈R,ax2+ax+1≥0,若綈p是真命题,则实数a的取值范围是
A.(0,4] B.[0,4]
C.(-∞,0]∪[4,+∞) D.(-∞,0)∪(4,+∞)√12345678910111213141516解析 因为命题p:?x∈R,ax2+ax+1≥0,9.命题p的否定是“对所有正数x, >x+1”,则命题p可写为___________________________.解析 因为p是綈p的否定,所以只需将全称命题变为特称命题,再对结论否定即可.1234567891011121314151610.已知函数f(x)的定义域为(a,b),若“?x0∈(a,b),f(x0)+f(-x0)≠0”是假命题,则f(a+b)=______.解析 若“?x0∈(a,b),f(x0)+f(-x0)≠0”是假命题,
则“?x∈(a,b),f(x)+f(-x)=0”是真命题,
即f(-x)=-f(x),则函数f(x)是奇函数,
则a+b=0,即f(a+b)=f(0)=0.12345678910111213141516011.以下四个命题:
①?x∈R,x2-3x+2>0恒成立;②?x0∈Q, =2;③?x0∈R, +1=0;④?x∈R,4x2>2x-1+3x2.其中真命题的个数为___.012345678910111213141516解析 ∵x2-3x+2=0的判别式Δ=(-3)2-4×2>0,
∴当x>2或x<1时,x2-3x+2>0才成立,
∴①为假命题;12345678910111213141516对?x∈R,x2+1≠0,∴③为假命题;
4x2-(2x-1+3x2)=x2-2x+1=(x-1)2≥0,
即当x=1时,4x2=2x-1+3x2成立,∴④为假命题.
∴①②③④均为假命题.故真命题的个数为0.12.已知命题p:?x0∈R,(m+1)·( +1)≤0,命题q:?x∈R,x2+mx+1>0恒成立.若p∧q为假命题,则实数m的取值范围为________________________.解析 由命题p:?x0∈R,(m+1)( +1)≤0,可得m≤-1,由命题q:?x∈R,x2+mx+1>0恒成立,可得-2
当p为真命题时,由x2+2x-3>0,解得x>1或x<-3,12345678910111213141516解析 因为“(綈q)∧p”为真,即q假p真,得x≥3或1<x≤2或x<-3,
所以x的取值范围是{x|x≥3或1<x≤2或x<-3}.14.下列结论:
①若命题p:?x0∈R,tan x0=1;命题q:?x∈R,x2-x+1>0,则命题“p∧(綈q)”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是
=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题是“若x≠1,则x2-3x+2≠0”.
其中正确结论的序号为________.12345678910111213141516①③解析 ①中命题p为真命题,命题q为真命题,
所以p∧(綈q)为假命题,故①正确;
②当b=a=0时,有l1⊥l2,故②不正确;
③正确,所以正确结论的序号为①③.1234567891011121314151615.已知命题p:?x0∈R, -mx0=0,命题q:?x∈R,x2+mx+1≥0,若p∨(綈q)为假命题,则实数m的取值范围是_____.拓展冲刺练12345678910111213141516[0,2]解析 若p∨(綈q)为假命题,则p假q真.12345678910111213141516所以当x=1时,函数取得极小值f(1)=e,12345678910111213141516由p是假命题,可得0≤m
(1)若?x0∈[2,+∞),使f(x0)=m成立,则实数m的取值范围为_________;12345678910111213141516[3,+∞)当且仅当x=2时等号成立,
所以若?x0∈[2,+∞),使f(x0)=m成立,
则实数m的取值范围为[3,+∞).(2)若?x1∈[2,+∞),?x2∈[2, +∞),使得f(x1)=g(x2),则实数a的取值范围为__________.12345678910111213141516解析 因为当x≥2时,f(x)≥3,g(x)≥a2,
若?x1∈[2,+∞),?x2∈[2,+∞),使得f(x1)=g(x2),本课结束
