人教版选修1-1 常用逻辑用语复习课件(21张)
文档属性
| 名称 | 人教版选修1-1 常用逻辑用语复习课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 544.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览






文档简介
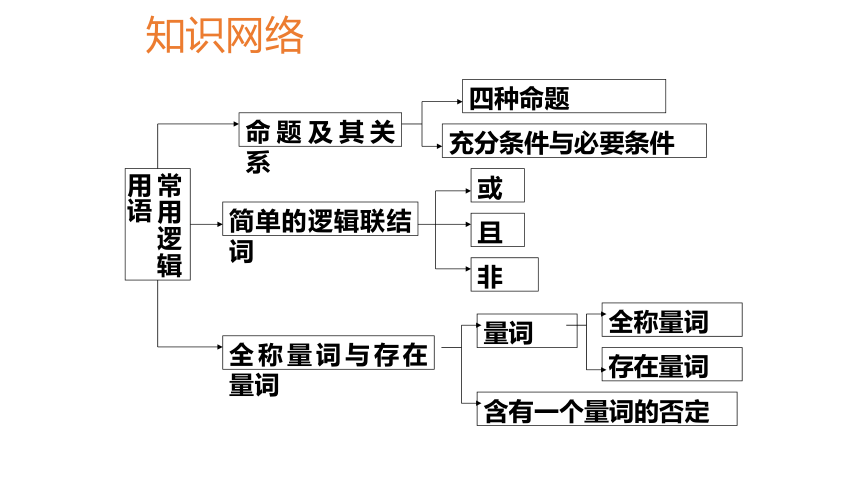
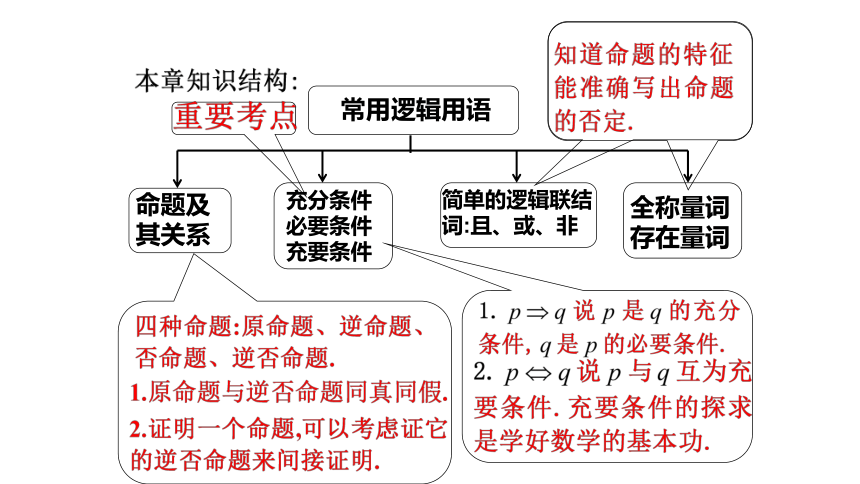
课件21张PPT。常用逻辑用语复习知识网络 全称量词存在量词含有一个量词的否定命题及其关系全称量词存在量词充分条件必要条件充要条件简单的逻辑联结词:且、或、非1.四种命题及其相互关系,特别是互为逆否命题的两个命题同真假.
2.充分条件、必要条件、充要条件的判断,会用充要条件的知识解决一些与其它知识相关的问题.
3.正确使用逻辑联结词“或” “且” “非”,会判断复合命题的真假.
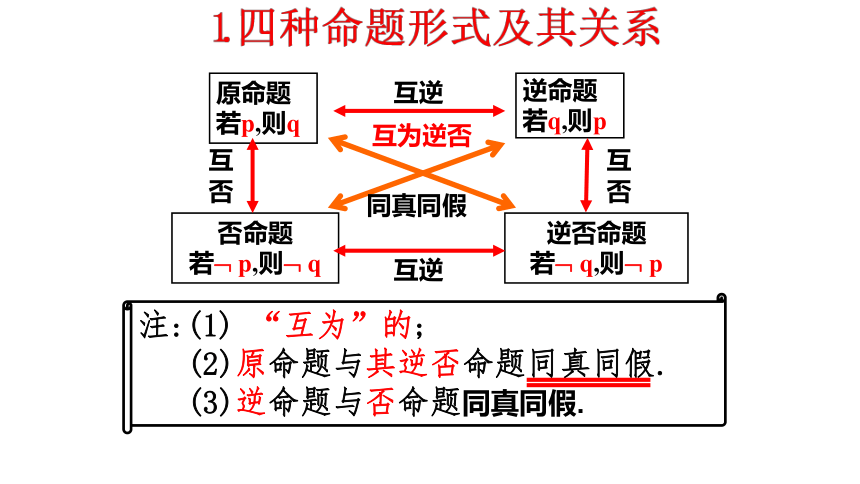
4.会判断全称命题与特称命题,会写命题的否定.注:(1) “互为”的;
(2)原命题与其逆否命题同真同假.
(3)逆命题与否命题同真同假.原命题
若p,则q逆否命题
若? q,则? p否命题
若? p,则? q逆命题
若q,则p互逆互 否互 否互逆互为逆否同真同假(1)从概念的角度去理解.
①若p?q,则称p是q的充分条件,q是p的必要条件.
②若p?q,则p是q的充要条件.
⑧若p? q,且q ? p,则称p是q的充分不必要条件.
④若p? q,且q? p,则称p是q的必要不充分条件.
⑤若p? q,且q? p,则称p是q的既不充分也不必要条件对于充分条件和必要条件,要能够正确地理解和判断(2)从命题的角度去理解.
设原命题为“若p,则q”,则
①若原命题为真,则p是q的 .
②若逆命题为真,则p是q的 .
③若原命题和逆命题都为真,则p是q的 .
④若原命题为真而逆命题为假,则p是q的 .
⑤若原命题为假而逆命题为真,则p是q的 .
⑥若原命题和逆命题都为假,则p是q的 .充分条件必要条件充要条件充分不必要条件必要不充分件既不充分也不必要条件 (1).三种形式的命题分别为“p且q”“p或q”“非p”,记作“p? q”“p?q"“?p”.
判断这三种形式命题的基本依据是命题中是否含有(或隐含)逻辑联结的词“或”“且”“非”.(2).三种形式命题的真假
“p或q” ─ 只要p、q中有一个为真就为真.(p、q同时为假才为假.)
“p且q”─ p、q同时为真才为真.
“? p”─ p的全盘否定,p与?p一真一假.基础演练1.分别写出下列的逆命题、否命题、逆否命题,并判断它们的真假.
(1)若ab=0,则a=0或b=0;
(2)若x2+y2=0,则x、y全为零.2.在下列四个结论中,正确的是( )
(1)x2>4是x3<-8的必要不充分条件;
(2)在△ABC中, “AB2+AC2=BC2”是“ △ABC为直角三角形 ”的充要条件;
(3)若a、b∈R,则“a2+b2≠0”是“a 、b全不为0”的充要条件;
(4)若a、b∈R,则“a2+b2≠0”是“a 、b不全为0”的充要条件.
A.(1)(2) B.(3)(4) C.(1)(4) D.(2)(3)C3.指出下列命题的真假:
(1)不等式x2+2≤0没有实数解;
(2)-1是偶数或奇数.(1)真命题(2)真命题4.判断下列命题是全称命题还是特称命题,并判断其真假.
(1)对数函数都是单调函数;
(2)至少有一个整数,它既能被2整除,又能被5整除.(1)全称命题,真命题
(2)特称命题,真命题典型例题 题型1 四种命题例1 有下列四个命题:
①“若x+y=0,则x,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④“不等边三角形的三个内角相等”的逆命题.
其中真命题的序号为________.①③题型2 充要条件问题例2.已知关于x的方程 (1?a)x2+(a+2)x?4=0 a?R 求:1) 方程有两个正根的充要条件; 2) 方程至少有一个正根的充要条件。1)10,且?P是?q的必要不充分条件,求a的取值范围.解:由?P是?q的必要不充分条件,转化成它的逆否命题q是P的必要不充分条件,即P是q的充分不必要条件
也就是p?q且q ? p.
化简条件p得,A={x|3a化简条件q得,B={x|x<-4或x≥-2}分析:本题可依据四种命题间的关系进行等价转化.题型3 全称命题、特称命题及其否定例4 已知命题p:存在x∈R,x2+2x-m=0;命题q:对任意的x∈R,mx2+mx+1>0.
①若命题p为真命题,求实数m的取值范围;
②若命题q为假命题,求实数m的取值范围;
③若命题p或q为真命题,且p且q为假命题,求实数m的取值范围.解:①若命题p为真命题,则x2+2x-m=0有实根,所以Δ=4+4m≥0,所以m≥-1,即m的取值范围为[-1,+∞).
②若命题q为假命题,则
a.m=0时,不合题意;
b.m>0时,Δ=m2-4m≥0,得m≥4;
c.m<0时,符合题意.
综上:实数m的取值范围为(-∞,0)∪[4,+∞).③由①得p为真命题时,m≥-1;p为假命题时,m<-1,由②得q为真命题时,0≤m<4;q为假命题时,m<0或m≥4,
因为“p或q”为真命题,且“p且q”为假命题,所以“p真,且q假”或“p假,且q真”,
所以m<0或m≥4,(m≥-1,)或0≤m<4,(m<-1,)
解得实数m的取值范围为[-1,0)∪[4,+∞).题型4 逻辑联结词的问题例3.给定两个命题,P:对任意实数x 都有 恒成立;Q:关于x的方程 有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
2.充分条件、必要条件、充要条件的判断,会用充要条件的知识解决一些与其它知识相关的问题.
3.正确使用逻辑联结词“或” “且” “非”,会判断复合命题的真假.
4.会判断全称命题与特称命题,会写命题的否定.注:(1) “互为”的;
(2)原命题与其逆否命题同真同假.
(3)逆命题与否命题同真同假.原命题
若p,则q逆否命题
若? q,则? p否命题
若? p,则? q逆命题
若q,则p互逆互 否互 否互逆互为逆否同真同假(1)从概念的角度去理解.
①若p?q,则称p是q的充分条件,q是p的必要条件.
②若p?q,则p是q的充要条件.
⑧若p? q,且q ? p,则称p是q的充分不必要条件.
④若p? q,且q? p,则称p是q的必要不充分条件.
⑤若p? q,且q? p,则称p是q的既不充分也不必要条件对于充分条件和必要条件,要能够正确地理解和判断(2)从命题的角度去理解.
设原命题为“若p,则q”,则
①若原命题为真,则p是q的 .
②若逆命题为真,则p是q的 .
③若原命题和逆命题都为真,则p是q的 .
④若原命题为真而逆命题为假,则p是q的 .
⑤若原命题为假而逆命题为真,则p是q的 .
⑥若原命题和逆命题都为假,则p是q的 .充分条件必要条件充要条件充分不必要条件必要不充分件既不充分也不必要条件 (1).三种形式的命题分别为“p且q”“p或q”“非p”,记作“p? q”“p?q"“?p”.
判断这三种形式命题的基本依据是命题中是否含有(或隐含)逻辑联结的词“或”“且”“非”.(2).三种形式命题的真假
“p或q” ─ 只要p、q中有一个为真就为真.(p、q同时为假才为假.)
“p且q”─ p、q同时为真才为真.
“? p”─ p的全盘否定,p与?p一真一假.基础演练1.分别写出下列的逆命题、否命题、逆否命题,并判断它们的真假.
(1)若ab=0,则a=0或b=0;
(2)若x2+y2=0,则x、y全为零.2.在下列四个结论中,正确的是( )
(1)x2>4是x3<-8的必要不充分条件;
(2)在△ABC中, “AB2+AC2=BC2”是“ △ABC为直角三角形 ”的充要条件;
(3)若a、b∈R,则“a2+b2≠0”是“a 、b全不为0”的充要条件;
(4)若a、b∈R,则“a2+b2≠0”是“a 、b不全为0”的充要条件.
A.(1)(2) B.(3)(4) C.(1)(4) D.(2)(3)C3.指出下列命题的真假:
(1)不等式x2+2≤0没有实数解;
(2)-1是偶数或奇数.(1)真命题(2)真命题4.判断下列命题是全称命题还是特称命题,并判断其真假.
(1)对数函数都是单调函数;
(2)至少有一个整数,它既能被2整除,又能被5整除.(1)全称命题,真命题
(2)特称命题,真命题典型例题 题型1 四种命题例1 有下列四个命题:
①“若x+y=0,则x,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④“不等边三角形的三个内角相等”的逆命题.
其中真命题的序号为________.①③题型2 充要条件问题例2.已知关于x的方程 (1?a)x2+(a+2)x?4=0 a?R 求:1) 方程有两个正根的充要条件; 2) 方程至少有一个正根的充要条件。1)1
也就是p?q且q ? p.
化简条件p得,A={x|3a
①若命题p为真命题,求实数m的取值范围;
②若命题q为假命题,求实数m的取值范围;
③若命题p或q为真命题,且p且q为假命题,求实数m的取值范围.解:①若命题p为真命题,则x2+2x-m=0有实根,所以Δ=4+4m≥0,所以m≥-1,即m的取值范围为[-1,+∞).
②若命题q为假命题,则
a.m=0时,不合题意;
b.m>0时,Δ=m2-4m≥0,得m≥4;
c.m<0时,符合题意.
综上:实数m的取值范围为(-∞,0)∪[4,+∞).③由①得p为真命题时,m≥-1;p为假命题时,m<-1,由②得q为真命题时,0≤m<4;q为假命题时,m<0或m≥4,
因为“p或q”为真命题,且“p且q”为假命题,所以“p真,且q假”或“p假,且q真”,
所以m<0或m≥4,(m≥-1,)或0≤m<4,(m<-1,)
解得实数m的取值范围为[-1,0)∪[4,+∞).题型4 逻辑联结词的问题例3.给定两个命题,P:对任意实数x 都有 恒成立;Q:关于x的方程 有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
