北师大版八年级上册数学一次函数专题复习教案(共五个专题,附答案)
文档属性
| 名称 | 北师大版八年级上册数学一次函数专题复习教案(共五个专题,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 00:00:00 | ||
图片预览




文档简介
前 言
经过对成都近4年各大学校八年级上半年考试试卷的分析发现,无论是四七九中,还是嘉祥、成外、实外、西川、师大一中等学校,一次函数在八年级上无疑成为了各大学校的考试焦点,而且函数也是初二两级分化的导火线,因此学好一次函数迫在眉睫。为了面对接下来的一场硬仗,首先应对成都市各大学校八上一次函数考题作必要分析。
一、整体特点
1.主要考查重难点基础知识,几乎无偏题怪题;
2.试卷结构、题型保持平稳,但在不断寻求变化,推陈出新;
3.B卷一次函数解答题大多以8+12为主(8分应用题+12分一次函数与几何综合).
二、各大学校八上的一次函数考查统计(注:这是近4年各学校考查的平均值)
学校 A卷选填 A卷解答 B卷填空 B卷解答 考试占比
石室联中 18 8 8 8+12 36.0%
七中育才 18 8 8 10+12 37.3%
树德实验 15 14 8 8+12 38.0%
嘉祥 24 18 8 8+12 46.7%
成外 15 6 8 8+12 32.7%
实外 12 10 8 8+12 33.3%
西川 18 14 8 8+12 40.0%
师大一中 27 14 8 8+12 46.0%
三、考点分析
1.选择、填空题及A卷解答题以基础知识考查为主:
(1)平面直角坐标系基础知识;
(2)一次函数定义、图像、性质、解析式;
(3)一次函数的图像变换及代数综合.
2.B卷解答题考查比较综合:
(1)应用题(比较基础,但需多加练习);
(2)一次函数与几何综合:面积、折叠、全等、动态问题、等腰三角形存在问题.(最后两个知识点在初二的讲义会讲到)
为了改善一次函数的吸收消化情况,提高知识熟练度及知识的灵活运用能力,所以针对一次函数的考点编写配套练习辅助一次函数的学习。配套练习一共分为两大板块:复习巩固(必做)和能力拓展(根据情况选做)。复习巩固以课上知识的重难点、易错点进行复习,能力拓展主要提高知识的灵活运用能力。“冰冻三尺,非一日之寒;为山九仞,岂一日之功。希望同学们通过平时的积累在考试中脱颖而出,金榜题名!
目 录
专题一 平面直角坐标系 1
专题二 函数初步及一次函数 3
专题三 一次函数和代数综合 5
专题四 一次函数和几何综合(一) 7
专题五 一次函数和几何综合(二) 11
初一直升班配套练习(答案) 14
专题一 平面直角坐标系
【本讲知识点回顾】
点A在第三象限内,A到x轴的距离与到y轴的距离之比为,到原点的距离为则点A的坐标_______.
在平面直角坐标系中,若点、都位于坐标轴的角平分线上,那么_______.
已知线段,MN∥x轴,若点M坐标为,且点N在第二象限,则N点关于x轴对称的点的坐标为_______.
将点A向上平移3个单位,再向右平移5个单位得到点,已知点A不在任何象限,则线段的中点坐标是_______.
将点向上平移3个单位,再关于y轴对称,得到的点位于第二象限,则符合条件的a的所有整数和的平方根是_______.
在平面直角坐标系中,已知点关于原点的对称点在第二象限内,且m为整数;点在x轴上,求点A到点B的距离?
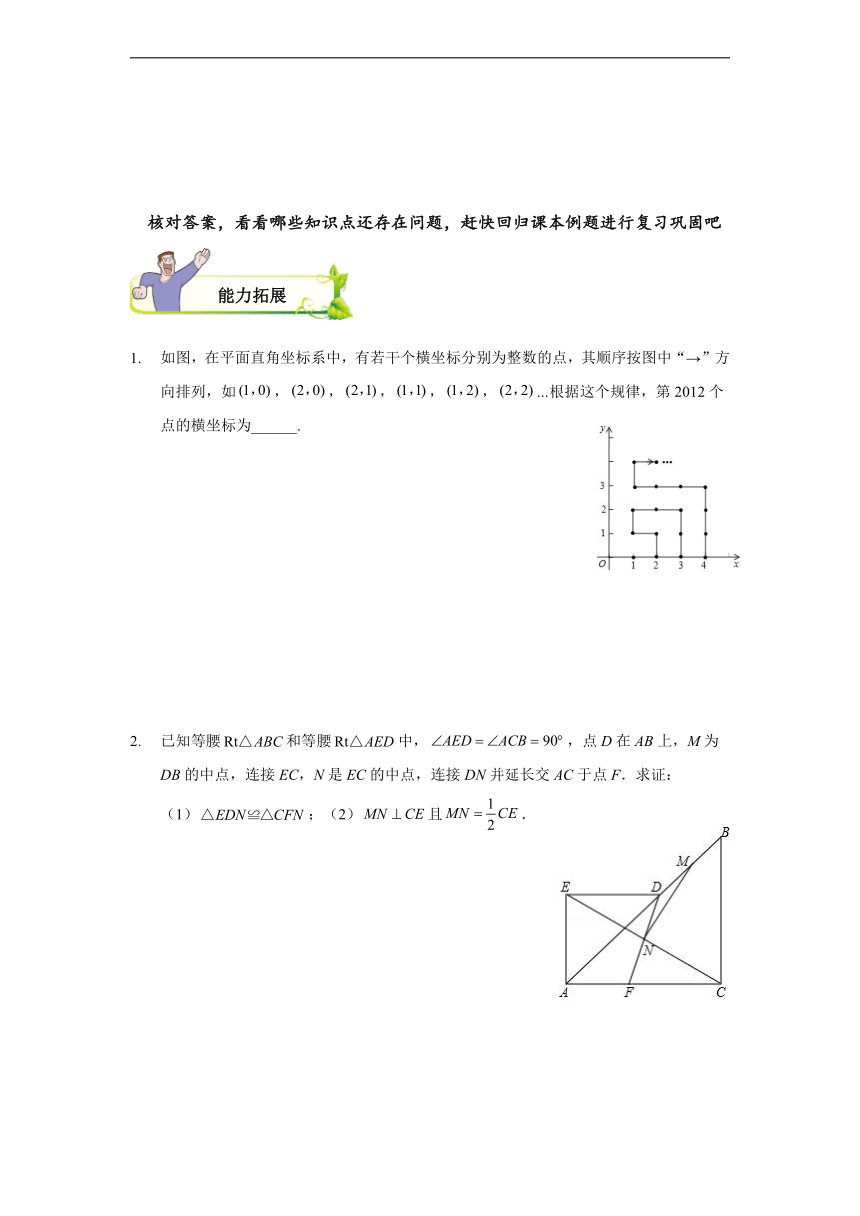
核对答案,看看哪些知识点还存在问题,赶快回归课本例题进行复习巩固吧
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如,,,,,…根据这个规律,第2012个点的横坐标为______.
已知等腰和等腰中,,点D在AB上,M为DB的中点,连接EC,N是EC的中点,连接DN并延长交AC于点F.求证:
(1);(2)且.
专题二 函数初步及一次函数
【本讲知识点回顾】
若函数是关于x的正比例函数,则m的值为__________,n的值为__________.若是关于x的一次函数,那么m的值为__________.
和在同一坐标系中的图象大致是( )
A. B. C. D.
一次函数;当m_________时,图象经过原点;当m________时,y随x增大而增大;当m 时,图象不经过第一象限.
点在直线上,且,则点P到原点的距离为__________.
已知一次函数的图象经过点,,,则c的值为__________.
一次函数,当时,函数值范围为,求一次函数的解析式.
核对答案,看看哪些知识点还存在问题,赶快回归课本例题进行复习巩固吧
已知一次函数(m,n为实数)的图像经过第一、三、四象限,化简:__________.
一次函数图象经过、,则的值为_______.
设,关于x的一次函数,当1≤ x ≤2时= .
某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:设每天生产A种品牌白酒x瓶,每天获利y元.
(1)请写出y关于x的函数关系式;
(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?
A B
成本(元/瓶) 50 35
利润(元/瓶) 20 15
专题三 一次函数和代数综合
【本讲知识点回顾】
函数的图像向下平移3个单位,接着向左平移2个单位,再关于x轴对称,最终得到的函数解析式为__________.
平面直角坐标系中,若一次函数图象与直线交于点,且与直无交点,则该一次函数解析式为__________;若一次函数图象与直线相交于点,且与直线垂直,则该一次函数的解析式为__________.
如图,平面直角坐标系中直线与的交点的横坐标为,则关于x的不等式的整数解为__________.
求证:一次函数的图象恒过一定点,并求这个定点.
一次函数与图象在第四象限内交于一点,求整数的值.
核对答案,看看哪些知识点还存在问题,赶快回归课本例题进行复习巩固吧
若方程组有无穷多组解,则的值为 .
一个一次函数图象与直线平行,与x轴、y轴的交点分别为A、B,并且过点,则在线段AB上(包括端点A、B),横、纵坐标都是整数的点有 个.
小明到服装店进行社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元,乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500元,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
专题四 一次函数和几何综合(一)
【本讲知识点回顾】
设直线(n为自然数)的图像与两坐标轴所围成的三角形的面积为,则的值为_______.
如图,在平面直角坐标系xOy中,已知正比例函数与一次函数的图象交于点A.
(1)求点A的坐标;
(2)x轴上有一点,过点P作x轴的垂线(垂线位于点A的右侧)分别交和的图象于点B、C,连接OC.若,求OAC的面积.
如图1,已知直线l经过点,,且交x轴于B点;
(1)求直线l的解析式;
(2)过点作直线交于,交x轴于,过作于,若,,求证:;
(3)如图2,为x轴上点左侧任一点,以为直角边作等腰Rt△,其中,直线交y轴于,当P在x轴上运动时,求证:线段OQ长不变.
核对答案,看看哪些知识点还存在问题,赶快回归课本例题进行复习巩固吧
A、B分别是x轴上位于原点左右两侧的点,点在第一象限,直线PA交y轴于点,直线PB交y轴于点D,. 求(1)的面积;(2)求点A坐标及m的值;(3)若,求直线BD的解析式.
专题五 一次函数和几何综合(二)
【本讲知识点回顾】
的顶点坐标分别为,,,O是原点.
(1)求中,边上中线所在直线的解析式;
(2)试在和边上分别找一点D、E,使的周长最短.画出点、两
点的位置图形,简述作图方法.
如图1,在直角坐标系中放入一个矩形纸片ABCO,OC长为9,BC长为15,将纸片翻折后,点B恰好落在x轴上,记为B,折痕为CE,那么折痕CE所在直线的解析式是____________.
如图2,直线与轴、轴分别交于点和点,是轴上的一点,若将△沿直线折叠,点恰好落在轴正半轴上的点处,则直线的解析式为____________.
图1 图2
直线分别与x轴、y轴交于两点.
(1)求两点的坐标.
(2)把以直线为轴翻折,点落在平面上的点处,以为一边作等边,求点的坐标.
核对答案,看看哪些知识点还存在问题,赶快回归课本例题进行复习巩固吧
如图所示,已知直线与x、y轴交于B、C两点,,在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个,第3个,…则第n个等边三角形的边长等于________.
为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:
目的地车型 A村(元/辆) B村(元/辆)
大货车 800 900
小货车 400 600
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
初一直升班配套练习(答案)
专题一 平面直角坐标系
(
复习巩固
)
1、 ; 考查知识点:象限 + 点到特殊直线的距离 + 两点间距离公式.
2、 或; 考查知识点:坐标系中的特殊直线 或 点到特殊直线的距离.
3、 ; 考查知识点:坐标系中的特殊直线 + 象限 + 点的对称.
4、 ; 考查知识点:点的平移 + 坐标轴 + 中点坐标公式.
5、 ; 考查知识点:点的平移 + 点的对称 + 象限.
6、 ; 考查知识点:点的对称 + 象限 + 坐标轴 + 两点间距离公式.
(
能力拓展
)
1、 解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的
横坐标的平方,例如:
右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,…
右下角的点的横坐标为n时,共有n2个,
∵452=2025,45是奇数,
∴第2025个点(45,0);第2012个点(45,13);故第2012个点的横坐标为45.
规律: 以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以该数为横坐标,纵坐标为0结束,当右下角的点横坐标是偶数时,以1为横坐标,纵坐标为右下角横坐标的偶数减1的点结束.
2、 证明:(1)∵△ABC和△AED是等腰直角三角形,∠AED=∠ACB=90°,
∴∠EAD=∠EDA=∠BAC=∠ABC=45°,
∴∠EAC=90°,
∴ED∥FC,
∴∠EDN=∠CFN,
∵N是EC的中点,
∴EN=CN,
在△EDN和△CFN中,
∴△EDN△CFN(AAS);
(2)(法一)连接EM并延长到H,使EM=MH,连接CH、CM、BH,
在△EDM和△FBM中,,
∴△EDM≌△HBM(SAS),
∴BH=DE=AE,∠HBM=∠EDM=135°,
∴∠HBC=∠EAC=90°,
在和中,,
∴△EAC≌△HBC(SAS),
∴HC=CE,且HC⊥CE
∵点M、N分别是EH、EC的中点,
∴,且MN // HC
∴MN⊥CE,且.
(2)(法二)【思路】:连接BF,则MN为△BDF的中位线,只需要证明
△EAC≌△FCB,即可得到MN⊥CE,且.(此种方法稍微简单一些) 18
专题二 函数初步及一次函数
(
复习巩固
)
1、 ,,7; 考查知识点:正比例函数定义 + 一次函数定义.
2、 C; 考查知识点:一次函数的图像.
3、 ,,; 考查知识点:一次函数的图像 + 性质.
4、 ; 考查知识点:一次函数解析式.
5、 ; 考查知识点:一次函数的图像 + 解析式.
6、 或; 考查知识点:一次函数的图像 + 性质 + 解析式.
(
能力拓展
)
1、 ; 【解析】由题意得 即,所以化简得:原式= -1.
2、 9; 【解析】由题意得,,故
3、 ; 【解析】,∵,∴当x =1时,
4、 解:(1)A种品牌白酒x瓶,则B种品牌白酒(600﹣x)瓶,
依题意得:y=20x+15(600﹣x)=5x+9000;
(2)A种品牌白酒x瓶,则B种品牌白酒(600﹣x)瓶,
依题意得:50x+35(600﹣x)≥ 26400,解得x ≥ 360,
∴每天至少获利y=5x+9000=10800.
专题三 一次函数和代数综合
(
复习巩固
)
1、 ; 考查知识点:一次函数的图像变换(平移,对称).
2、 ,; 考查知识点:一次函数和方程综合 + 特殊位置关系.
3、 ; 考查知识点:一次函数和不等式综合.
【解析】与x轴的交点为(-4,0),结合函数图像:由知,
;由,结合图像得;所以.
4、 过定点; 考查知识点:一次函数和方程(组)综合.
【解析】可化为:;当时,,所以原一次函
数图像恒过定点.
5、 ,0,1; 考查知识点:一次函数和方程(组)综合 + 象限.
(
能力拓展
)
1、 5;
【解析】由题意得,所以;则.
2、 4;
【解析】∵直线AB与一次函数的图象与直线平行,
∴设直线的解析式是,
∵图象过点,
∴代入得:,故,
∴直线AB的解析式为,
∵当时,,当时,;
∴A,B;故线段AB上点的横坐标取值范围为:,
∵,
∴当x是整数且5x﹣75是4的整倍数时,点的坐标是整数,
即x=3,7,11,15时,y =﹣15,﹣10,﹣5,0;
故共有4个点,
3、 解:(1)设甲种服装购进x件,则乙种服装购进(100﹣x)件,
根据题意得:,
解得:65≤ x ≤75,
∴甲种服装最多购进75件;
(2)设总利润为W元,
即.
①当0<a<10时,10﹣a>0,W随x增大而增大,
当x=75时,W有最大值,即此时购进甲种服装75件,乙种服装25件;
②当a=10时,所以按哪种方案进货都可以;
③当10<a<20时,10﹣a<0,W随x增大而减小.
当x =65时,W有最大值,即此时购进甲种服装65件,乙种服装35件.
专题四 一次函数和几何综合(一)
(
复习巩固
)
1、 ; 考查知识点:直线与坐标轴围成的面积.
【解析】……
2、 (1)A;(2)14; 考查知识点:割补或铅锤法.
【解析】(2)过点A作x轴的垂线,垂足为D
在中,由勾股定理得,.
∴.
∵P,∴B,C,
∴, ∴,解得a =8,
∴.
(也可以求出AC与x轴的交点,再使用铅锤法)
3、 (1); 考查知识点:一次函数和全等综合.
(2)证明:延长交y轴于点(如图1),根据,证明,
得到,再证明即可.
(3)证明:过点作轴于点(如图2),易证为等腰直角三角形
所以恒成立,得到.
图1 图2
(
能力拓展
)
1、 解:(1);
(2)直线过与得:(点斜式),
令得:,∴,
∴,故
∴,∴;
(3);
由可知为中点,
∴,
∴直线的解析式为.
专题五 一次函数和几何综合(二)
(
复习巩固
)
1、 解:(1)边上中点坐标为,则边上中线所在直线的解析式:.
(2)如图,作出点关于线段、的对称点、,连接两点与、的交点即为所求点、. 考查知识点:一次函数和将军饮马.
2、 ; 考查知识点:一次函数与折叠.
【解析】根据题意可得,
∵
∴
∴
设,则;
由勾股定理可得,则E点坐标为
所以的解析式为.(点斜式或两点式)
3、 ; 考查知识点:一次函数与折叠 + 斜率与倾斜角.
根据题意,得:,
在中,,,
∴,
中,
∴,
设直线的解析式为:
∴,解得
所以直线的解析式为
4、 考查知识点:一次函数与折叠 + 斜率与倾斜角.
(1)如图所示,令,由得;
令,由得.
所以点的坐标为,点的坐标为.
(2)由(1)知,,故.
∵和关于成轴对称,
∴,,从而.
过点作垂直轴于点,
则在中:,,
故,
从而点的坐标为.
连接,因为,,故为等边三角形.
过点作平行于轴,并截取,则.
连接,则为等边三角形.`
作垂直轴于点,则,
所以,,
则点的坐标为,从而点的坐标为或.
(
能力拓展
)
1、 ;
∵,
∴BC=2,∴∠OBC =30°,∠OCB =60°.
∵△AA1B1为等边三角形,∴∠A1 AB1=60°,
∴∠COA1=30°,则∠CA1O=90°.
在中,,
同理得:,
依此类推,第n个等边三角形的边长等于.
2、 解:(1)设大货车用x辆,小货车用y辆,
根据题意得: 解得:.
∴大货车用8辆,小货车用7辆.
(2)
即y =100x+9400.(3≤ x ≤ 8,且x为整数).
(3)由题意得:12x+8(10﹣x)≥100,解得:x ≥5,
∵3≤ x ≤ 8,∴5≤ x ≤ 8且为整数,
∵y =100x+9400中k =100>0,
∴y随x的增大而增大,
∴当x=5时,y最小,
最小值为y =100×5+9400=9900(元).
答:使总运费最少的调配方案是:5辆大货车、5辆小货车前往A村;3辆大货车、2辆小货车前往B村.最少运费为9900元.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
