选修4-1第二讲 直线与圆的位置关系 圆内接四边形的性质与判定定理 课件22张PPT
文档属性
| 名称 | 选修4-1第二讲 直线与圆的位置关系 圆内接四边形的性质与判定定理 课件22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 241.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览



文档简介
课件22张PPT。圆内接四边形的性质
与判定定理一、知识回顾:1、∠α叫做圆O的
2、∠β叫做圆O的
3、∠α与∠β的关系是
4、圆心角的度数等于它所对的 的度数
5、圆周角的度数等于它所对的 的度数
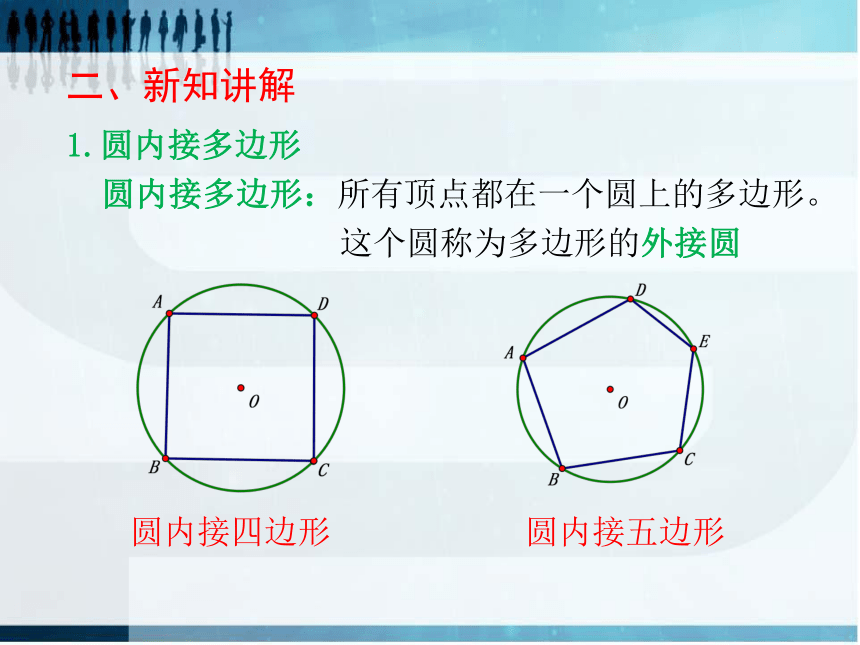
的圆心角弧长一半圆周角弧长二、新知讲解圆内接多边形:所有顶点都在一个圆上的多边形。1.圆内接多边形这个圆称为多边形的外接圆圆内接四边形圆内接五边形
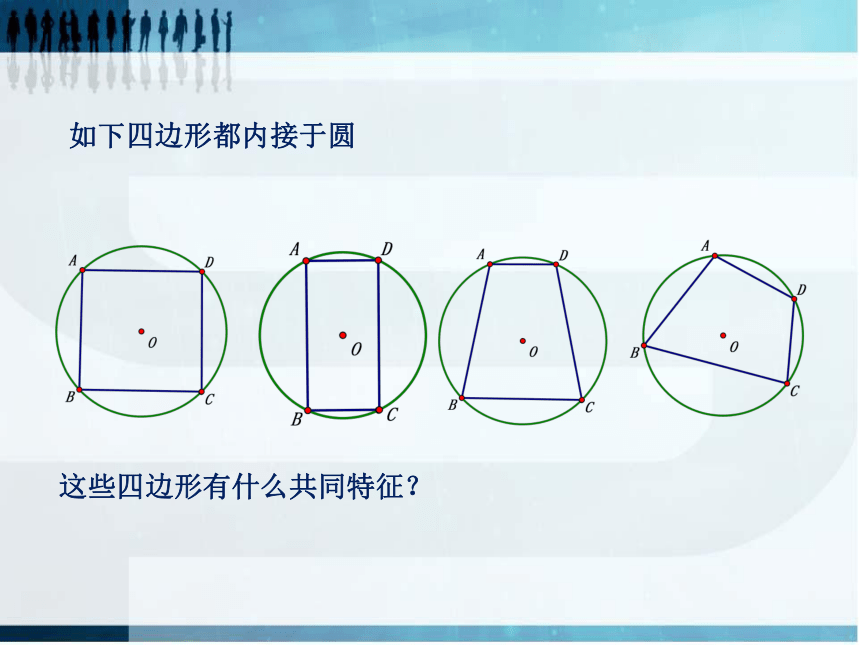
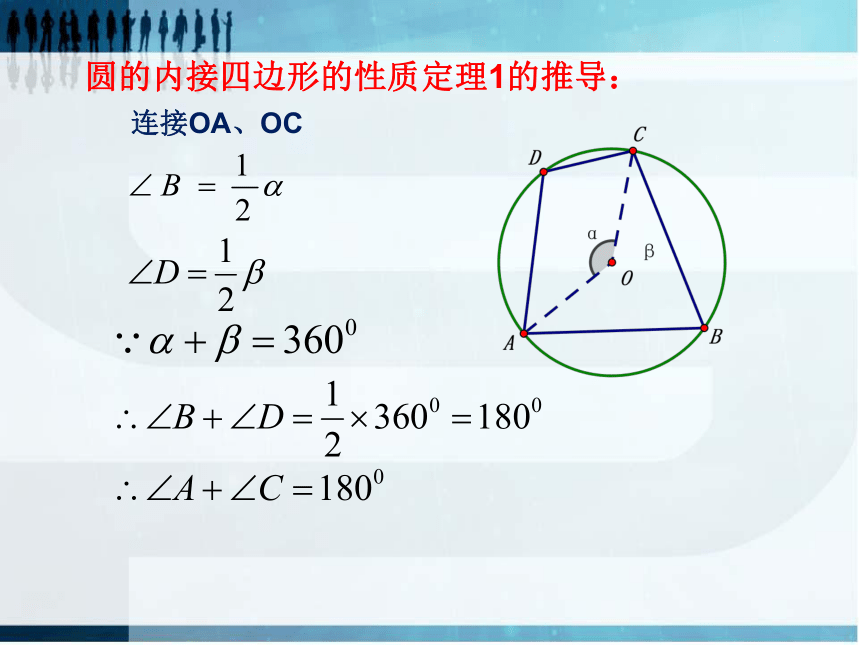
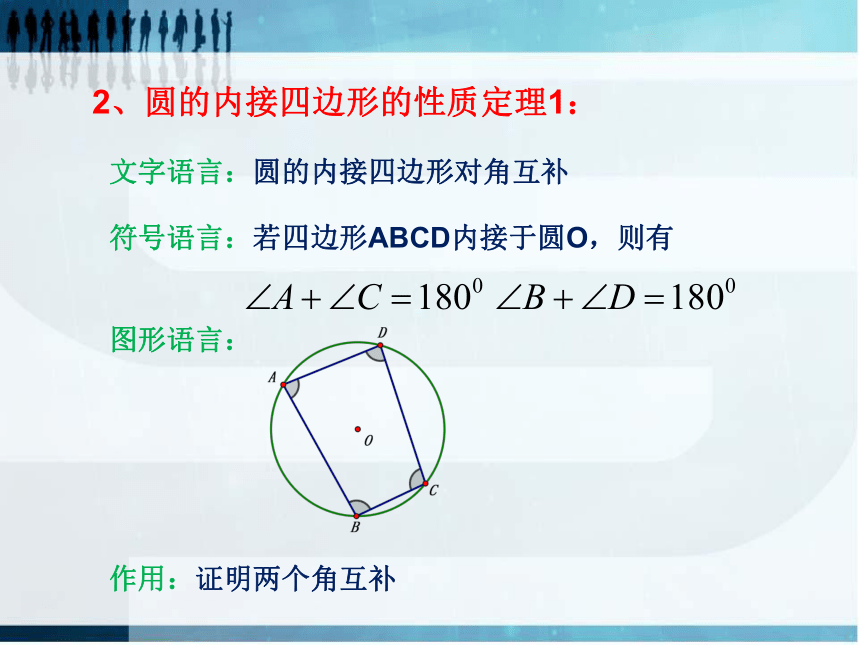
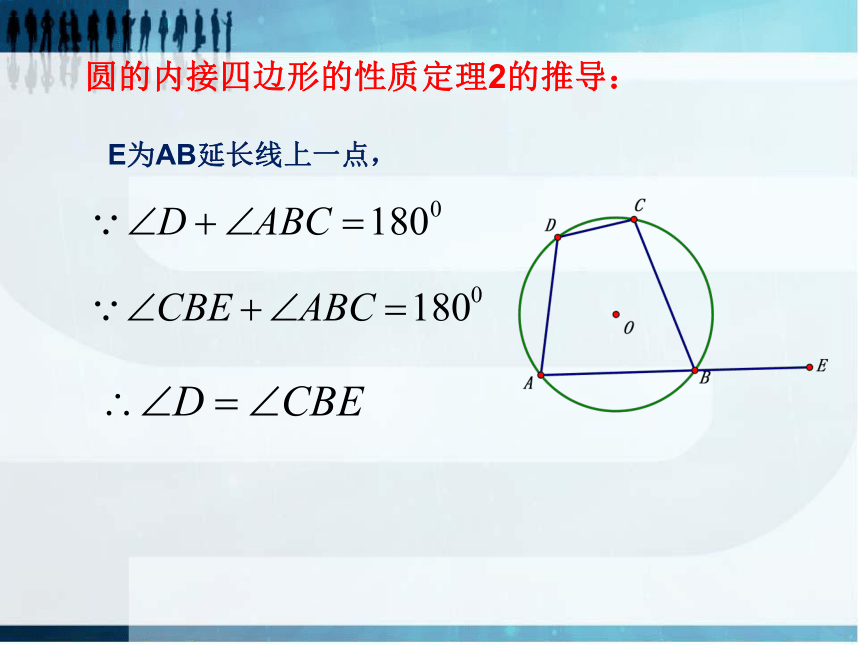
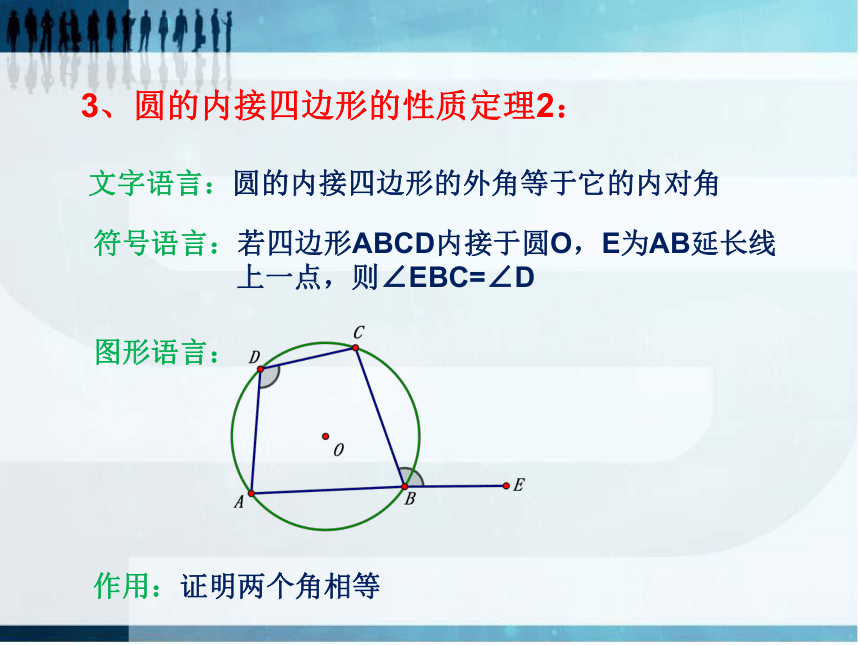
4.任意四边形都有外接圆吗?思考:1.任意三角形都有外接圆,那么任意正方形都有外接圆吗?为什么?2.任意矩形都有外接圆吗?为什么?3.等腰梯形呢?如下四边形都内接于圆这些四边形有什么共同特征?连接OA、OC圆的内接四边形的性质定理1的推导:2、圆的内接四边形的性质定理1:文字语言:圆的内接四边形对角互补符号语言:若四边形ABCD内接于圆O,则有图形语言:作用:证明两个角互补圆的内接四边形的性质定理2的推导:E为AB延长线上一点,3、圆的内接四边形的性质定理2:文字语言:圆的内接四边形的外角等于它的内对角符号语言:若四边形ABCD内接于圆O,E为AB延长线
上一点,则∠EBC=∠D图形语言:作用:证明两个角相等思考:1、圆内接四边形的性质定理1和定理2它们的逆定理是什么?2、逆定理成立吗?如果成立就可以得到四边形存在外接圆的判定定理了分析:不共线的三点A、B、C确定一个外接圆O,如果能证明点D在圆O上,就能够证明四点共圆。点D与圆O有三种位置关系:
(1)点D在圆O上
(2)点D在圆O外
(3)点D在圆O内设AD交圆上于点E,连接CE
假设点D在圆O外这与“三角形的外角大于任一不相邻的内角”矛盾
故点D不可能在圆外反证法延长AD交圆上于点E
假设点D在圆O内这与“三角形的外角大于任一不相邻的内角”矛盾
故点D不可能在圆内4、圆的内接四边形的判定定理:文字语言:如果一个四边形对角互补,那么这个四边
形的四个顶点共圆符号语言:在四边形ABCD中,如果则有图形语言:作用:证明四点共圆或( ),那么A、B、C、D四点共圆5、圆的内接四边形的判定定理推论:文字语言:如果四边形一个外角等于它的内对角,
那么这个四边形的四个顶点共圆图形语言:作用:证明四点共圆请同学们自己证明该定理二、例题讲解及练习例2、如图,CF是 的AB边上的高, ,
.
求证:A、B、P、Q四点共圆练习1、如图,AD、BE是 的两条高.
求证:练习2、求证:对角线互相垂直的四边形中,各边中点在同一个圆周上。三、课堂小结:性质定理1:圆的内接四边形对角互补性质定理2:圆的内接四边形的外角等于它的内对角判定定理:如果一个四边形对角互补,那么这个四边
形的四个顶点共圆判定定理推论:如果四边形一个外角等于它的内对角,
那么这个四边形的四个顶点共圆谢谢大家
2、∠β叫做圆O的
3、∠α与∠β的关系是
4、圆心角的度数等于它所对的 的度数
5、圆周角的度数等于它所对的 的度数
的圆心角弧长一半圆周角弧长二、新知讲解圆内接多边形:所有顶点都在一个圆上的多边形。1.圆内接多边形这个圆称为多边形的外接圆圆内接四边形圆内接五边形
4.任意四边形都有外接圆吗?思考:1.任意三角形都有外接圆,那么任意正方形都有外接圆吗?为什么?2.任意矩形都有外接圆吗?为什么?3.等腰梯形呢?如下四边形都内接于圆这些四边形有什么共同特征?连接OA、OC圆的内接四边形的性质定理1的推导:2、圆的内接四边形的性质定理1:文字语言:圆的内接四边形对角互补符号语言:若四边形ABCD内接于圆O,则有图形语言:作用:证明两个角互补圆的内接四边形的性质定理2的推导:E为AB延长线上一点,3、圆的内接四边形的性质定理2:文字语言:圆的内接四边形的外角等于它的内对角符号语言:若四边形ABCD内接于圆O,E为AB延长线
上一点,则∠EBC=∠D图形语言:作用:证明两个角相等思考:1、圆内接四边形的性质定理1和定理2它们的逆定理是什么?2、逆定理成立吗?如果成立就可以得到四边形存在外接圆的判定定理了分析:不共线的三点A、B、C确定一个外接圆O,如果能证明点D在圆O上,就能够证明四点共圆。点D与圆O有三种位置关系:
(1)点D在圆O上
(2)点D在圆O外
(3)点D在圆O内设AD交圆上于点E,连接CE
假设点D在圆O外这与“三角形的外角大于任一不相邻的内角”矛盾
故点D不可能在圆外反证法延长AD交圆上于点E
假设点D在圆O内这与“三角形的外角大于任一不相邻的内角”矛盾
故点D不可能在圆内4、圆的内接四边形的判定定理:文字语言:如果一个四边形对角互补,那么这个四边
形的四个顶点共圆符号语言:在四边形ABCD中,如果则有图形语言:作用:证明四点共圆或( ),那么A、B、C、D四点共圆5、圆的内接四边形的判定定理推论:文字语言:如果四边形一个外角等于它的内对角,
那么这个四边形的四个顶点共圆图形语言:作用:证明四点共圆请同学们自己证明该定理二、例题讲解及练习例2、如图,CF是 的AB边上的高, ,
.
求证:A、B、P、Q四点共圆练习1、如图,AD、BE是 的两条高.
求证:练习2、求证:对角线互相垂直的四边形中,各边中点在同一个圆周上。三、课堂小结:性质定理1:圆的内接四边形对角互补性质定理2:圆的内接四边形的外角等于它的内对角判定定理:如果一个四边形对角互补,那么这个四边
形的四个顶点共圆判定定理推论:如果四边形一个外角等于它的内对角,
那么这个四边形的四个顶点共圆谢谢大家
