选修4-1 第二讲 直线与圆的位置关系圆内接四边形的性质与判定定理 课件18张PPT
文档属性
| 名称 | 选修4-1 第二讲 直线与圆的位置关系圆内接四边形的性质与判定定理 课件18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 386.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览



文档简介
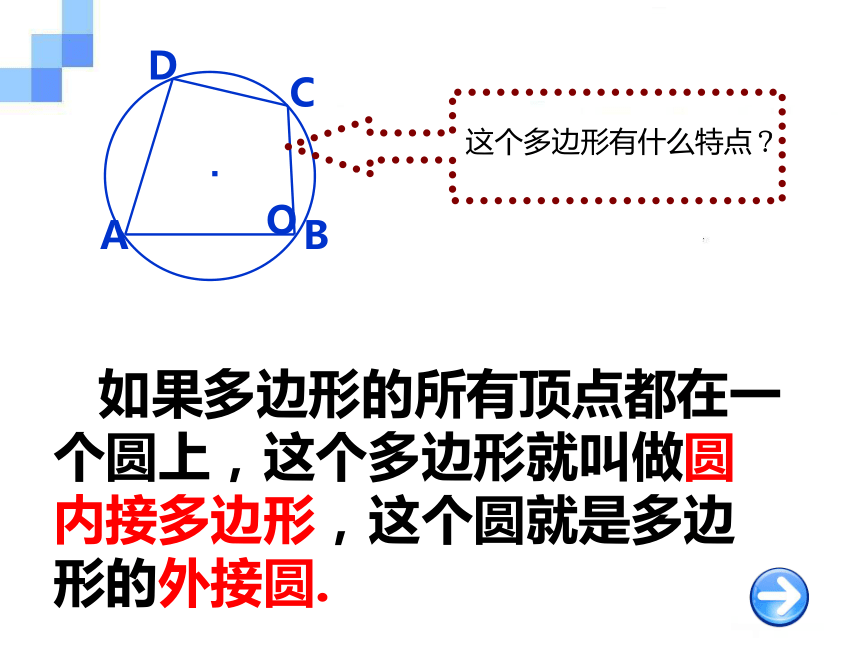
课件18张PPT。 圆内接四边形
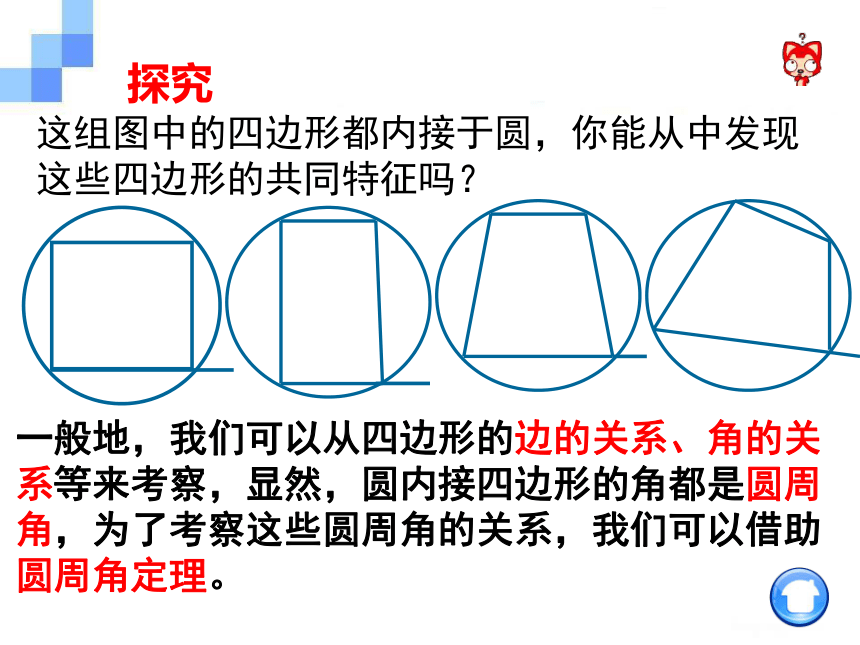
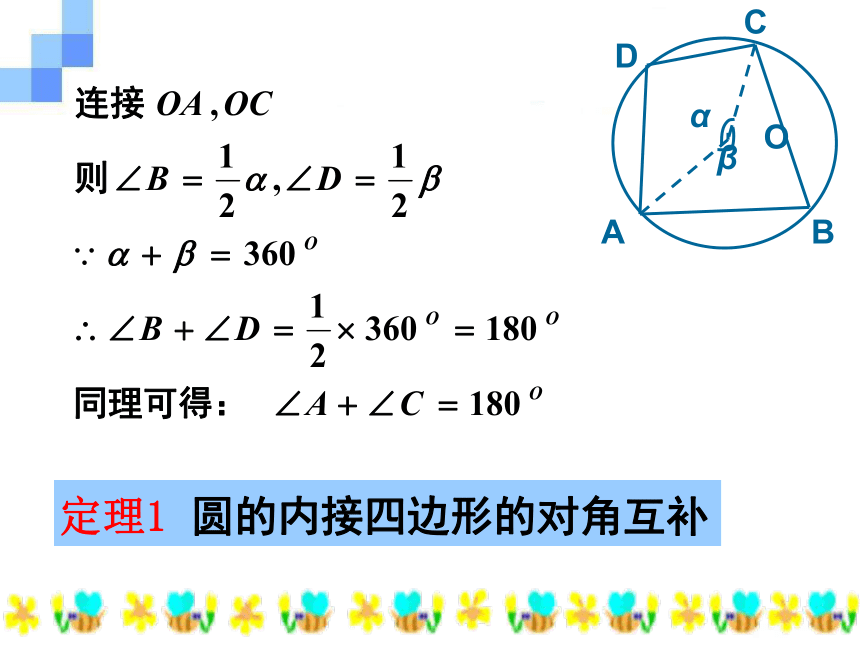
的性质与判定定理普通高中课程标准实验教科书 数 学 选修 4—1 第二讲(二) 理解和掌握圆的内接四边形的性质定理以及判定定理及推论,并能够用性质定理和判定定理解决有关的几何问题. 学习并领会圆的内接四边形性质定理的证明推导过程,应用圆的内接四边形性质解决几何问题过程. 如果多边形的所有顶点都在一个圆上,这个多边形就叫做圆内接多边形,这个圆就是多边形的外接圆. 这组图中的四边形都内接于圆,你能从中发现这些四边形的共同特征吗?一般地,我们可以从四边形的边的关系、角的关系等来考察,显然,圆内接四边形的角都是圆周角,为了考察这些圆周角的关系,我们可以借助圆周角定理。探究ADCBOαβ定理1 圆的内接四边形的对角互补定理2 圆内接四边形的外角等于它的
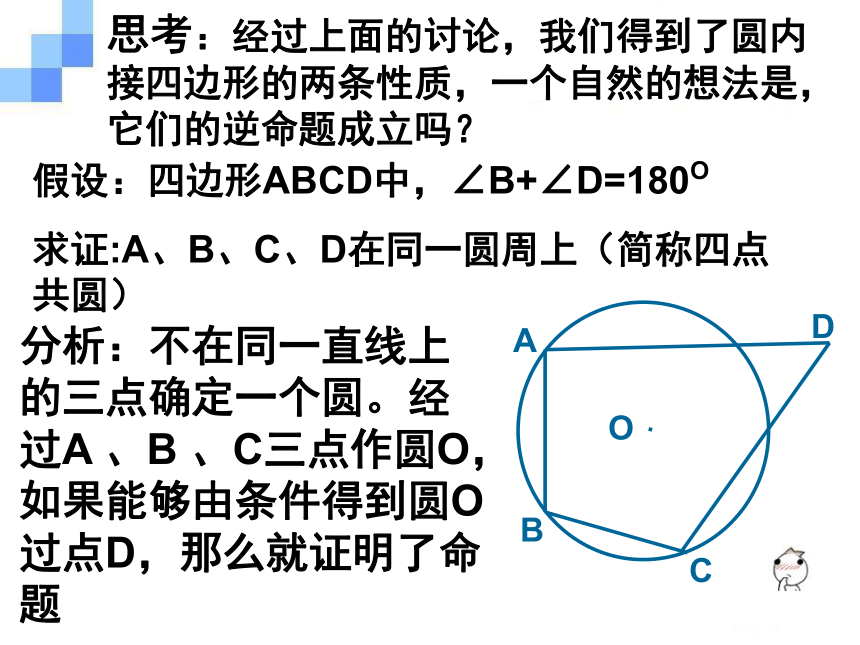
内角的对角.E延长线段AB到点E,观察:?定理1:圆的内接四边形的对角互补。思考:经过上面的讨论,我们得到了圆内接四边形的两条性质,一个自然的想法是,它们的逆命题成立吗?假设:四边形ABCD中,∠B+∠D=180O
求证:A、B、C、D在同一圆周上(简称四点共圆)
分析:不在同一直线上的三点确定一个圆。经过A 、B 、C三点作圆O,如果能够由条件得到圆O过点D,那么就证明了命题E圆O与点D的位置关系:点D在圆外
点D在圆内
点D在圆上若点D在圆外
设E是AD与圆周的交点,连接EC,则有∠AEC+∠B=1800 又∠B+∠D=1800 可得∠D=∠AEC.这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不可能在圆外定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角 若点D在圆内
显然,AD的延长线必与圆相交,设交点为E,连接CE,则∠B+∠E=1800∵∠B+∠ADC=1800
∴∠E=∠ADC
同样产生矛盾
∴点D不可能在圆内
综上所述,点D只能在圆周上,
即A 、B 、C 、D四点共圆。ABCDE定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角o推论如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。圆内接四边形判定定理如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。注意角的位置定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角圆内接四边形判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆
推论:如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。例1:如图,⊙O1与⊙O2都经过A、B两点, 经过点A的直线CD与⊙O1交于点C与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E与⊙O2交于点F。求证:CE∥DF。证明:连接AB∵四边形ABEC是⊙O1的内接四边形∴∠BAD=∠E又∵四边形ADFB是⊙O2的内接四边形∴∠BAD+∠F=1800∴∠E+∠F=1800∴CE∥DF定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角圆内接四边形判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆
推论:如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。例2:如图,CF是△ABC的边AB上的高,FP⊥BC,FQ ⊥AC。
求证:A、B、P、Q四点共圆。证明:连接PQ在四边形QFPC中,∵ FP⊥BC,FQ ⊥AC∴∠FQA=∠FPC又∵CF⊥AB∴Q、F、P、C四点共圆∴∠QFC=∠QPC∴∠QFC与∠QFA互余。∴∠A=∠QFC∴∠A=∠QPC∴A、B、P、Q四点共圆小结:圆的内接四边形的对角互补。圆内接四边形判定定理推论圆内接四边形的外角等于它的内角的对角。定理1定理2 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。
如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。1、如图,AD、BE是△ABC的两条高,
求证:∠CED=∠ABCOF练习2、求证:对角线互相垂直的四边形中,各边中点在同一个圆周上。练习3、如图:已知四边形ABCD内接于圆,延长AB和DC相交于E,EG平分∠E,且与BC、AD分别交于F、G。求证: ∠ CFG=∠DGF练习作业 如果四边形一边上的两个顶点的视角相等,那么四边形的四个顶点共圆作业一作业二预习圆的切线的性质及判定定理www.themegallery.com谢谢
求证:A、B、C、D在同一圆周上(简称四点共圆)
分析:不在同一直线上的三点确定一个圆。经过A 、B 、C三点作圆O,如果能够由条件得到圆O过点D,那么就证明了命题E圆O与点D的位置关系:点D在圆外
点D在圆内
点D在圆上若点D在圆外
设E是AD与圆周的交点,连接EC,则有∠AEC+∠B=1800 又∠B+∠D=1800 可得∠D=∠AEC.这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不可能在圆外定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角 若点D在圆内
显然,AD的延长线必与圆相交,设交点为E,连接CE,则∠B+∠E=1800∵∠B+∠ADC=1800
∴∠E=∠ADC
同样产生矛盾
∴点D不可能在圆内
综上所述,点D只能在圆周上,
即A 、B 、C 、D四点共圆。ABCDE定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角o推论如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。圆内接四边形判定定理如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。注意角的位置定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角圆内接四边形判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆
推论:如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。例1:如图,⊙O1与⊙O2都经过A、B两点, 经过点A的直线CD与⊙O1交于点C与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E与⊙O2交于点F。求证:CE∥DF。证明:连接AB∵四边形ABEC是⊙O1的内接四边形∴∠BAD=∠E又∵四边形ADFB是⊙O2的内接四边形∴∠BAD+∠F=1800∴∠E+∠F=1800∴CE∥DF定理1:圆的内接四边形的对角互补。定理2:圆内接四边形的外角等于它的内角的对角圆内接四边形判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆
推论:如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。例2:如图,CF是△ABC的边AB上的高,FP⊥BC,FQ ⊥AC。
求证:A、B、P、Q四点共圆。证明:连接PQ在四边形QFPC中,∵ FP⊥BC,FQ ⊥AC∴∠FQA=∠FPC又∵CF⊥AB∴Q、F、P、C四点共圆∴∠QFC=∠QPC∴∠QFC与∠QFA互余。∴∠A=∠QFC∴∠A=∠QPC∴A、B、P、Q四点共圆小结:圆的内接四边形的对角互补。圆内接四边形判定定理推论圆内接四边形的外角等于它的内角的对角。定理1定理2 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。
如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆。1、如图,AD、BE是△ABC的两条高,
求证:∠CED=∠ABCOF练习2、求证:对角线互相垂直的四边形中,各边中点在同一个圆周上。练习3、如图:已知四边形ABCD内接于圆,延长AB和DC相交于E,EG平分∠E,且与BC、AD分别交于F、G。求证: ∠ CFG=∠DGF练习作业 如果四边形一边上的两个顶点的视角相等,那么四边形的四个顶点共圆作业一作业二预习圆的切线的性质及判定定理www.themegallery.com谢谢
