选修4-1 第二讲 直线与圆的位置关系圆的切线的性质及判定定理课件17张PPT
文档属性
| 名称 | 选修4-1 第二讲 直线与圆的位置关系圆的切线的性质及判定定理课件17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览

文档简介
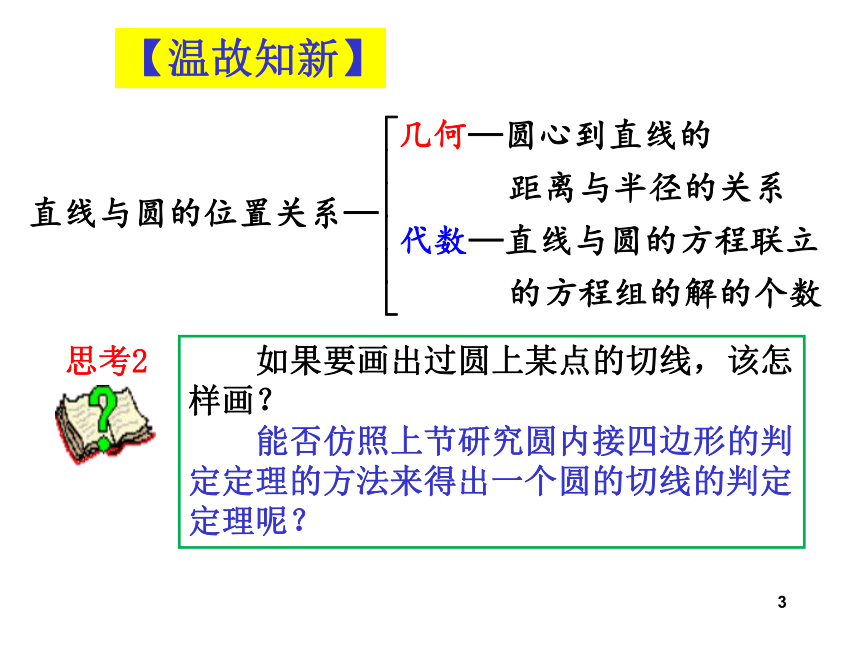
课件17张PPT。2.3 圆的切线的性质
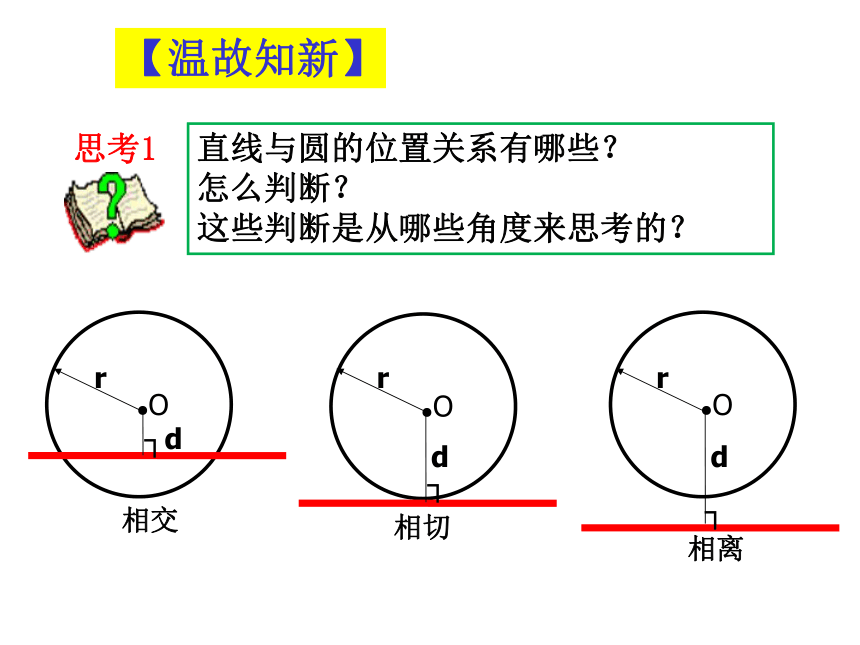
及判定定理【温故知新】【温故知新】切线
的性质切线的
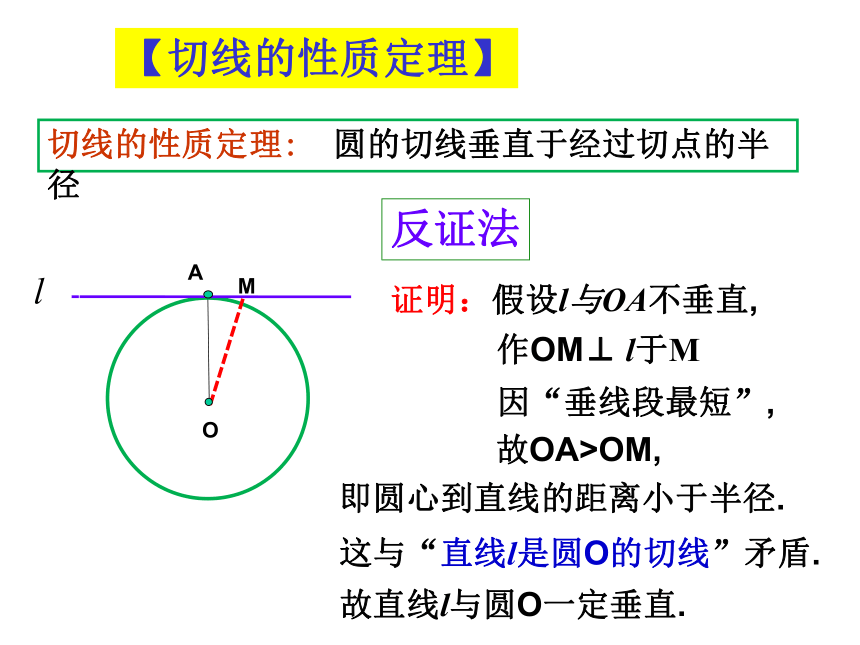
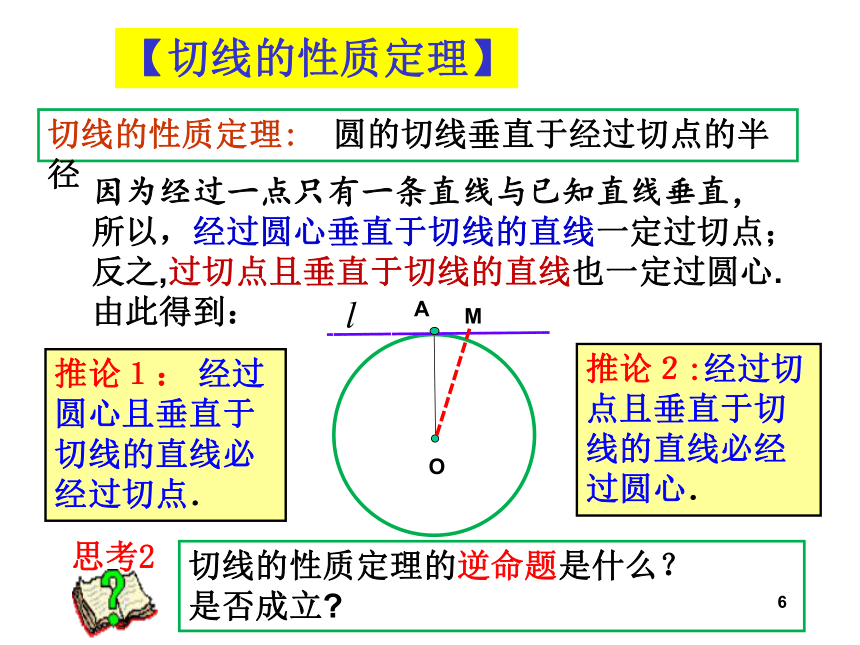
判定定理【温故知新】O反证法这与“直线l是圆O的切线”矛盾.切线的性质定理: 圆的切线垂直于经过切点的半径证明:假设l与OA不垂直,作OM⊥ l于M因“垂线段最短”,故OA>OM,即圆心到直线的距离小于半径.A故直线l与圆O一定垂直.【切线的性质定理】因为经过一点只有一条直线与已知直线垂直,所以,经过圆心垂直于切线的直线一定过切点;反之,过切点且垂直于切线的直线也一定过圆心.由此得到:推论1: 经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.切线的性质定理: 圆的切线垂直于经过切点的半径【切线的性质定理】切线的判定定理:
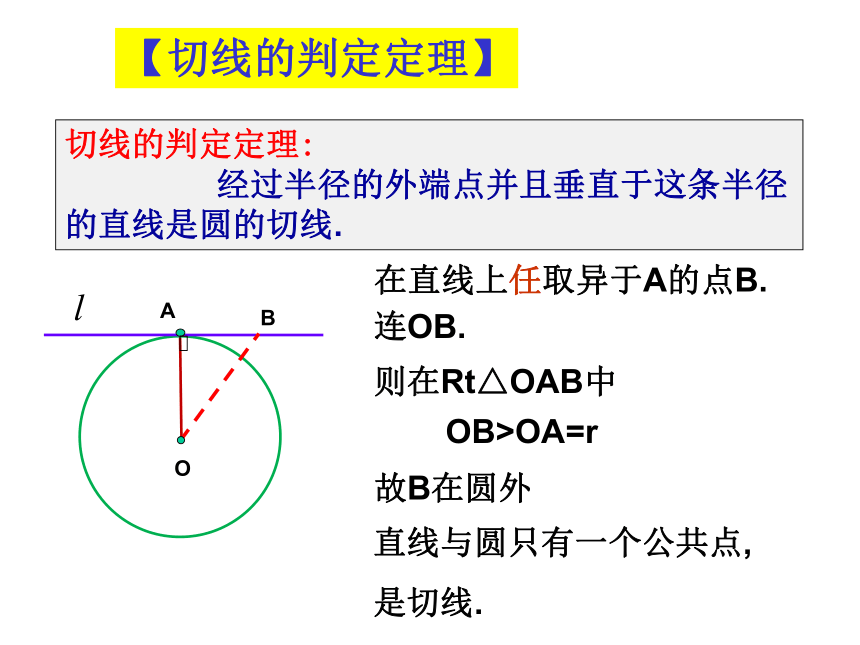
经过半径的外端点并且垂直于这条半径的直线是圆的切线.AOB直线与圆只有一个公共点,是切线.在直线上任取异于A的点B.连OB.则在Rt△OAB中OB>OA=r故B在圆外【切线的判定定理】例1 如图,AB是⊙O的直径, ⊙O过BC的中点D,
DE⊥AC.求证:DE是⊙O是切线.证明:连接OD. ∴OD是△ABC的中位线,∴OD//AC.又∵∠DEC=90o∴∠ODE=90o又∵D在圆周上,OD是半径∴DE是⊙O的切线..∵BD=CD,OA=OB,【例题解析】例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过C点的切线互相垂直,垂足为 D,求证:AC平分∠DAB.证明:连接OC, ∴OC⊥CD.又∵AD⊥CD,∴OC//AD.∵OC=OA.∴ ∠CAO=∠ACO.∴ ∠CAD=∠CAO.故AC平分∠DAB.∵CD是⊙O的切线,由此得 ∠ACO=∠CAD.【例题解析】例3 作经过一定点C的圆的切线.(1)点C在圆上.(2)点C在圆外.作法:连接OC,过点C作AB⊥OC.则直线AB就是所要作的切线.作法:连接OC,以OC为直径的圆为⊙O1,与⊙O 相交于两点P和P′.连接CP和CP′,则CP和CP′都是过已知点C所引⊙O的切线.你能
证明吗?【例题解析】练习1.如图A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且AB=BC,∠C=30°. 求证:直线AB是⊙O的切线.证明:连结OB,∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°
∴ AB是⊙O的切线.题目中“半径”已有,
只需证“垂直”,即可
得直线与圆相切.【巩固练习】∵AO=OC,
∴∠OCA=∠A=30°,
∴∠BOC=60°.
∴△BOC是等边三角形. ∴BD=OB=BC,
∠D=∠BCD=30°. ∴∠DCO=90°. ∴DC⊥OC.
∴DC是⊙O的切线.练习2.已知:如图,AB是⊙O的直径,D在AB的延长线上,BD=OB,C在圆上,∠CAB=30°,求证:DC是⊙O的切线.证明:连OC、BC,【巩固练习】练习3 若Rt△ABC内接于⊙O,∠A=30°.延长斜边AB到D,使BD等于⊙O的半径,求证:DC是⊙O的切线.1200600600600分析:如图【巩固练习】习题2.31.如图,△ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D.求证:AC与⊙O相切.2.已知:OA和OB是⊙O的半径,并且OA⊥OB,P是OA
上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切
线交OA的延长线于R,.求证:RP=RQBOPARQ∠AQO= ∠APQ3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.AOBCD1324△COD与COB全等思考:
当P由圆内移动到圆外是,有何结论?⌒AD的度数与BC的度数和的一半等于∠APD的度数.DACBPE⌒AB与CD相交于圆内一点P.∴ ∠P= ∠BAC- ∠ACP圆内角定理:且∠BAC= ∠P+ ∠ACP
及判定定理【温故知新】【温故知新】切线
的性质切线的
判定定理【温故知新】O反证法这与“直线l是圆O的切线”矛盾.切线的性质定理: 圆的切线垂直于经过切点的半径证明:假设l与OA不垂直,作OM⊥ l于M因“垂线段最短”,故OA>OM,即圆心到直线的距离小于半径.A故直线l与圆O一定垂直.【切线的性质定理】因为经过一点只有一条直线与已知直线垂直,所以,经过圆心垂直于切线的直线一定过切点;反之,过切点且垂直于切线的直线也一定过圆心.由此得到:推论1: 经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.切线的性质定理: 圆的切线垂直于经过切点的半径【切线的性质定理】切线的判定定理:
经过半径的外端点并且垂直于这条半径的直线是圆的切线.AOB直线与圆只有一个公共点,是切线.在直线上任取异于A的点B.连OB.则在Rt△OAB中OB>OA=r故B在圆外【切线的判定定理】例1 如图,AB是⊙O的直径, ⊙O过BC的中点D,
DE⊥AC.求证:DE是⊙O是切线.证明:连接OD. ∴OD是△ABC的中位线,∴OD//AC.又∵∠DEC=90o∴∠ODE=90o又∵D在圆周上,OD是半径∴DE是⊙O的切线..∵BD=CD,OA=OB,【例题解析】例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过C点的切线互相垂直,垂足为 D,求证:AC平分∠DAB.证明:连接OC, ∴OC⊥CD.又∵AD⊥CD,∴OC//AD.∵OC=OA.∴ ∠CAO=∠ACO.∴ ∠CAD=∠CAO.故AC平分∠DAB.∵CD是⊙O的切线,由此得 ∠ACO=∠CAD.【例题解析】例3 作经过一定点C的圆的切线.(1)点C在圆上.(2)点C在圆外.作法:连接OC,过点C作AB⊥OC.则直线AB就是所要作的切线.作法:连接OC,以OC为直径的圆为⊙O1,与⊙O 相交于两点P和P′.连接CP和CP′,则CP和CP′都是过已知点C所引⊙O的切线.你能
证明吗?【例题解析】练习1.如图A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且AB=BC,∠C=30°. 求证:直线AB是⊙O的切线.证明:连结OB,∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°
∴ AB是⊙O的切线.题目中“半径”已有,
只需证“垂直”,即可
得直线与圆相切.【巩固练习】∵AO=OC,
∴∠OCA=∠A=30°,
∴∠BOC=60°.
∴△BOC是等边三角形. ∴BD=OB=BC,
∠D=∠BCD=30°. ∴∠DCO=90°. ∴DC⊥OC.
∴DC是⊙O的切线.练习2.已知:如图,AB是⊙O的直径,D在AB的延长线上,BD=OB,C在圆上,∠CAB=30°,求证:DC是⊙O的切线.证明:连OC、BC,【巩固练习】练习3 若Rt△ABC内接于⊙O,∠A=30°.延长斜边AB到D,使BD等于⊙O的半径,求证:DC是⊙O的切线.1200600600600分析:如图【巩固练习】习题2.31.如图,△ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D.求证:AC与⊙O相切.2.已知:OA和OB是⊙O的半径,并且OA⊥OB,P是OA
上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切
线交OA的延长线于R,.求证:RP=RQBOPARQ∠AQO= ∠APQ3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.AOBCD1324△COD与COB全等思考:
当P由圆内移动到圆外是,有何结论?⌒AD的度数与BC的度数和的一半等于∠APD的度数.DACBPE⌒AB与CD相交于圆内一点P.∴ ∠P= ∠BAC- ∠ACP圆内角定理:且∠BAC= ∠P+ ∠ACP
