选修4-1 第二讲 直线与圆的位置关系 圆的切线的性质及判定定理 课件36张PPT
文档属性
| 名称 | 选修4-1 第二讲 直线与圆的位置关系 圆的切线的性质及判定定理 课件36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 449.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览






文档简介
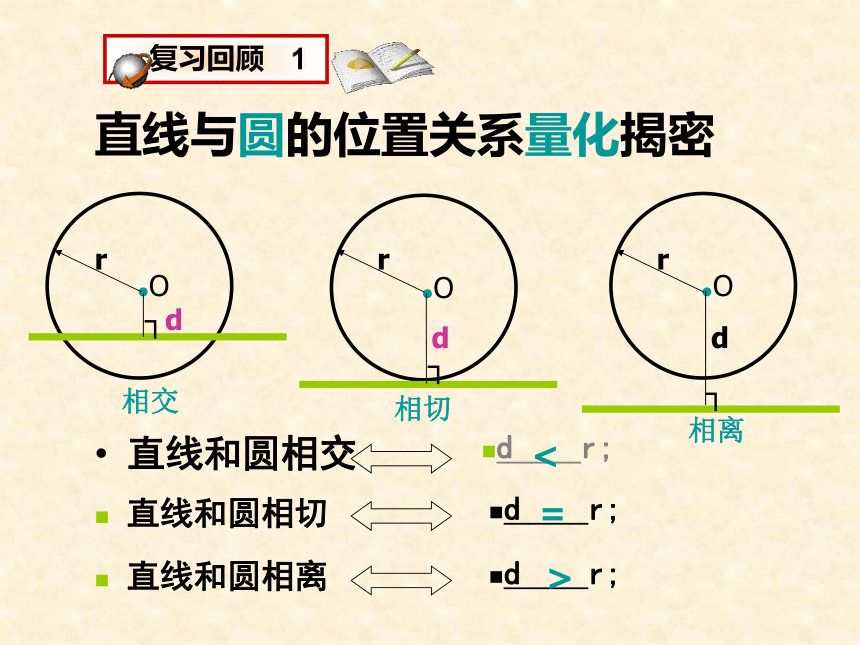
课件36张PPT。切线的性质直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>切线的性质:
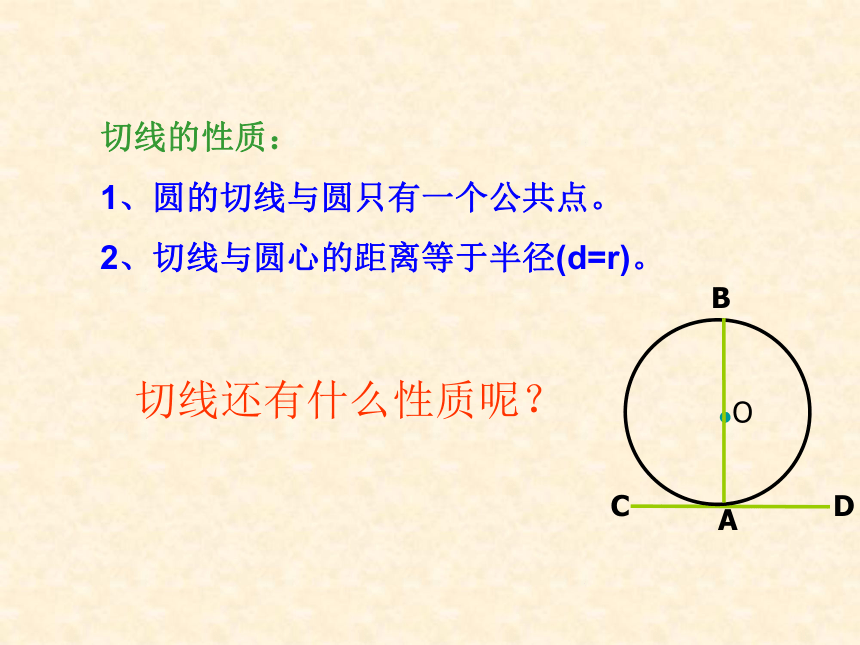
1、圆的切线与圆只有一个公共点。
2、切线与圆心的距离等于半径(d=r)。切线还有什么性质呢?探索切线性质如图,直线CD与⊙O相切于点A, 半径OA与直线CD有怎样的位置关系?说说你的理由.半径OA垂直于直线CD.老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,OA所在直线是对称轴,
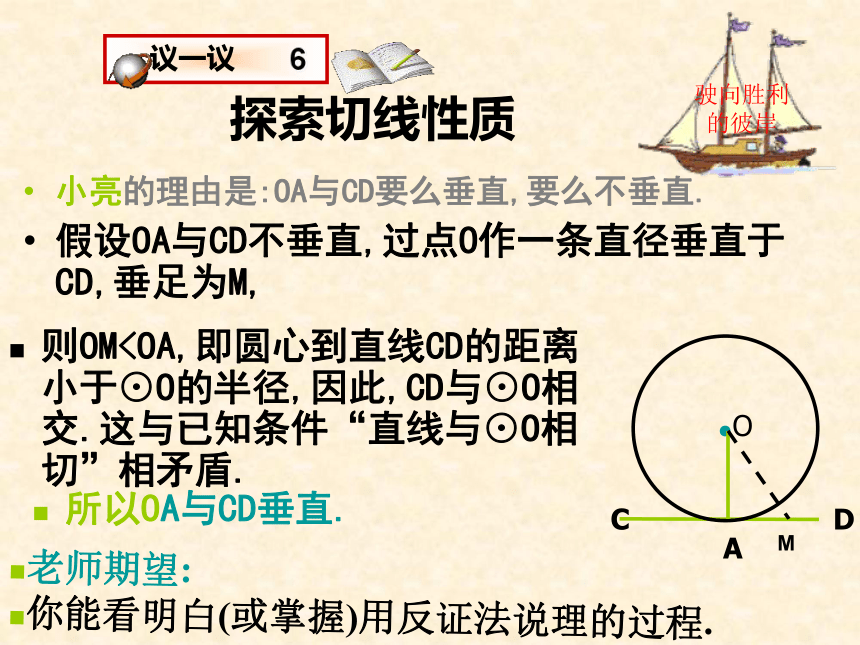
∴沿它对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.CD●OA探索切线性质小亮的理由是:OA与CD要么垂直,要么不垂直.假设OA与CD不垂直,过点O作一条直径垂直于CD,垂足为M,老师期望:
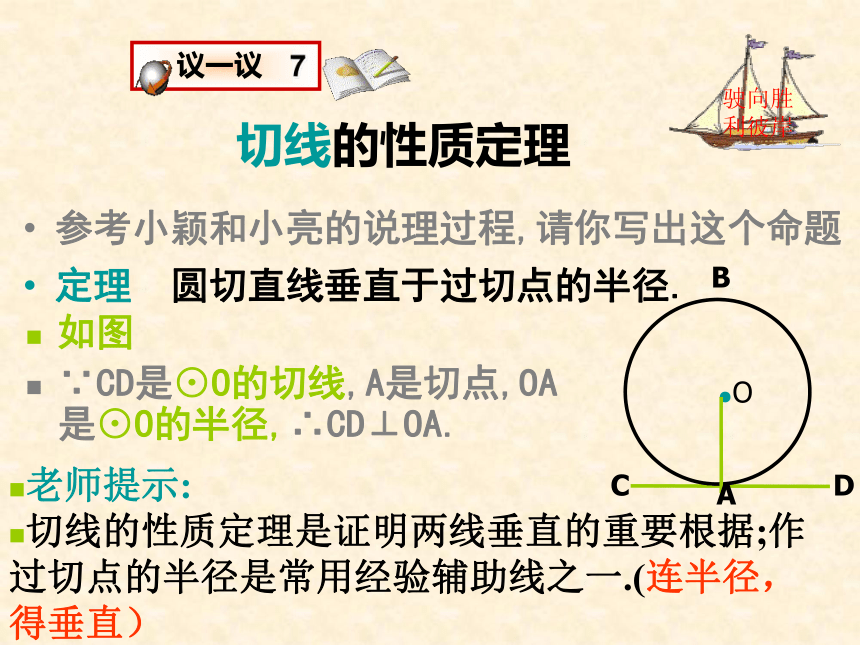
你能看明白(或掌握)用反证法说理的过程.则OM切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.(连半径,得垂直)如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.CDB●OA一、切线的性质:
1、圆的切线与圆只有一个公共点。
2、切线与圆心的距离等于半径(d=r)。
3、圆的切线垂直于过切点的半径。二、辅助线的作法
作过切点的半径(连半径,得垂直)
切线的性质定理的应用切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长. 切线的判定:
1、直线与圆公共点的个数:只有一个公共点。
2、圆心到直线的距离与半径的大小关系,即d=r。
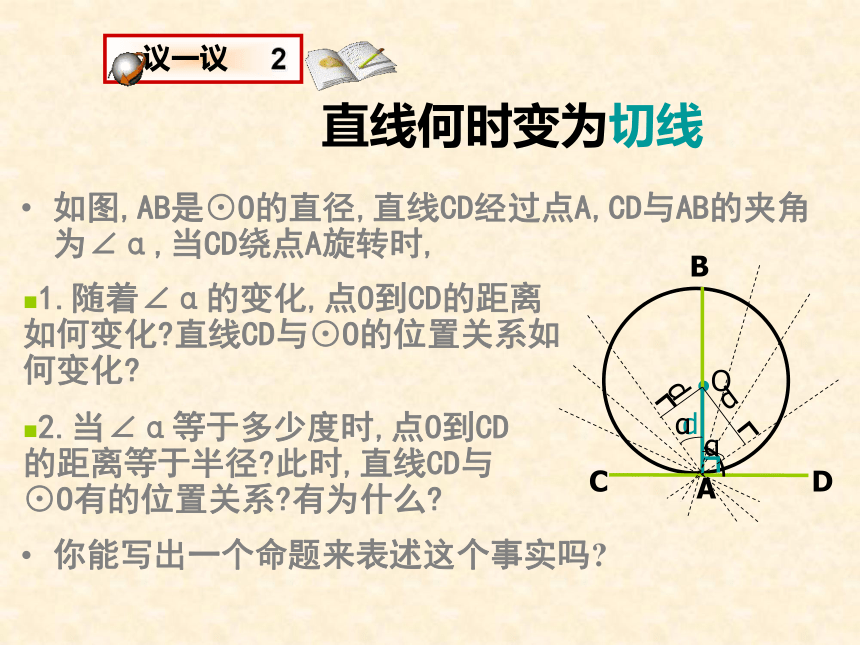
还有其它方法吗?直线何时变为切线如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,你能写出一个命题来表述这个事实吗?1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?切线的判定定理定理 经过半径的外端且垂直于这条半径的直线是圆的切线.老师提示:
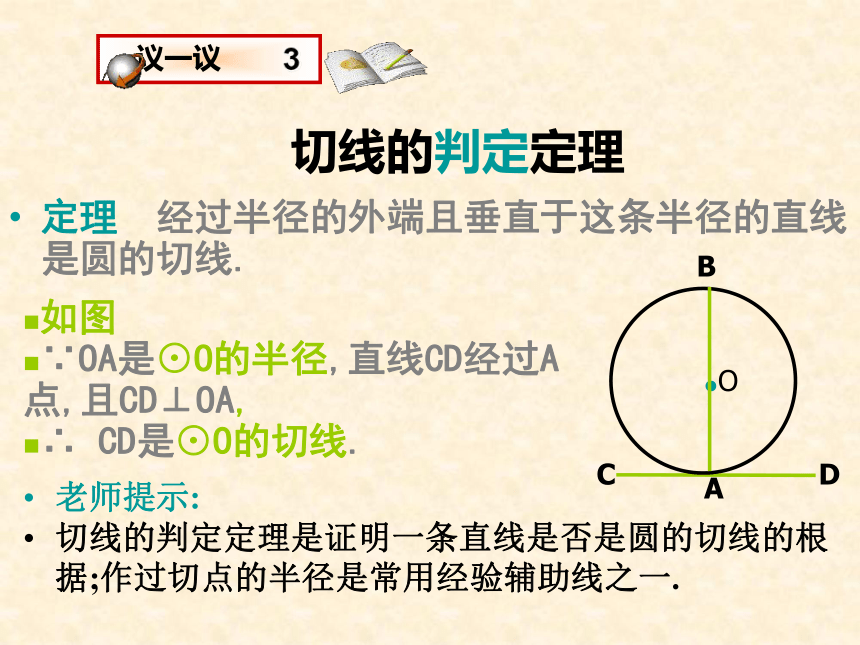
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.切线的判定:
1、直线与圆公共点的个数:只有一个公共点。
2、圆心到直线的距离与半径的大小关系,即d=r。
3、经过半径外端且垂直于这条半径的直线是圆的切线。切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端且垂直于这条半径的直线是圆的切线”只要连结OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?练习与巩固:2、如图,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于点D,与AB相交于点E,则∠ADE等于___ _度. 1、如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A. 70° B. 35° C. 20° D. 10°(2)(1)3、如图,在△OAB中,OB:AB=3:2 , 0B=6,⊙O与AB相切于点A, 则⊙O的直径为 。OAB(3)4、如图,PA、PB是⊙O的切线,切点分别为A、B,且∠APB=50°,点C是优弧上的一点,则∠ACB=___.5、如图,⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为( )
A. B. C. 10 D. 5 (5)(4)辅助线的作法:作过切点的半径7、如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB。(7)8、如图,AB为⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,求证:CD是⊙O的切线。(8)1、确定一个圆的位置与大小的条件是什么? 圆心与半径2、角平分线的性质定理与判定定理性质:在一个角的内部,角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。1.经过三角形三个顶点可以作一个圆。
2.经过三角形各顶点的圆叫做
三角形的外接圆。
3.三角形外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形。三角形与圆的位置关系(回顾)BCOA性质:三角形的外心到三角形三个顶点的距离相等 如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢? 三角形的外接圆在实际中很有用,但还有用它不能解决的问题.如三角形的内切圆Or思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线
BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN试一试:
你能画出一个三角形的内切圆吗?定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心,这个三角形叫做圆的外切三角形。1.三角形的内心到三角形各边的距离相等;性质:Or2.三角形的内心在三角形的角平分线上; 1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三条角平分线 3. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在三角形的_______. 1无数内部思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线
BE和CF,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 EF试一试:
你能画出一个三角形的内切圆吗?这样的圆可以作出几个呢?为什么?.∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.IEFABC定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。1.三角形的内心到三角形各边的距离相等;性质:Or2.三角形的内心在三角形的角平分线上; 分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?提示:先确定圆心和半径,尺规作图要保留作图痕迹. 1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三条角平分线 3. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在三角形的_______. 1无数内部
例2 如图,在△ABC中,点I是内心, (1)若∠ABC=50°, ∠ACB=70°,
求∠BIC的度数(2)若∠A=68度,则∠BIC=
(3)若∠BIC=110度,则∠A=
(4) ∠BIC和∠A的关系 判断题:
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
错错对4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
对 错 对探索:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?I●I●上右图就是三角形的内切圆作法:D(1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求MN
1、圆的切线与圆只有一个公共点。
2、切线与圆心的距离等于半径(d=r)。切线还有什么性质呢?探索切线性质如图,直线CD与⊙O相切于点A, 半径OA与直线CD有怎样的位置关系?说说你的理由.半径OA垂直于直线CD.老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,OA所在直线是对称轴,
∴沿它对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.CD●OA探索切线性质小亮的理由是:OA与CD要么垂直,要么不垂直.假设OA与CD不垂直,过点O作一条直径垂直于CD,垂足为M,老师期望:
你能看明白(或掌握)用反证法说理的过程.则OM
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.CDB●OA一、切线的性质:
1、圆的切线与圆只有一个公共点。
2、切线与圆心的距离等于半径(d=r)。
3、圆的切线垂直于过切点的半径。二、辅助线的作法
作过切点的半径(连半径,得垂直)
切线的性质定理的应用切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长. 切线的判定:
1、直线与圆公共点的个数:只有一个公共点。
2、圆心到直线的距离与半径的大小关系,即d=r。
还有其它方法吗?直线何时变为切线如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,你能写出一个命题来表述这个事实吗?1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?切线的判定定理定理 经过半径的外端且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.切线的判定:
1、直线与圆公共点的个数:只有一个公共点。
2、圆心到直线的距离与半径的大小关系,即d=r。
3、经过半径外端且垂直于这条半径的直线是圆的切线。切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端且垂直于这条半径的直线是圆的切线”只要连结OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?练习与巩固:2、如图,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于点D,与AB相交于点E,则∠ADE等于___ _度. 1、如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A. 70° B. 35° C. 20° D. 10°(2)(1)3、如图,在△OAB中,OB:AB=3:2 , 0B=6,⊙O与AB相切于点A, 则⊙O的直径为 。OAB(3)4、如图,PA、PB是⊙O的切线,切点分别为A、B,且∠APB=50°,点C是优弧上的一点,则∠ACB=___.5、如图,⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为( )
A. B. C. 10 D. 5 (5)(4)辅助线的作法:作过切点的半径7、如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB。(7)8、如图,AB为⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,求证:CD是⊙O的切线。(8)1、确定一个圆的位置与大小的条件是什么? 圆心与半径2、角平分线的性质定理与判定定理性质:在一个角的内部,角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。1.经过三角形三个顶点可以作一个圆。
2.经过三角形各顶点的圆叫做
三角形的外接圆。
3.三角形外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形。三角形与圆的位置关系(回顾)BCOA性质:三角形的外心到三角形三个顶点的距离相等 如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢? 三角形的外接圆在实际中很有用,但还有用它不能解决的问题.如三角形的内切圆Or思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线
BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN试一试:
你能画出一个三角形的内切圆吗?定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心,这个三角形叫做圆的外切三角形。1.三角形的内心到三角形各边的距离相等;性质:Or2.三角形的内心在三角形的角平分线上; 1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三条角平分线 3. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在三角形的_______. 1无数内部思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线
BE和CF,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 EF试一试:
你能画出一个三角形的内切圆吗?这样的圆可以作出几个呢?为什么?.∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.IEFABC定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。1.三角形的内心到三角形各边的距离相等;性质:Or2.三角形的内心在三角形的角平分线上; 分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?提示:先确定圆心和半径,尺规作图要保留作图痕迹. 1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三条角平分线 3. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在三角形的_______. 1无数内部
例2 如图,在△ABC中,点I是内心, (1)若∠ABC=50°, ∠ACB=70°,
求∠BIC的度数(2)若∠A=68度,则∠BIC=
(3)若∠BIC=110度,则∠A=
(4) ∠BIC和∠A的关系 判断题:
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
错错对4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
对 错 对探索:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?I●I●上右图就是三角形的内切圆作法:D(1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求MN
