选修4-1 第二讲 直线与圆的位置关系 弦切角的性质 课件 45张PPT
文档属性
| 名称 | 选修4-1 第二讲 直线与圆的位置关系 弦切角的性质 课件 45张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 422.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 20:56:00 | ||
图片预览



文档简介
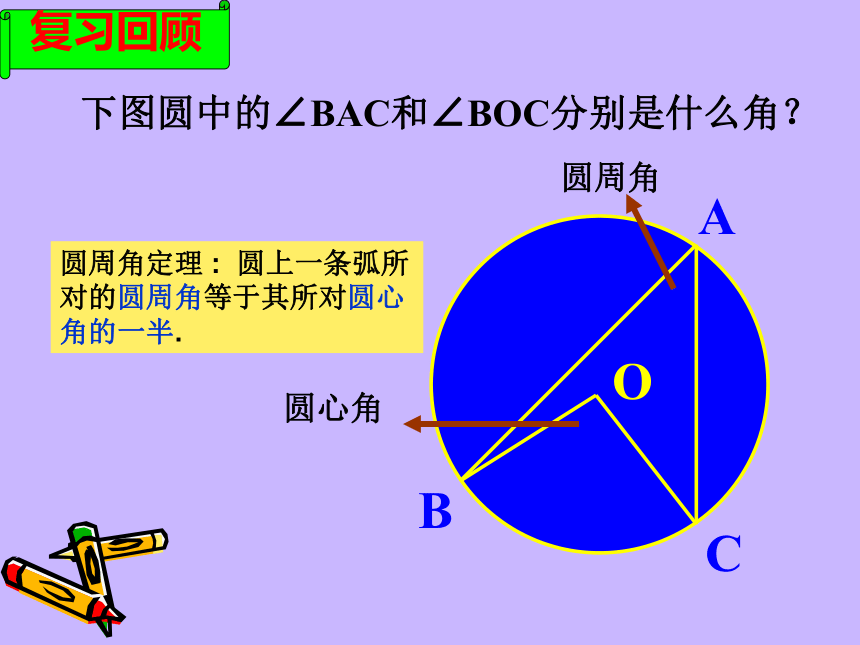
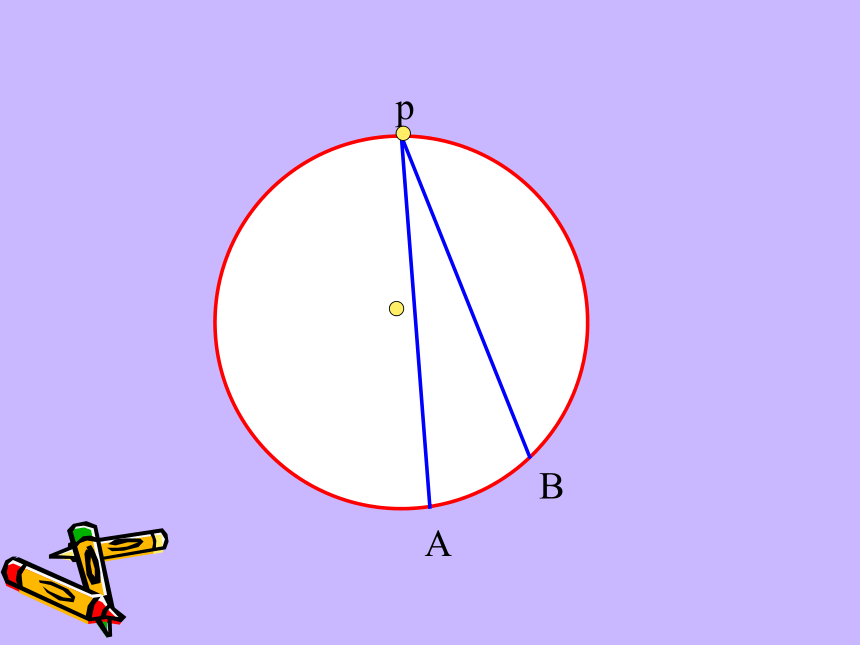
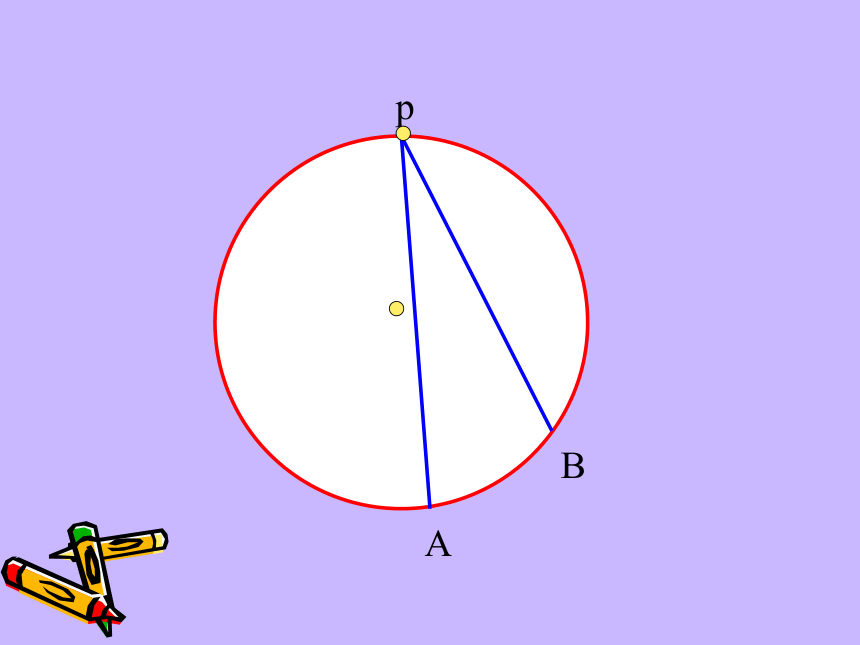
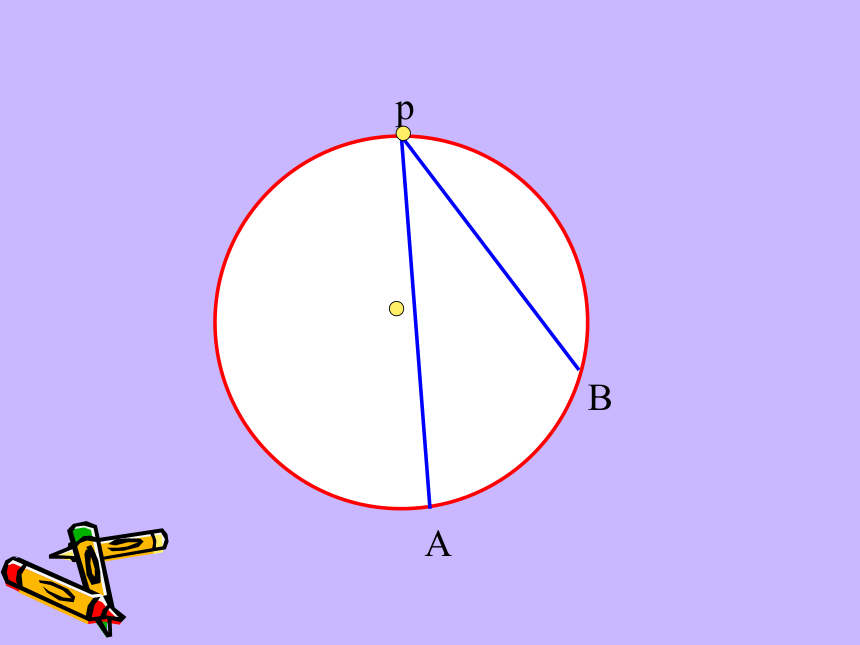
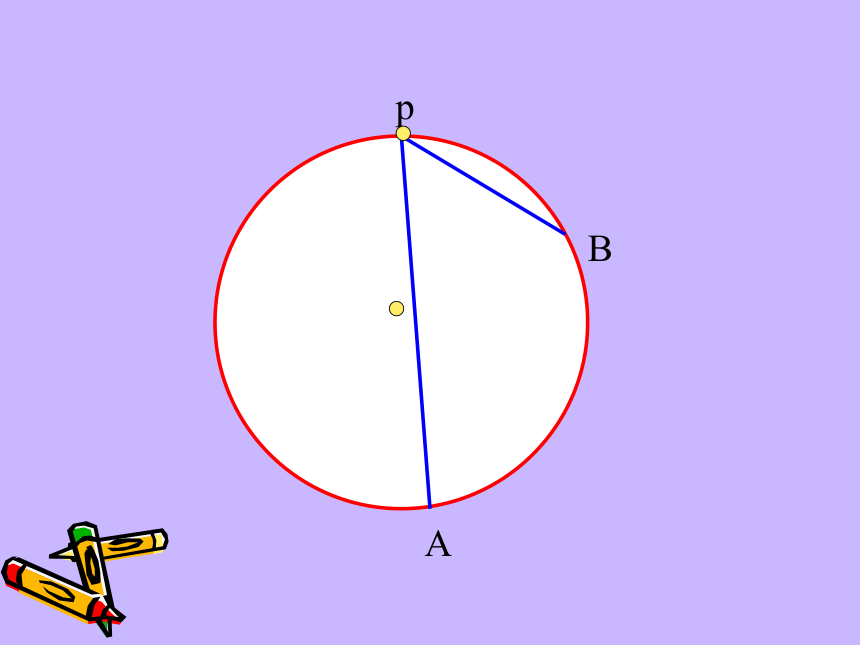
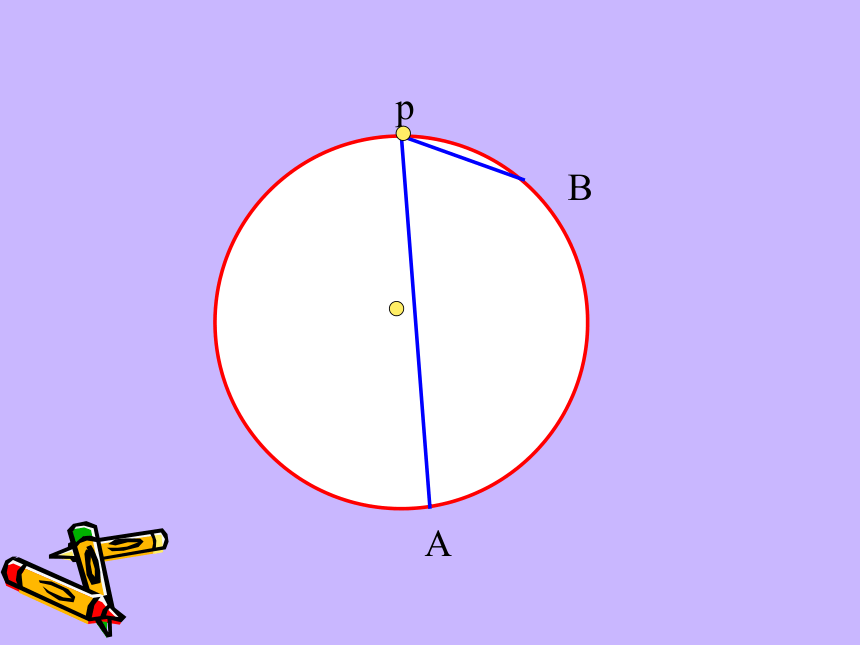
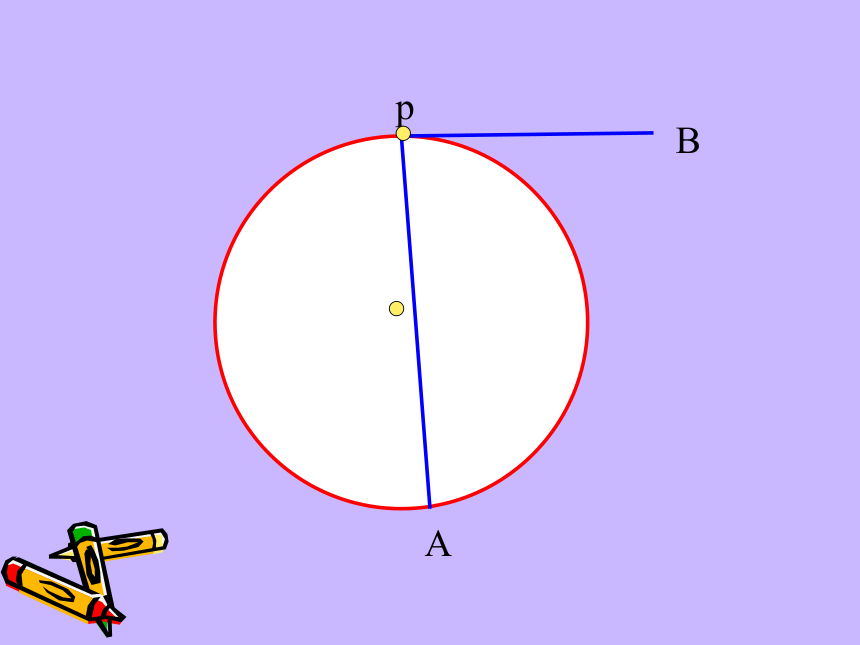
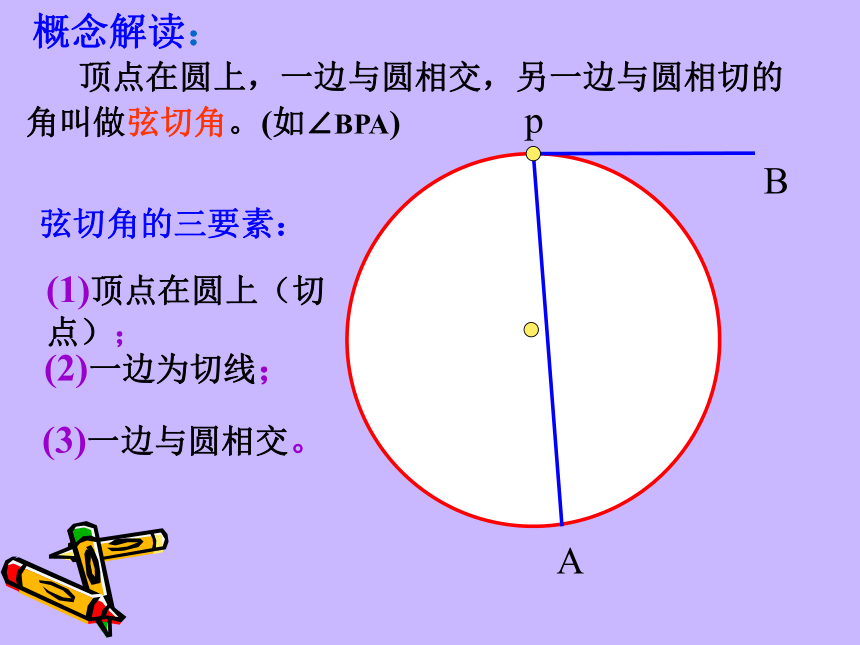
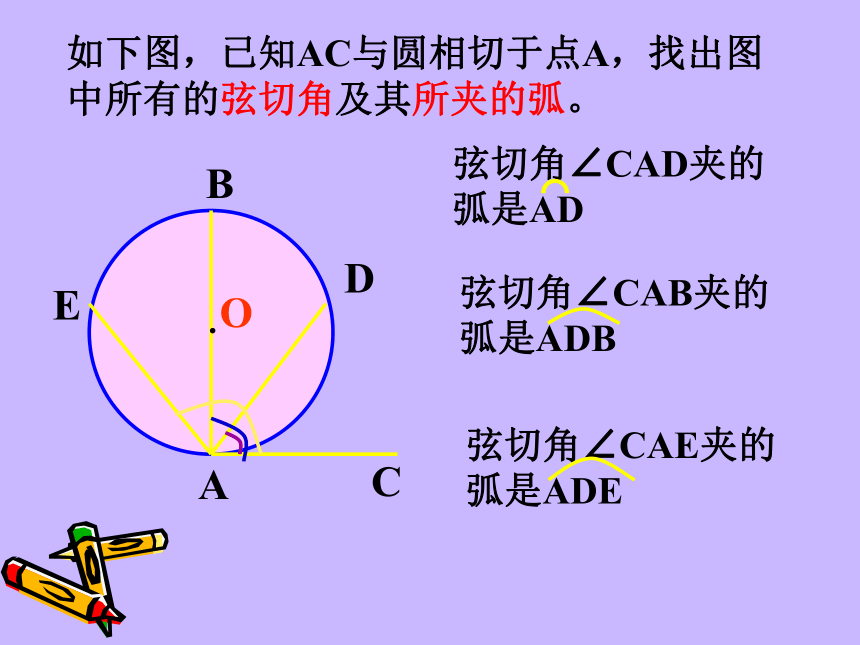
课件45张PPT。弦切角的性质复习回顾 下图圆中的∠BAC和∠BOC分别是什么角?圆周角定理 : 圆上一条弧所对的圆周角等于其所对圆心角的一半.圆周角圆心角 pAB pAB pAB pAB pAB pAB pAB pAB 顶点在圆上,一边与圆相交,另一边与圆相切的角叫做弦切角。(如∠BPA)(1)顶点在圆上(切点);(2)一边为切线;(3)一边与圆相交。弦切角的三要素:概念解读:AAAAABBBBBCCCCC下面五个图中的∠BAC是不是弦切角?××××√·OABCDE如下图,已知AC与圆相切于点A,找出图中所有的弦切角及其所夹的弧。弦切角∠CAD夹的弧是AD⌒弦切角∠CAB夹的弧是ADB弦切角∠CAE夹的弧是ADE想一想 弦切角与圆上哪些相关角有关系?ABCDEABCDEABCDEABCDEABCDEABCDEAB(C)DE弦切角猜一猜 : ∠A= ∠BDE弦切角所夹弧所对的圆周角猜想:弦切角等于其所夹弧所对的圆周角圆周角定理的证明方法比一比: 分类讨论特殊到一般化归化归(1)圆心在圆周角内;(2)圆心在圆周角一边上;(3)圆心有圆周角外。ABEABEABEABEABEABEABEABEABE
(1)圆心在弦切角的外部;(2)圆心在弦切角的一边上; (3)圆心在弦切角的内部.由此发现,弦切角可分为三类:∴∠A=90°ABCE∟∵BC为直径,直径所对圆周角为直角又∵CE与圆相切,∴ ∠A= ∠BCE(1)当圆心在弦切角的一边上时: ∴BC⊥CE,∴∠BCE=90°弦切角弦切角所夹弧所对的圆周角(2)当圆心在弦切角外部时: ABCED化归∵∠DAC=∠DCE=90°且 ∠DAB=∠DCB∴∠BAC= 90°-∠DAB
= 90° -∠DCB = ∠BCE
∴∠BAC = ∠BCE∟∟弦切角弦切角所夹弧所对的圆周角(3)当圆心在弦切角内部时: ABCED化归∵∠DAC=∠DCE=90°且 ∠DAB=∠DCB∴∠BAC= 90°+ ∠DAB
= 90°+ ∠DCB = ∠BCE
∴∠BAC = ∠BCE弦切角弦切角所夹弧所对的圆周角 弦切角性质定理: 弦切角等于它所夹的弧对的圆周角.例1:如图,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D. 求证:AC平分∠BAD.O
ABCDE12要证AC平分∠BAD
即证∠1=∠2分析:可证这两角所在的直角三角形相似。 于是连结BC,得Rt△ACB 由弦切角性质 ∠ACD=∠B ,故结论得证∟O
ABCDE12解:连结BC∵ AD⊥CE, AB是⊙O的直径∴∠BCA=∠ADC=90°又∵CD与圆相切由弦切角性质∠ACD=∠ABC∴RT△ACB ~ RT△ADB∴∠1=∠2∴AC平分∠BADO
ABCDE12思路二: 连结OC 由切线性质,得OC⊥ED 从而OC∥AD 3于是有∠2=∠3 又由于∠1=∠3 从而有∠1=∠21、如右图,AB为⊙O的直径,
直线EF切⊙O于C,若∠BAC=56°
则∠ECA=_____度.2 、(07年广东高考文科选做题15).如下图所示,圆O 的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线L ,过A作L的垂线AD,垂足为D,则∠DAC=_____. 练一练:341230°∟分析:易知∠BAC+∠B=90°所以∠B= ∠ECA =34°∠ECA=∠B,分析:易知∠DAC+∠1=90°又∵∠1=∠2,易知△BCO为等边三角形∴ ∠1=∠2=60°∴∠DAC=30°练一练:如右图,经过⊙O上的点T的切线和弦AB的延长线相交于点C.求证:∠ATC=∠TBC.3、(课本 P34习题2.4第1题) 12解:由弦切角性质有∠1=∠2 又∵∠1+ ∠ATC = ∠2+ ∠TBC =180° ∴ ∠ATC=∠TBC方法一:方法二分析:由弦切角性质有
∠3=∠434而∠C=∠C所以△ACT~ △TCB 从而结论得证(相似三角形对应角相等)如图,经过⊙O上的点T的切线和弦AB的延长线相交于点C.求证:∠ATC=∠TBC.(1) 本节课主要学习的知识:弦切角定义及其性质定理(2)在学习过程中应用的
重要的数学思想方法: 分类讨论思想和化归思想作业课本P34
习题2.4第2题
谢谢! 如图,已知ABCD是圆的内接四边形,AB 是⊙O的
直径,MC切 ⊙O于C, ∠ BCM=32°,求∠B的度数。
补充题:32°(提示:弦切角等于其所夹弧所对圆心角的一半)
(1)圆心在弦切角的外部;(2)圆心在弦切角的一边上; (3)圆心在弦切角的内部.由此发现,弦切角可分为三类:∴∠A=90°ABCE∟∵BC为直径,直径所对圆周角为直角又∵CE与圆相切,∴ ∠A= ∠BCE(1)当圆心在弦切角的一边上时: ∴BC⊥CE,∴∠BCE=90°弦切角弦切角所夹弧所对的圆周角(2)当圆心在弦切角外部时: ABCED化归∵∠DAC=∠DCE=90°且 ∠DAB=∠DCB∴∠BAC= 90°-∠DAB
= 90° -∠DCB = ∠BCE
∴∠BAC = ∠BCE∟∟弦切角弦切角所夹弧所对的圆周角(3)当圆心在弦切角内部时: ABCED化归∵∠DAC=∠DCE=90°且 ∠DAB=∠DCB∴∠BAC= 90°+ ∠DAB
= 90°+ ∠DCB = ∠BCE
∴∠BAC = ∠BCE弦切角弦切角所夹弧所对的圆周角 弦切角性质定理: 弦切角等于它所夹的弧对的圆周角.例1:如图,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D. 求证:AC平分∠BAD.O
ABCDE12要证AC平分∠BAD
即证∠1=∠2分析:可证这两角所在的直角三角形相似。 于是连结BC,得Rt△ACB 由弦切角性质 ∠ACD=∠B ,故结论得证∟O
ABCDE12解:连结BC∵ AD⊥CE, AB是⊙O的直径∴∠BCA=∠ADC=90°又∵CD与圆相切由弦切角性质∠ACD=∠ABC∴RT△ACB ~ RT△ADB∴∠1=∠2∴AC平分∠BADO
ABCDE12思路二: 连结OC 由切线性质,得OC⊥ED 从而OC∥AD 3于是有∠2=∠3 又由于∠1=∠3 从而有∠1=∠21、如右图,AB为⊙O的直径,
直线EF切⊙O于C,若∠BAC=56°
则∠ECA=_____度.2 、(07年广东高考文科选做题15).如下图所示,圆O 的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线L ,过A作L的垂线AD,垂足为D,则∠DAC=_____. 练一练:341230°∟分析:易知∠BAC+∠B=90°所以∠B= ∠ECA =34°∠ECA=∠B,分析:易知∠DAC+∠1=90°又∵∠1=∠2,易知△BCO为等边三角形∴ ∠1=∠2=60°∴∠DAC=30°练一练:如右图,经过⊙O上的点T的切线和弦AB的延长线相交于点C.求证:∠ATC=∠TBC.3、(课本 P34习题2.4第1题) 12解:由弦切角性质有∠1=∠2 又∵∠1+ ∠ATC = ∠2+ ∠TBC =180° ∴ ∠ATC=∠TBC方法一:方法二分析:由弦切角性质有
∠3=∠434而∠C=∠C所以△ACT~ △TCB 从而结论得证(相似三角形对应角相等)如图,经过⊙O上的点T的切线和弦AB的延长线相交于点C.求证:∠ATC=∠TBC.(1) 本节课主要学习的知识:弦切角定义及其性质定理(2)在学习过程中应用的
重要的数学思想方法: 分类讨论思想和化归思想作业课本P34
习题2.4第2题
谢谢! 如图,已知ABCD是圆的内接四边形,AB 是⊙O的
直径,MC切 ⊙O于C, ∠ BCM=32°,求∠B的度数。
补充题:32°(提示:弦切角等于其所夹弧所对圆心角的一半)
