选修4-1 第二讲 直线与圆的位置关系弦切角的性质 课件 36张PPT
文档属性
| 名称 | 选修4-1 第二讲 直线与圆的位置关系弦切角的性质 课件 36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览


文档简介
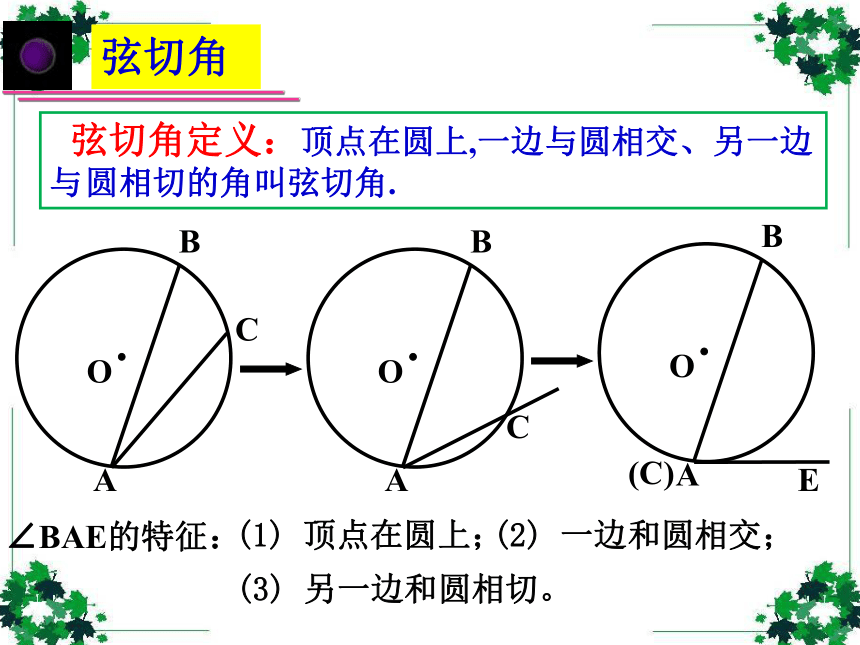
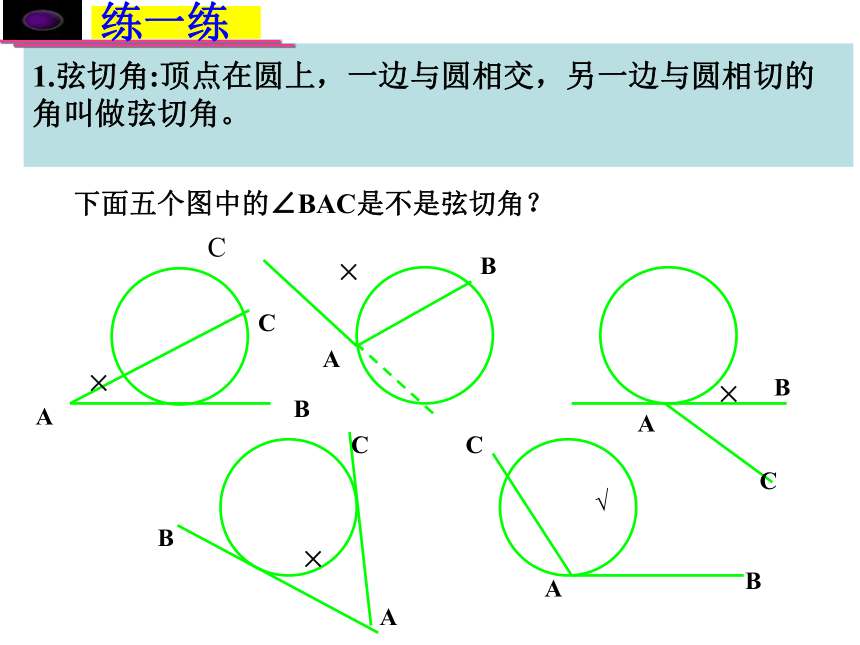
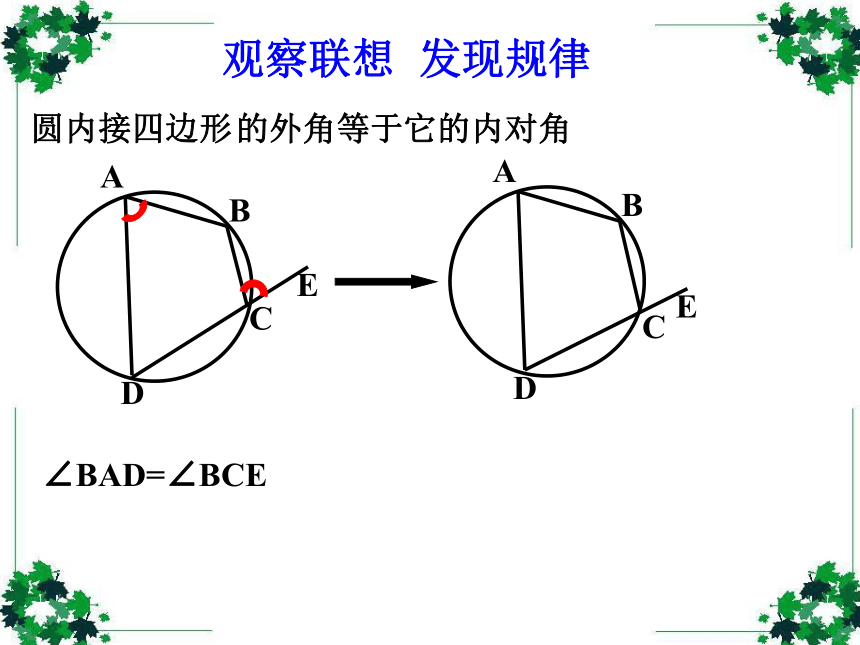
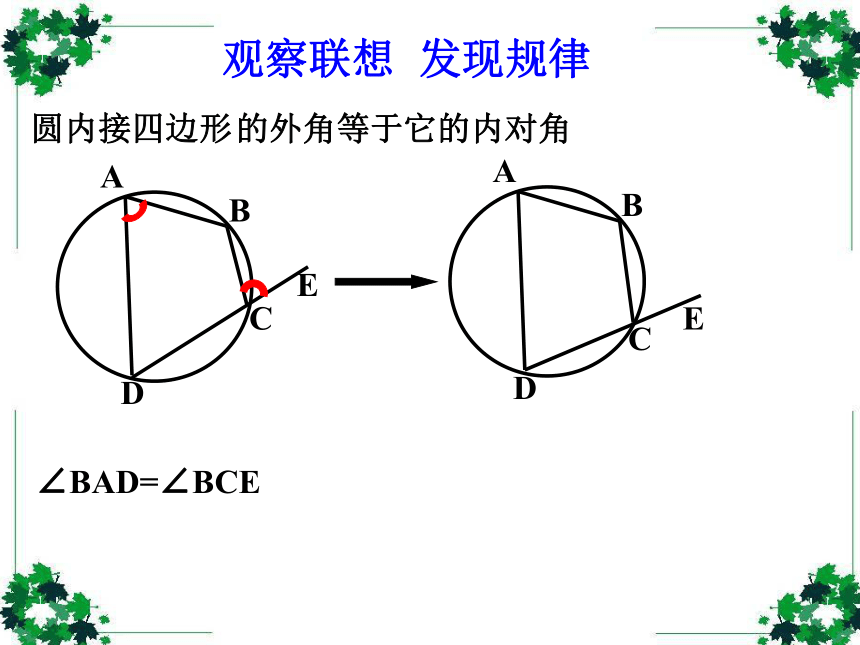
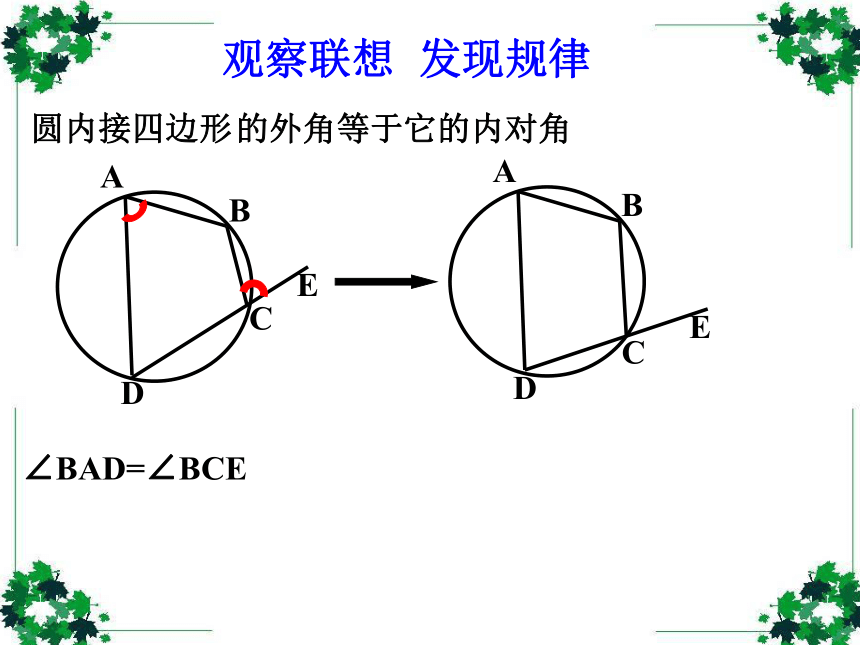
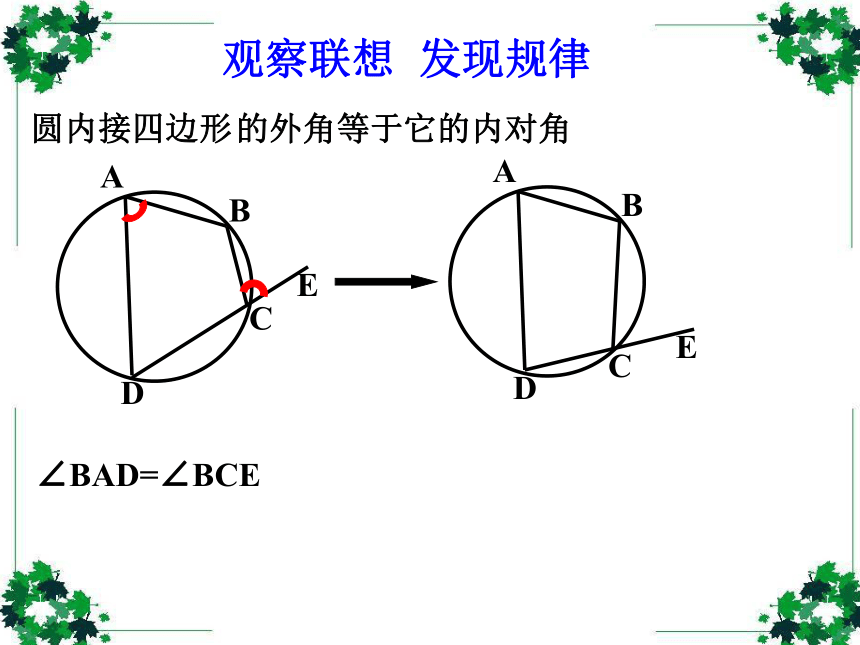
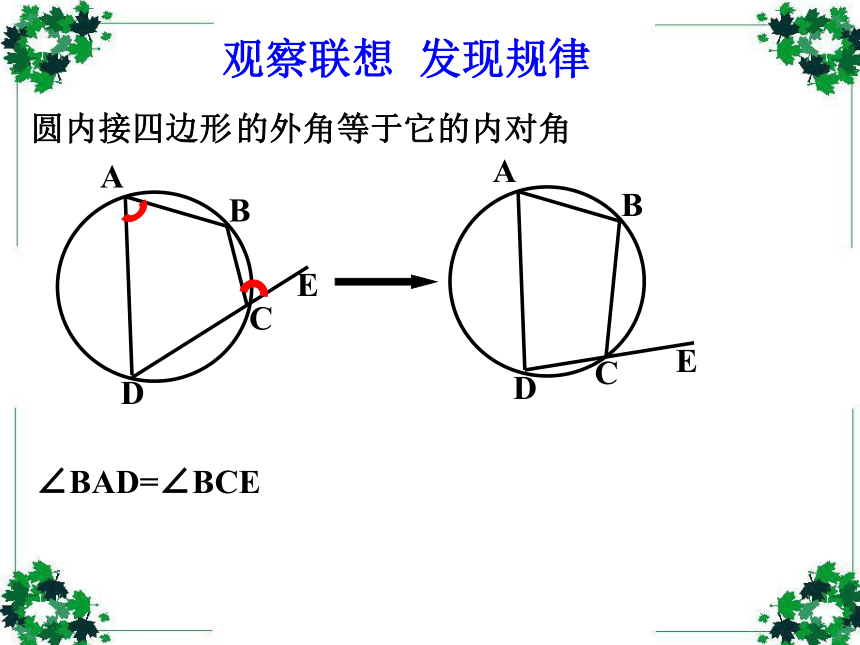
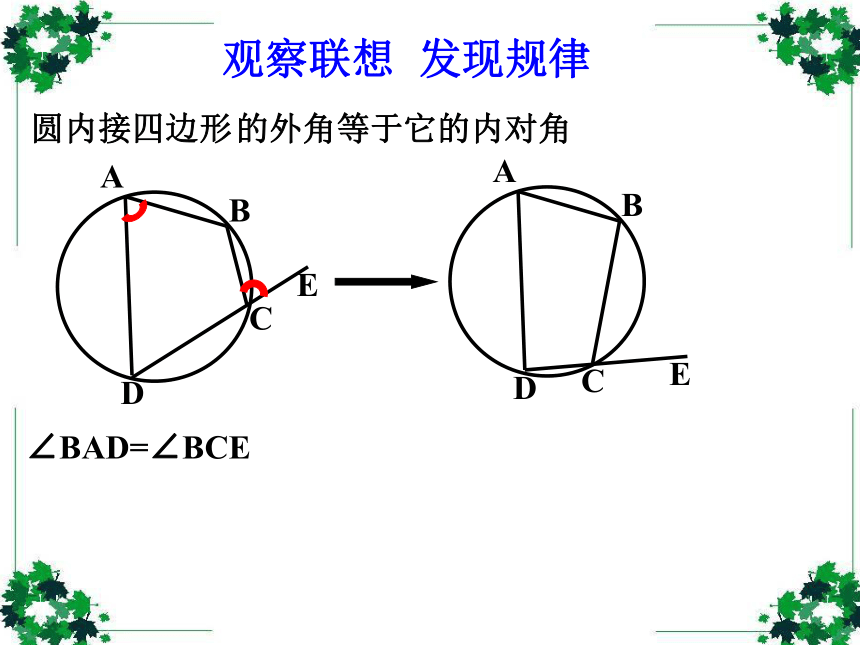
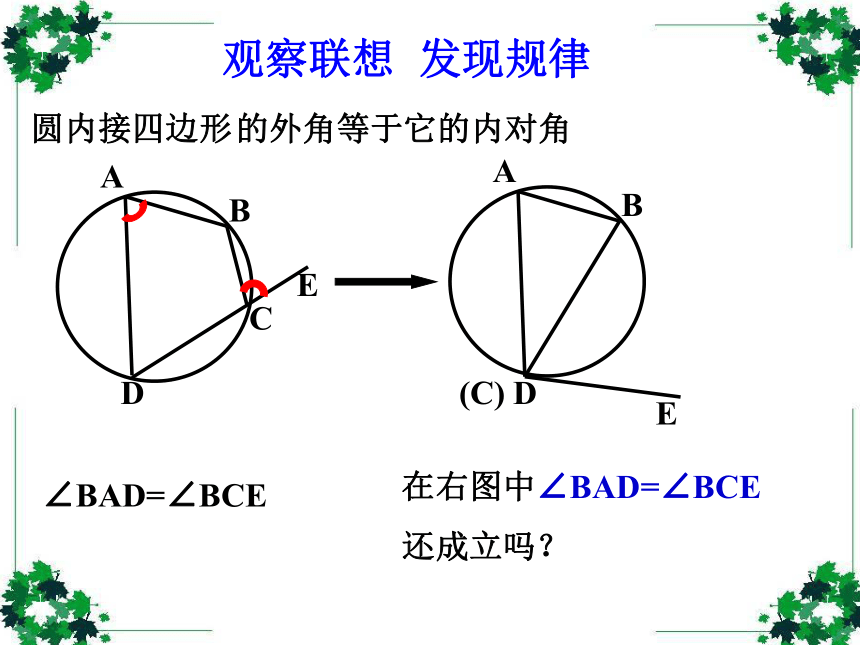
课件36张PPT。弦切角的性质创设情景 以旧探新 圆心角和圆周角 弦切角定义:顶点在圆上,一边与圆相交、另一边与 圆相切的角叫弦切角.(1) 顶点在圆上;(2) 一边和圆相交;(3) 另一边和圆相切。∠BAE的特征:AAAAABBBBBCCCCC下面五个图中的∠BAC是不是弦切角?××××√1.弦切角:顶点在圆上,一边与圆相交,另一边与圆相切的角叫做弦切角。圆内接四边形观察联想 发现规律∠BAD=∠BCE的外角等于它的内对角观察联想 发现规律观察联想 发现规律观察联想 发现规律观察联想 发现规律观察联想 发现规律观察联想 发现规律在右图中∠BAD=∠BCE
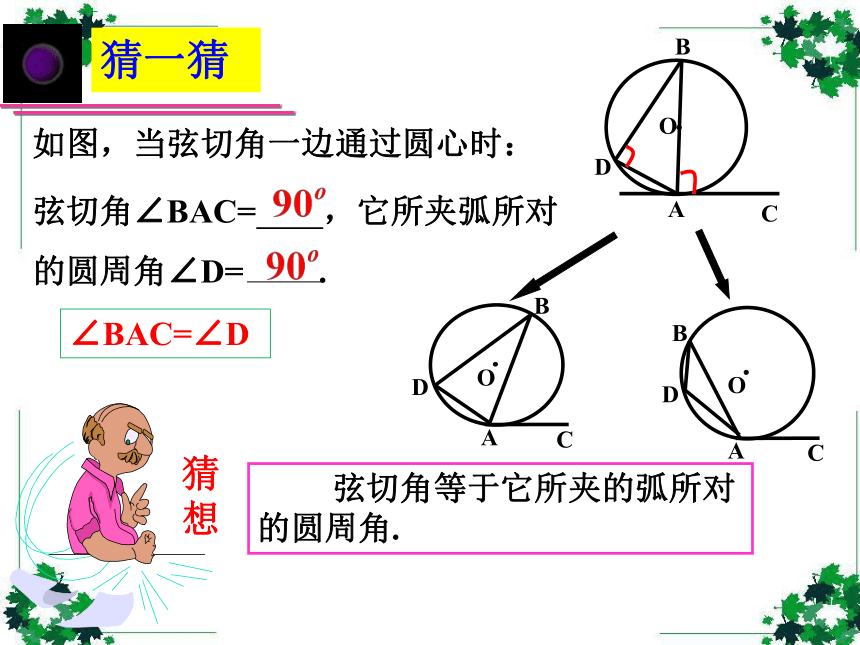
还成立吗?如图,当弦切角一边通过圆心时:弦切角∠BAC= ,它所夹弧所对
的圆周角∠D= . 弦切角等于它所夹的弧所对的圆周角.∠BAC=∠D类比联想 尝试论证圆周角定理的证明采用了什么方法?从特殊到一般的化归思想、分类讨论思想方法。尝试证明弦切角定理
弦切角等于它所夹的弧所对的圆周角.
几何语言:
若DE切圆于D,DB为弦,则∠BDE = ∠BAD (1).由上述定理的发现和证明过程可以看到,对一个图形进行适当的变化,往往能够发现几何中的一些有价值的结论.另外,猜想的证明渗透了:
①分类思想、②运动变化(特殊化)思想和③化归思想,你能从中体会这些思想方法吗? (2).弦切角定理的引入方法:采用了图形变化的方法,将内接四边形变化为它的极端情形,即三角形.由“圆内接四边形的外角等于它的内角的对角”去猜想“弦切角对于它所夹的弧对的圆周角”.已知AB是⊙O的切线,A为切点,由图填空: ∠1= ;∠2= ;∠3= ;∠4= 。30o70o65o40o巩固知识 初步应用例1.已知:如右图, AB是⊙O的直径, AC是弦,直线CE和⊙O切于点C, AD⊥CE,垂足为D.证明:AC平 分∠BAD。∵AB是⊙O的直径, ∴∠ACB=90°因此AC平分∠BAD。∴∠1=∠2∴∠ACD=∠B∵AC是弦,且CE和⊙O切于点C∴∠ACD+∠2=90°∵AD⊥CE ∴∠ ADC=90°∴∠B+∠1=90°解:连结BC巩固知识 初步应用例1.已知:如右图, AB是⊙O的直径, AC是弦,直线CE和⊙O切于点C, AD⊥CE,垂足为D.证明:AC平 分∠BAD。1、如图:AB为⊙O的直径,直线 EF
切于⊙O于C,若∠BAC=56°,则
∠ECA =_ 。2、如图,AB是⊙O 的直径,AC是弦,
直线CE和⊙O 切于点C,AD⊥CE,垂足
为D,若 ∠ACD = 400 ,则∠BAC= 。50o34o3、如图,经过⊙O上的点T的切线
和弦AB的延长线相交于点C。
说明: ∠ATC = ∠TBC课后小结1、弦切角的定义2、弦切角定理3、证明定理的思想方法(难点)作业布置:1、课本P34习题2.42、金榜 四、弦切角的性质再见谢谢指导!习题2.41.如图,经过圆上的点T的切线和弦AB的延长线相交于点C. 求证:∠ATC=∠TBC2.如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC·BDACTBwww.czsx.com.cn2、选择:
AB为⊙O直径,PC为⊙O的切线,C为切点,
若∠BPC=30°,则∠BCP=( )。
A、 30°B、 60°C、 15°D、22. 5°Awww.czsx.com.cn3,如图:四边形ABCD为圆内接四边形,AB 是直径,MN切⊙O于C点,∠BCM=38° 那么∠ABC的度数是( )。 A、38°B、52°C、68° D、42°38°BOABCMND例3、已知:BC与⊙O相切于点B,AF为⊙O的直径, CE⊥AF,垂足为E,求证:CD=CB 例4、AB为⊙O直径,PC为⊙O的切线,C为切点,若∠BPC=28o,求∠PCB的度数。 1.如图,AC是⊙O的弦,BD切⊙O于C,则图中弦切角有 个.4若∠AOC=1200,则∠ ACD = .6002.如图,直线MN切⊙O于C,AB是⊙O的直径,若∠ BCM=400,则∠ ABC等于( )A.400 B. 500 C. 450 D.6003.已知⊙O是△ABC的内切圆,D,E,F为切点,若∠ A: ∠ B: ∠ C=4:3:2, 则∠DEF = , ∠FEC= .B500700练习:∠ACD, ∠ACB, ∠OCD, ∠OCB.∵A=800,B=600,C=400.∴∠DOF=1000, ∴∠DEF=500 .∵C=400,CE=CF. ∴∠FEC=700 .4.由圆外一点B引圆的切线BA,切点为A,过点B引直线BC交圆于点C,D,若取BE=BA,求证:∠EAC=∠EAD.证明:∵ BE=BA,∴ ∠BAE=∠BEA.又∵ BA圆的切线,∴ ∠ BAC=∠ADC.而∵ ∠EAC=∠BAE- ∠BAC, 且 ∠EAD=∠BEA- ∠ADC.∴ ∠EAC=∠EAD .常用模型:
△BAC∽△BDA!5.EF切⊙O于点C,过弦AB的两端点A、B分别作AE⊥AB,BF⊥AB,OC交AB于点D.求证:(1)CE·CF=AD·DB;(2)CD2=AE·BF.证明:连结AC,BC.∵EF是⊙O 的切线,∴∠ECA=∠CBA, ∠FCB=∠CAB. 又∵ AE⊥AB,BF⊥AB,∴四点A,D,C,E共圆;四点A,D,C,E共圆; ∴ ∠ADC=∠CFB,
∴ △ADC∽△CFB .同理可得△ACE∽△CBD .6.如图,AB为⊙O的直径,BC 、CD为⊙O的切线, B 、D切点.求证:(1) AD//OC; (2)若⊙O 的半径等于1,求AD· OC 的值.证明:(1)∵BC 、CD是⊙O 的切线, B 、D切点.∴∠OBC=∠ODC=900. 又∵ OA=OD, ∴ ∠OAD=∠ODA.而∵ ∠BOD= ∠OAD+∠ODA=2 ∠OAD,
且 ∠BOD=2 ∠BOC.∴ ∠BOC=∠DOC.又∵OB=OD,OC=OC.∴ ∠OAD=∠BOC, ∴ AD//OC.∴Rt△OBC≌Rt△ODC.(2)连接BD, ∵ ∠OAD=∠BOC,∴Rt△OBC∽Rt△ADB.AAAAABBBBBCCCCC下面五个图中的∠BAC是不是弦切角?××××√1.弦切角:顶点在圆上,一边与圆相交,另一边与圆相切的角叫做弦切角。
还成立吗?如图,当弦切角一边通过圆心时:弦切角∠BAC= ,它所夹弧所对
的圆周角∠D= . 弦切角等于它所夹的弧所对的圆周角.∠BAC=∠D类比联想 尝试论证圆周角定理的证明采用了什么方法?从特殊到一般的化归思想、分类讨论思想方法。尝试证明弦切角定理
弦切角等于它所夹的弧所对的圆周角.
几何语言:
若DE切圆于D,DB为弦,则∠BDE = ∠BAD (1).由上述定理的发现和证明过程可以看到,对一个图形进行适当的变化,往往能够发现几何中的一些有价值的结论.另外,猜想的证明渗透了:
①分类思想、②运动变化(特殊化)思想和③化归思想,你能从中体会这些思想方法吗? (2).弦切角定理的引入方法:采用了图形变化的方法,将内接四边形变化为它的极端情形,即三角形.由“圆内接四边形的外角等于它的内角的对角”去猜想“弦切角对于它所夹的弧对的圆周角”.已知AB是⊙O的切线,A为切点,由图填空: ∠1= ;∠2= ;∠3= ;∠4= 。30o70o65o40o巩固知识 初步应用例1.已知:如右图, AB是⊙O的直径, AC是弦,直线CE和⊙O切于点C, AD⊥CE,垂足为D.证明:AC平 分∠BAD。∵AB是⊙O的直径, ∴∠ACB=90°因此AC平分∠BAD。∴∠1=∠2∴∠ACD=∠B∵AC是弦,且CE和⊙O切于点C∴∠ACD+∠2=90°∵AD⊥CE ∴∠ ADC=90°∴∠B+∠1=90°解:连结BC巩固知识 初步应用例1.已知:如右图, AB是⊙O的直径, AC是弦,直线CE和⊙O切于点C, AD⊥CE,垂足为D.证明:AC平 分∠BAD。1、如图:AB为⊙O的直径,直线 EF
切于⊙O于C,若∠BAC=56°,则
∠ECA =_ 。2、如图,AB是⊙O 的直径,AC是弦,
直线CE和⊙O 切于点C,AD⊥CE,垂足
为D,若 ∠ACD = 400 ,则∠BAC= 。50o34o3、如图,经过⊙O上的点T的切线
和弦AB的延长线相交于点C。
说明: ∠ATC = ∠TBC课后小结1、弦切角的定义2、弦切角定理3、证明定理的思想方法(难点)作业布置:1、课本P34习题2.42、金榜 四、弦切角的性质再见谢谢指导!习题2.41.如图,经过圆上的点T的切线和弦AB的延长线相交于点C. 求证:∠ATC=∠TBC2.如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC·BDACTBwww.czsx.com.cn2、选择:
AB为⊙O直径,PC为⊙O的切线,C为切点,
若∠BPC=30°,则∠BCP=( )。
A、 30°B、 60°C、 15°D、22. 5°Awww.czsx.com.cn3,如图:四边形ABCD为圆内接四边形,AB 是直径,MN切⊙O于C点,∠BCM=38° 那么∠ABC的度数是( )。 A、38°B、52°C、68° D、42°38°BOABCMND例3、已知:BC与⊙O相切于点B,AF为⊙O的直径, CE⊥AF,垂足为E,求证:CD=CB 例4、AB为⊙O直径,PC为⊙O的切线,C为切点,若∠BPC=28o,求∠PCB的度数。 1.如图,AC是⊙O的弦,BD切⊙O于C,则图中弦切角有 个.4若∠AOC=1200,则∠ ACD = .6002.如图,直线MN切⊙O于C,AB是⊙O的直径,若∠ BCM=400,则∠ ABC等于( )A.400 B. 500 C. 450 D.6003.已知⊙O是△ABC的内切圆,D,E,F为切点,若∠ A: ∠ B: ∠ C=4:3:2, 则∠DEF = , ∠FEC= .B500700练习:∠ACD, ∠ACB, ∠OCD, ∠OCB.∵A=800,B=600,C=400.∴∠DOF=1000, ∴∠DEF=500 .∵C=400,CE=CF. ∴∠FEC=700 .4.由圆外一点B引圆的切线BA,切点为A,过点B引直线BC交圆于点C,D,若取BE=BA,求证:∠EAC=∠EAD.证明:∵ BE=BA,∴ ∠BAE=∠BEA.又∵ BA圆的切线,∴ ∠ BAC=∠ADC.而∵ ∠EAC=∠BAE- ∠BAC, 且 ∠EAD=∠BEA- ∠ADC.∴ ∠EAC=∠EAD .常用模型:
△BAC∽△BDA!5.EF切⊙O于点C,过弦AB的两端点A、B分别作AE⊥AB,BF⊥AB,OC交AB于点D.求证:(1)CE·CF=AD·DB;(2)CD2=AE·BF.证明:连结AC,BC.∵EF是⊙O 的切线,∴∠ECA=∠CBA, ∠FCB=∠CAB. 又∵ AE⊥AB,BF⊥AB,∴四点A,D,C,E共圆;四点A,D,C,E共圆; ∴ ∠ADC=∠CFB,
∴ △ADC∽△CFB .同理可得△ACE∽△CBD .6.如图,AB为⊙O的直径,BC 、CD为⊙O的切线, B 、D切点.求证:(1) AD//OC; (2)若⊙O 的半径等于1,求AD· OC 的值.证明:(1)∵BC 、CD是⊙O 的切线, B 、D切点.∴∠OBC=∠ODC=900. 又∵ OA=OD, ∴ ∠OAD=∠ODA.而∵ ∠BOD= ∠OAD+∠ODA=2 ∠OAD,
且 ∠BOD=2 ∠BOC.∴ ∠BOC=∠DOC.又∵OB=OD,OC=OC.∴ ∠OAD=∠BOC, ∴ AD//OC.∴Rt△OBC≌Rt△ODC.(2)连接BD, ∵ ∠OAD=∠BOC,∴Rt△OBC∽Rt△ADB.AAAAABBBBBCCCCC下面五个图中的∠BAC是不是弦切角?××××√1.弦切角:顶点在圆上,一边与圆相交,另一边与圆相切的角叫做弦切角。
